My Other Math Sites
Lessons From the Classroom
A Tale of Two Gyms
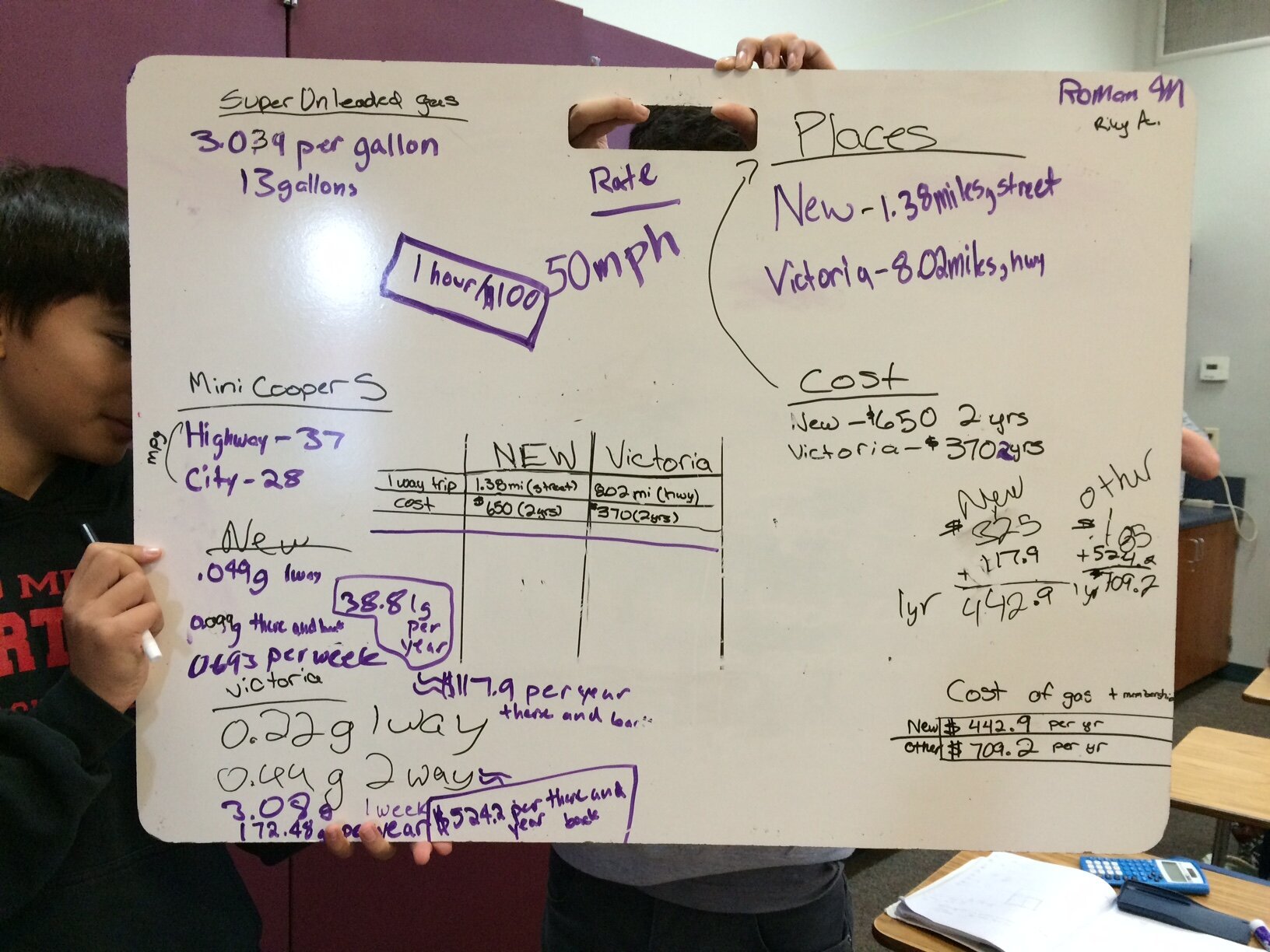
Quick post about a scenario that I was sharing with the kids just to share and how they just took off with it. A brand spanking new 24-Hour Fitness is opening up near me. It's a no-brainer to switch over to this facility because I'll save gas and travel time. However, the 2-year membership that I get from Costco will cost nearly twice as much at the new one. I gave them some information:
8.02 miles one-way to current gym, at mostly highway speed
1.38 miles one-way to new gym, at neighborhood speed
Chevron gasoline currently at $3.039/gallon
$370/2-year membership at current gym
$650/2-year membership at new gym
While it didn't take much to figure out that the new gym costs just 38 cents more per day, but there were enough variables inherent in this scenario that the kids wanted to take a closer look.They asked me questions like:
How often do you go to the gym?
How much mileage does your car get?
How fast do you drive — on highway and around town?
How long does it take you?
I lied about going to the gym 7 days a week, gave them my car model, then told them to look up the rest. But then we wondered about the value of my time driving. How much is my driving time worth? I went on Twitter to ask for help, and Glenn thought I should divide my weekly salary by the hours of weekly driving that I do. The problem is I live pretty close to school, so this rate becomes too high to apply to this situation. For no good reason, I decided to give the kids our school's substitute rate of $115/7 hours, or $16.43/hour. They paired up and went online to gather more information, did a bunch of calculations, and summarized everything on the whiteboard. All in one class period.We should just do this all year: turn a scenario into a question then into a math task. I could take a nap while they chitchat and do all the work.
Four Square and Other Questions
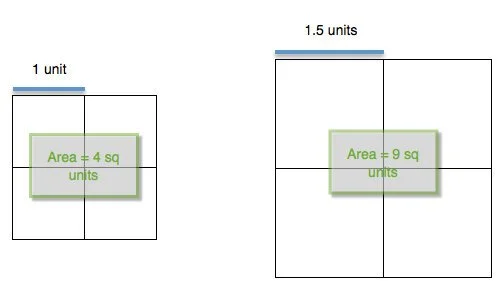
One afternoon during recess I noticed that the Four Square grid at our school had been enlarged. Naturally I yelled out to the kids, "Hey kids, when did they make this larger? I wonder what percent increase this is. What do you think?”
Taking a nanosecond pause from their game, they yelled out their estimates, anywhere from 50% to 95% increase. One kid said, "I love that you're asking us a math question at recess time." I went back out to the playground during my prep with a couple of yardsticks to find the answer to the question I'd posed. When my 6th graders came into class the next period, I told them what I'd wondered about during recess and wanted each one of them to give me an estimate of this percent increase. We walked back out to the Four Square, and I allowed them five minutes to do whatever they needed to get a good estimate.
Once back into the classroom, I asked them to write down their estimate of the percent increase on a small slip of paper. I then asked, "What exactly was I looking for? Percent increase in what? I really didn't say and you didn't ask me to specify either."
We've been working A LOT with perimeter and area of rectangles, so most of them said that they'd thought I'd meant the percent increase in area. So I told them I did mean area but I was intentionally vague just to see if anyone would ask — and Four Square is so much about occupying the inside space. This question prompted me to ask them more questions about increase in perimeter versus increase in area. I had them draw squares (or rectangles) on grid paper and explore the changes in area when the perimeter is doubled, tripled, or by some x factor. We remind ourselves that area is two-dimensional and why area units are always "squared." I asked them how they would figure out the percent increase in area. They told me I needed to measure the length and width of the old Square (black outlines), then do the same for the new one (white outlines). They also agreed that I could just find the area of 1 square, then multiply this by 4 to get the whole thing. This suggestion prompted me to ask them, "Well, do I need to compare the area of the whole 4-square grid of new to old, or just the area of 1-square of new to old?" So we just drew some squares to show that comparing the areas of just one square each: large to small is 2.25 to 1.0, this is a percent increase of 125%. And comparing the areas of each entire 4-square grid: large to small is 9 to 4, which also yields a 125% increase.
This brief noticing and wondering yielded a fruitful discussion and it was something that was part of their environment, their playground. By the way, the answer is 118% increase in area for the Four Square. The closest written estimate was 115%. Of course this launched us into a brainstorming session of questions that they have about their surroundings. Stuff that we can apply math to answer the questions. I reminded them not to worry about answering the question. Just ask it. Then I couldn't stop them from sharing. (These 6th graders are away at Outdoor School, so I have to wait for them to return next week for us to try and answer some of these questions. They will also be jotting down more questions that may come up during the week.)
How much time does my brother waste in his room for a year?
How many gallons of water do we use if we take 5-minute showers a day?
How much does this cost?
How much power is needed to charge all the devices in the house for a year?
I wonder how many pencil tips I break each year, and if added end-to-end, how long would this be?
What is the average amount of money each teacher at our school spends on supplies in a school year
How many eggs does a chicken lay in United Kingdom?
How much pollution does the average car put into the air monthly?
How much time do the students in this class spend on YouTube in a month?
How much time do we spend on homework during the school year?
How much money does our school lose when students are absent?
How long does my hair grow in a month?
I always wondered how much bigger is the big basketball hoop compared to the small one.
How many pounds of food do kids waste in the cafeteria in a month?
How much gas does my mom burn while she is driving?
I wonder how much gasoline our 3 school buses use each year.
How many "perimeters" do we do in a year in PE?
How much money does Mrs. Nguyen spend on Oregon Ducks' games?...
And this one breaks my heart.
How long would it take to end poverty?
Driving Them Nuts
I'm proud of my students. I'm proud of what we do in room 15. My classroom. My home away from home for the last 11 years. These bopping teenagers, sullen one minute bubbly the next, hormonal but invincible. They don't all love math like I do. (Not everyone loves college football, but we get along.)
What is happening in room 15 is the loud and proud math culture that we have set in place. We build it from day one — then we continue to do, say, and write stuff to sustain and strengthen the culture because we know our behaviors are our best evidence that this culture exists.
Here's one piece of that evidence:
Her frustration resulted in her loving the problem. Her last sentence is an enormous celebration of how much we honor the process of problem solving. Her classmates had their own reflections — short snippets of how they engaged in the problem.
They worked hard on the problem because it was driving them nuts. It's not unusual to hear kids blurt out, "This problem is making me crazy!" Or, "I won't be able to think about anything else until I get this!" Now, they've owned it. This isn't about a letter grade any more; and it certainly isn't about me.
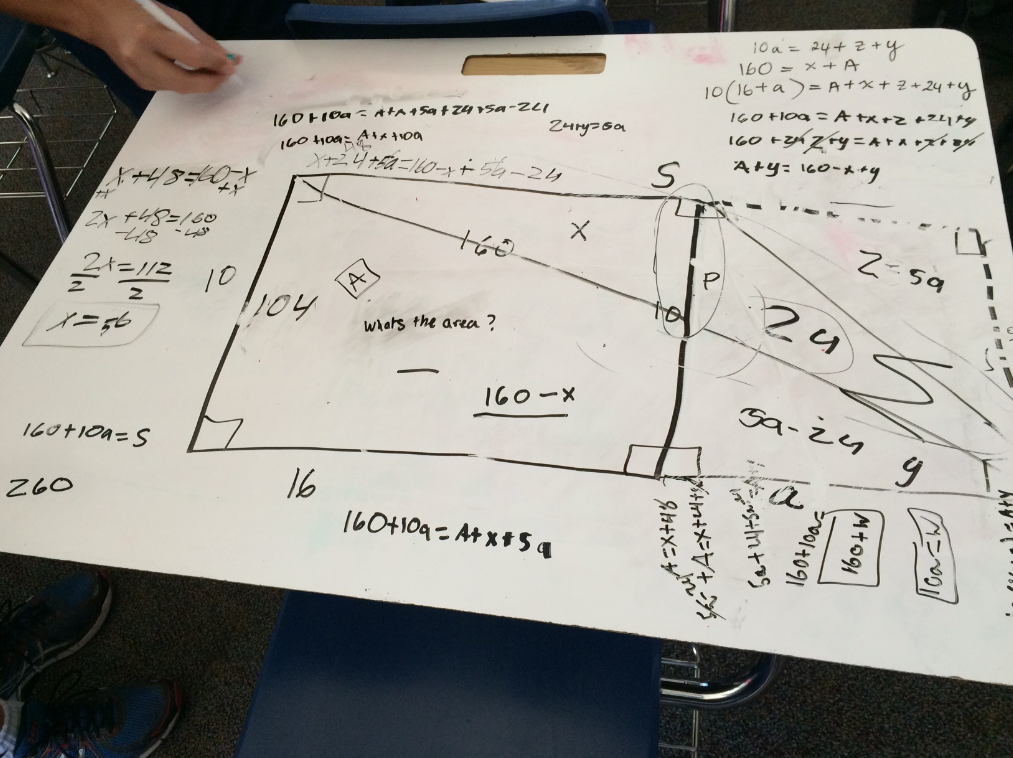
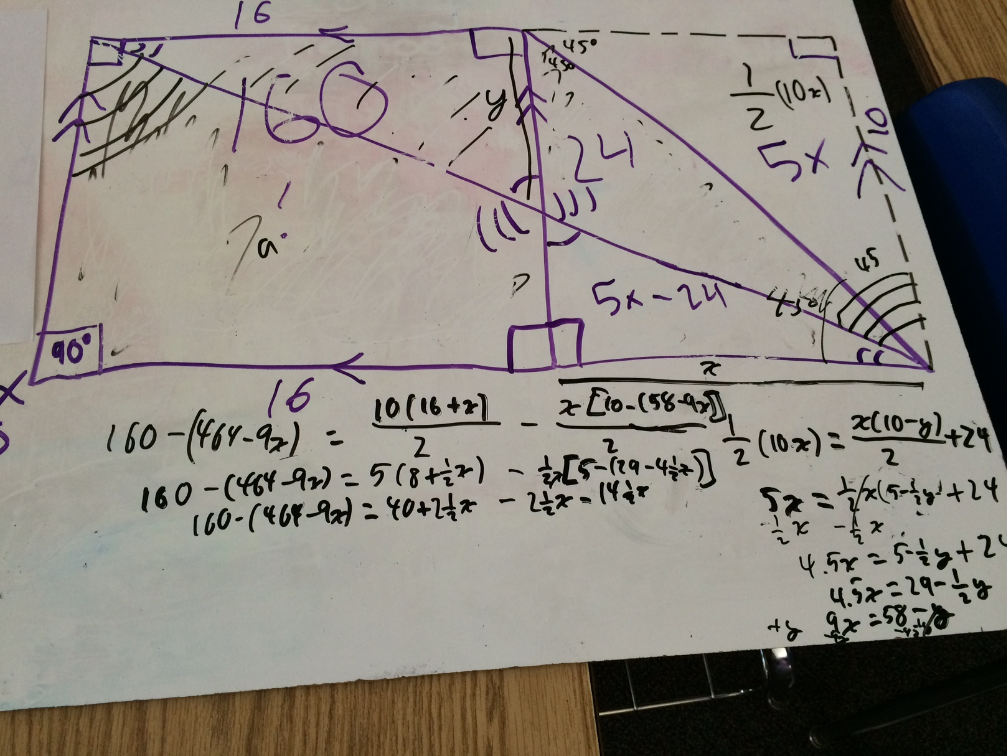
This was the problem they'd worked on.
The Missing Area
A 10 by 16 rectangle is attached to a triangle as shown below. If the purple section is 24 square units, then what is the area of the yellow section of the rectangle?
John Golden, GeoGebra extraordinaire, created an animated gif of this problem.
Mike Lawler solved this problem using similar triangles.
A Simpler Solution
I'm guessing this was about 5 years ago. I was at an all-day workshop when a high school math teacher, sitting next to me, asked about the PoW (from mathforum.org) that I had assigned to my students. I happened to have an extra copy in my backpack and gave it to her.
Dad's Cookies [Problem #2959]
Dad bakes some cookies. He eats one hot out of the oven and leaves the rest on the counter to cool. He goes outside to read.
Dave comes into the kitchen and finds the cookies. Since he is hungry, he eats half a dozen of them.
Then Kate wanders by, feeling rather hungry as well. She eats half as many as Dave did.
Jim and Eileen walk through next, each of them eats one third of the remaining cookies.
Hollis comes into the kitchen and eats half of the cookies that are left on the counter.
Last of all, Mom eats just one cookie.
Dad comes back inside, ready to pig out. "Hey!" he exclaims, "There is only one cookie left!"
How many cookies did Dad bake in all?
Maybe you'd like to work on this problem before reading on.
…
…
…
…
…
…
The teacher started solving the problem. She was really into it, so much so that I felt she'd ignored much of what our presenter was presenting at the time. She ran out of paper and grabbed some more. She looked up from her papers at one point and said something that I interpreted as I-know-this-problem-is-not-that-hard-but-what-the-fuck.
It was now morning break.
She worked on it some more.
By lunch time, she asked, "Okay, how do you solve this?" I read the problem again and drew some boxes on top of the paper that she'd written on. (Inside the green.)
She knew I'd solved the problem with a few simple sketches because she understood the drawings and what they represented. I just really appreciated her perseverance.
I share this with you because a few nights ago I was at our local Math Teachers' Circle where Joshua Zucker led us through some fantastic activities with Zome models. We were asked for the volume of various polyhedrons relative to one another. Our group really struggled on one of the shapes. We used formulas and equations only to get completely befuddled, and our work ended up looking like one of the papers above.
Over the years I've heard a few students tell me, "Mrs. Nguyen, my uncle is an engineer, and he can't help me with the PoW." Substitute uncle with another grown-up family member. Substitute engineer with another profession, including math teacher. I remember getting a note from one of my student's tutor letting me know that I shouldn't be giving 6th graders problems that he himself cannot solve. (The student's parent fired him upon learning this.)
I like to think that my love of problem solving will rub off on my kids. I hope they will love the power of drawing rectangles as much I do.
Multiplication: Finding the Greatest Product
From a set of 1 through 9 playing cards, I draw five cards and get cards showing 8, 4, 2, 7, and 5. I ask my 6th graders to make a 3-digit number and a 2-digit number that would yield the greatest product. I add, "But do not complete the multiplication — meaning do not figure out the answer. I just want you to think about place value and multiplication."
I ask for volunteers who feel confident about their two numbers to share. This question brings out more than a few confident thinkers — each was so confident that he/she had the greatest product. (I'm noting here that I wasn't entirely sure what what the largest product would be. After this lesson, I asked some math teachers this question, and I appreciate the three teachers who shared. None of them gave the correct answer.)
I say, "Well, this is quite lovely, but y'all can't be right." I ask everyone to look at the seven "confident" submissions and see if they could reason that one yields a greater product than another, then perhaps we might narrow this list down a bit.
Someone sees "easily" that #7 is greater than #6. The class agrees.
Someone says #7 is greater than #1 because of "doubling." She says, "I know this from our math talk. Doubling and halving. Look at #1. If I take half of 875, I get about 430. If I double 42, I get 84. Both of these numbers [430 and 84] are smaller than what are in #7. So I'm confident #7 is greater than #1."
Someone else says #5 is greater than #4 because of rounding, "Eight hundred something times 70 is greater than eight hundred something times 50. The effect of multiplying by 800 is much more."
Someone says, "Number 2 is also greater than #1 because of place value. I mean the top numbers are almost the same, but #2 has twelve more groups of 872."
But the only one that the class unanimously agrees on to eliminate is #6. Then I ask them to take 30 seconds to quietly examine the remaining six and put a star next to the one that they believe yield the greatest product. These are their votes.
I tell them that clearly this is a tough thing to think about because we've had a lot of discussion yet many possibilities still remain. And that's okay -- that's why we're doing this. We've been doing enough multiplication of 2-digit by 2-digit during math talks that it's time we tackle something more challenging. So #3 gets the most votes.
I then punch the numbers into the calculator, and the kids are very excited to see what comes up after each time that I hit the ENTER key. Cheers and groans can be heard from around the room. Turns out #3 does has the greatest product (63,150) out of the ones shown.
Ah, but then someone suggests 752 times 84. I punch it into the calculator and everyone gasps. It has a product of 63,168.
Their little heads are exploding.
I give them a new set of five for homework: 2, 3, 5, 6, and 9. They are to go home and figure out the largest product from 3-digit by 2-digit multiplication. They come back with 652 times 93.
The next day, we try another set: 3, 4, 5, 8, and 9. We get the greatest product by doing 853 times 94. There is a lot — as much if not more than the day before — of sharing and arguing and reasoning about multiplication and place value.
Many of them see a pattern in the arrangement of the digits and are eager to share. They've agreed on this placement.
Then we talk about making sure we know we've looked at all the possible configurations. They agree that the greatest digit has to either be in the hundreds place of the 3-digit number or in the tens place of the 2-digit number. We try a simple set of numbers 1 through 5, and we agree that there are just 9 possible candidates that we need to test. The same placement holds.
Then we draw generic rectangles to remind us that we've just been looking for two dimensions that would give us the largest area.
I remember saying to the class, more than once, that this is tough to think about. To which Harley, sitting in the front row, says, "But it's like we're playing a game. It's fun."
Two Pizzas and Five People
I'm thinking a lot about how my 6th graders responded to a pre-lesson task in "Interpreting Multiplication and Division" — a lesson from Mathematics Assessment Project (MAP) .
MAP lessons begin with a set structure:
Before the lesson, students work individually on a task designed to reveal their current levels of understanding. You review their scripts and write questions to help them improve their work.
I gave the students this pre-lesson task for homework, and 57 students completed the task.
I'm sharing students' responses to question 2 (of 4) only because there's already a lot here to process. I'm grouping the kids' calculations and answers based on their diagrams.
Each pizza is cut into fifths.
About 44% (25/57) of the kids split the pizzas into fifths. I think I would have done the same, and my hand-drawn fifths would only be slightly less sloppy than theirs. The answer of 2 must mean 2 slices, and that makes sense when we see 10 slices total. The answer 10 might be a reflection of the completed example in the first row. "P divided by 5 x 2 or 5 divided by P x 2" suggests that division is commutative, and P here must mean pizza.
Each pizza is cut into eighths.
Next to cutting a circle into fourths, cutting into eighths is pretty easy and straightforward.
Each pizza is cut into tenths.
I'm a little bit surprised to see tenths because it's tedious to sketch them in, but then ten is a nice round number. The answer 20, like before, might be a mimic of the completed example in the first row.
Each pizza is cut into fourths.
I'm thinking the student sketched the diagram to illustrate that the pizzas get cut into some number of pieces — the fourths are out of convenience. The larger number 5 divided by the smaller number 2 is not surprising.
Each pizza is cut into sixths.
It's easier to divide a circle by hand into even sections, even though the calculations do not show 6 or 12.
Each pizza is cut into fifths, vertically.
Oy. I need to introduce these 3 students to rectangular pizzas. :)
Five people? Here, five slices.
Mom and Dad are bigger people, so they should get the larger slices. This seems fair. We just need to examine the commutative property more closely.
Circles drawn, but uncut.
I'm wondering about the calculation of 5 divided by 2.
Only one pizza drawn, cut into fifths.
Twenty percent fits with the diagram, if each person is getting one of the five slices. The 100 in the calculation might be due to the student thinking about percentage.
Only one pizza drawn, cut into tenths, but like this.
I wonder if the student has forgotten what the question is asking for because his/her focus has now shifted to the diagram.
Each rectangular pizza is cut into fifths.
Three kids after my own heart.
Five portions set out, each with pizza sticks.
I wonder where the 10 comes from in his calculation.
Five plates set out, each plate with pizza slices.
Kids don't always know what we mean by "draw a picture" or "sketch a diagram." This student has already portioned out the slices.
What diagrams and calculations would you expect to see for question 3?
There's important work ahead for us. The kids have been working on matching calculation, diagram, and problem cards. They're thinking and talking to one another. I have a lot of questions to ask them, and hopefully they'll come up with questions of their own as they try to make sense of it all. If I were just looking for the answer of 2/5 or 0.4, then only 12 of the 57 papers had this answer. But I saw more "correct" answers that may not necessarily match the key. We starve ourselves of kids' thinking and reasoning if we only give multiple-choice tests or seek only for the answer.
That's why Max Ray wants to remind us of why 2 > 4.
The Number Sense by Stanislas Dehaene
I heavily skimmed the middle parts of this book when I bought it in May 2012. [Thanks to Christopher Danielson for recommending it.]
I’m re-reading some parts now, and the sub-section Teaching Number Sense [pages 124 – 128] resonates with me, not just in elementary school mathematics, but in K-12 mathematics.
If my hypothesis is correct, innumeracy is with us for a long time, because it reflects one of the fundamental properties of our brain: its modularity, the compartmentalization of mathematical knowledge within multiple partially autonomous circuits… The numerical illiterate performs calculations by reflex, haphazardly and without any deep understanding.
… A good teacher is an alchemist who gives a fundamentally modular human brain the semblance of an interactive network. Unfortunately our schools often do not quite meet this challenge. All too often, far from smoothing out the difficulties raised by mental calculation, our educational system increases them… But our schools are often content with inculcating meaningless and mechanical arithmetical recipes into children.
This state of affairs is all the more regrettable because… most children enter preschool with a well-developed understanding of approximation and counting. In most math courses, this informal baggage is treated as a handicap rather than as an asset. Finger counting is considered a childish activity that a good education will quickly do away with. How many children try to hide when they count on their fingers because “the teacher said not to”?
Despising children’s precocious abilities can have a disastrous effect on their subsequent opinion of mathematics.
… It seems more likely that many of these “mathematically disabled” children are normally abled pupils who got off to a false start in mathematics. Their initial experience unfortunately convinces them that arithmetic is a purely scholastic affair, with no practical goal and no obvious meaning. They rapidly decide that they will never be able to understand a word about it. The already considerable difficulties posed by arithmetic to any normally constituted brain are thus compounded by an emotional component, a growing anxiety or phobia about mathematics.
… We need to help children realize that mathematical operations have an intuitive meaning, which they can represent using their innate sense of numerical quantities. In brief, we must help them build a rich repertoire of “mental models” of arithmetic… The day the teacher introduces negative numbers and asks pupils to compute 3 – 9, a child who only masters the set scheme judges this operation impossible. Taking 9 apples from 3 apples? That’s absurd! Another child who relies exclusively on the distance scheme concludes that 3 – 9 = 6, because indeed the distance from 3 to 9 is 6. If the teacher merely maintains that 3 – 9 equals “minus six,” the two children run the risk of failing to understand the statement. The temperature scheme, however, can provide them with an intuitive picture of negative numbers. Minus six degrees is a concept that even first-graders can grasp.
But let us leave this chapter with a note of optimism… In the United States, the national council of teachers of mathematics is now de-emphasizing the rote learning of facts and procedures and is focusing instead on teaching an intuitive familiarity with numbers… Number sense — indeed, common sense — is making a comeback.
In fact, most children are only too pleased to learn mathematics if only one shows them the playful aspects before the abstract symbolism. Playing snakes and ladders may be all children need to get a head start in arithmetic.
By the way, I don’t read this and put the blame entirely on myself and my colleagues. As long as we place more emphasis on test scores than we do on learning, we are at best hypocrites.
Pacing Guide
For someone who has openly admitted to not following curriculum pacing guides, I sure spent a ridiculous amount of time churning one out. Our middle school is adopting CPM Core Connections 1, 2, and 3. Aside from our own reviews, the decision to go with CPM were also based on:
Desmos is embedded in many lessons
Other teachers' reviews, including Riley Lark's
I don't know if this would be of any use to you, but I might as well share the doc math 8 pacing 2014-2015. It's kinda pretty.
I replicate our school calendar and put in all the holidays and half-days. I go to each chapter in CPM and write down the guiding questions. Matching up the standards to each chapter was a pain in the ass. (CPM does it the other way around: they have the standards in one column and the different lessons that cover those standards in another.) The suggested number of days for each chapter does not include assessments, so I add about 6 days on top of whatever CPM recommended. I'm going to post the pacing guide near my desk — probably the only document I will print in full color this school year.
(Oh, I took out Chapter 1 because it's on problem solving. C'mon, I got this.)
Then I'm going supplement it like crazy. I can't teach straight from the textbook. Just can't. So the 6 days that I add to each chapter will hopefully allow us some wiggle room to do other stuff.
Other stuff includes, but not limited to, what you see on the right sidebar of my blog.
We also need time to begin each class period with math talks because it was one of the most powerful things we did last year. (Grrrrr. Just realized that most of the images on the math talks site are not there. Why now.)
I was brainstorming with a couple of 6th grade math teachers at another district, and we were listing out a possible warm-up/math talk schedule, something like:
Monday: number talk (spreadsheet that you can take from and add to)
Tuesday: visual pattern
Wednesday: estimation 180
Thursday: fun fact, or WYR, or Keeping Skills Sharp, or SBAC/review question
Friday: personal reflection
My assignment this year looks almost like last year's: 2 sections of Math 6, 1 section of Math 8, and 1 section of Geometry [1].
I wish you a healthy school year. Teach what you love and love the kids. Follow the rules, but break a few if doing so makes it better for the kids.
[1] I'm happy to say that we will no longer be tracking kids in math. However, we need to finish out what we'd started with these 8th graders who took Algebra last year as 7th graders. So this group will do some geometry, some stats, and a whole lot of problem solving.
Come and Observe
I don’t know what else to do except to suggest to an anti-Common Core parent to come and visit my classroom. Visit for a period or stay for the day. Come back again the next day. Stay for a week. Come back again next month. Become a parent volunteer in my room. Help me help a child because God knows we all have children in our room who could use some one-on-one support.
Parents should be our allies. A few are crazy. But there are a few teachers, doctors, plumbers, postal workers who are crazy too. Parents love their kids and want what’s best for them. They are concerned that their kids won’t be developmentally ready for Common Core (CC). They fear that it’s one-size-fits-all, that CC controls kids’ minds and stifle their creativity, that national testing and national curriculum will soon follow. The list of concerns just keeps piling up.
Both sides are quite passionate and create a lot of noise. I engage very little in this noise because I feel my energy in doing so does not get converted into anything useful. It dissipates too quickly, leaving me hollow and out of breath. But I’m talking now by writing. It’s midnight and really quiet here.
I want parents to observe their children do Taco Cart and Always, Sometimes, and Never. I want them to listen in on the kids’ math talks. I want them to walk in on a day when I’m doing direct instruction — and observe how much the kids direct their own learning, how much they try to make sense of something new.
I want parents to observe you — my local and online colleagues whose lessons I steal from and whose support only makes me work harder.
So, that’s my plan. I will invite my parents to visit my classroom whenever they want (I actually prefer unannounced) and see how a CC lesson plays out. The worst that can happen is I fail miserably. But I guarantee their kid will not.
I found some very old arithmetic textbooks, dating back to the 1800’s at Open Library.
Bonnycastle, John. Arithmetic… 17th ed. London: Longman, 1843. Print
These prefaces are quite remarkable. I’ll just share from two textbooks.
Adams, D. (1848). Arithmetic: in which the principles of operating by numbers are analytically explained and synthetically applied : illustrated by copious examples : designed for the use of schools and academies (Rev. ed.). Keene, N.H.: J.H. Spalter & Co..
Exertion, then, to bring teachers to a higher standard, will be more effective in improving school education, than any efforts at improving school books can possibly be. It is here where the great improvement in must be sought. Without the cooperation of competent teachers, the greatest excellences in any book will remain unnoticed, and unimproved. Pupils will frequently complain that they have never found one that could explain some particular thing, of which a full explanation is given in the book which they have ever used, and their attention only needed to have been called to the explanation.
Colburn, D. P. (1862). Arithmetic and its applications: designed as a text book for common schools, high schools, and academies. Phililadelphia: H. Cowperthwait & Co..
In the first place, such tests are unpractical, for they can never be resorted to in the problems of real life. What merchant ever thinks of looking in a text book or a key, or of relying on his neighbor, …?
When a pupil, having left the school room, performs a problem of real life, how anxious is he to know whether his result is correct! Neither text book nor key can aid him now, and he is forced to rely on himself and his own investigations to determine the truth or the falsity of his work. If he must always do this in real life, and if his school course is to be a preparation for the duties of real life, ought he not to do it as a learner in school? Is it right to lead him to rely on such false tests?
Besides, the labor of proving an operation is usually as valuable arithmetical work as was the labor of performing it, and it will oftentimes make a process or solution appear perfectly simple and clear, when it would otherwise have seemed obscure and complicated.
But some of the exercise problems are just insane. I intentionally looked only for exercises in division of whole numbers. And all these textbooks were for school-aged children, grades 4 through 8.
1909, Walton & Holmes:
408903 ÷ 3508
147500 ÷ 6190
1921, Thorndike:
748275 ÷ 825
42974 ÷ 8523
1862, Colburn:
55673 ÷ 6349
2700684 ÷ 19743
1848, Adams:
46720367 ÷ 4200000
reduce to lowest terms: 468/1184
1843, Bonnycastle:
4637064283 ÷ 57606
Common Core looks better than this.
MathEd Out Podcast
Adrian Pumphrey was very kind and patient when he interviewed me for this month’s MathEd Out podcast.
Other folks whom Adrian had interviewed thus far:
Julie Reulbach — blogs at I Speak Math
Dan Meyer — blogs at dy/dan
Lynne McClure — Director of NRich
Daniel Schneider — blogs at Mathy McMatherson
Sue VanHattum — blogs at Math Mama Writes
Upcoming interviews:
Bill McCallum — Lead author of CCSS
James Grime — Numberphile
Malcolm Swan — MARS
Thank you, Adrian, for the honor and pleasure to do this. I’m really bummed that I won’t be at #TMC14 to meet you in person.