My Other Math Sites
Lessons From the Classroom
That Sinking Feeling
Whoever installed this bathroom sink unit did not use it to wash hands, nor did they use it to rinse out a washcloth. It’s very shallow and the spout is toward the back of the basin. The water inevitably spills onto the back counter, and the washcloth half dangles in the dirty water that hasn’t drained from the shallow sink.
And this entire awful design flaw is not worth talking about until I realize it’s installed in every guest room at this 450-room-plus hotel. How did this happen? How could a mistake like this happen on such a grand scale? How many people used this sink and thought it was functional [which it isn’t], but rather they didn’t speak up, “Whatever, I’m just installing, won’t be staying at this hotel anyway.”
I think of the materials wasted. The time it took to install. The cost. The unnecessary wiping around the sink each time. How the user — of this thing that it was designed for — was ignored.
But the parts are actually fine, right? Good widespread faucet, solid granite countertop, okay-for-washing-small-hands-only sink. Someone just screwed up on the assembly. There should be a guideline that a faucet must be installed so the water flows out at a minimum of three inches from the back edge of the sink.
This whole thing makes me think about a bad curriculum that ends up on students’ desks. How did this happen? How could a mistake like this happen on such a grand scale?
A First Grade Lesson Using Vertical Whiteboards
As we wrapped up our book study of Peter Liljedahl’s Building Thinking Classrooms, and in my role as TOSA (teacher on special assignment) I do not have a classroom of my own, I asked one of our first-grade teachers if I may facilitate a thinking task using vertical whiteboards with her students.
To supplement the teachers’ classrooms with more whiteboard space, I reached out to Wipebook for durable dry-erase chart paper surfaces (with grids on one side!). The reusable Flipcharts they sent were the perfect tool to use over her glass doors and windows! They can easily be removed and reused as many times as you want — an eco-friendly solution to reduce paper waste. Our district has also purchased whiteboard easels with adjustable heights.
The teacher already had her groups paired up with their “thinking partners.” Each whiteboard space was labeled such as “Blue 1 and 2” so the students knew where they would be working.
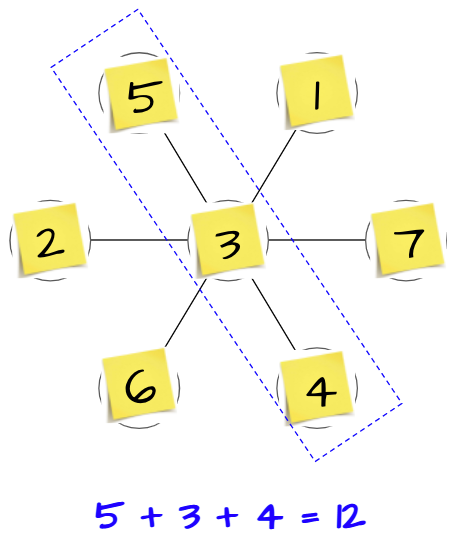
We had the students sitting on the carpet area for me to launch the task. I taped this flower image on the board and asked how many circles they saw. They said seven.
Then, I counted out along with them seven sticky notes, marked from 1 to 7. This great Flower Petal Puzzles thinking task is from Dan Finkel, founder of Math for Love. The intent of the task was for students to write the numbers inside the circles/petals and to keep track of numbers they have used by crossing them off at the bottom of the page. Dan also suggested using counters. However, I wanted the students to do these vertically, so counters would not work, and writing numbers in and erasing them is challenging and cumbersome, especially for young students. The use of sticky notes was really key in helping students stay focused on the task because it was easy to swap out numbers and keep their brains moving.
I called up one student at a time to place a numbered sticky note into an empty petal without further instruction or stating what the goal was. When there was only one space left, I said it was my turn and placed the number in. I wish I had taken a picture of the board at this point. But since I didn’t, below is a picture of the flower with randomly placed numbers. I then told them these three petals are connected and asked them for the sum and wrote the equation.
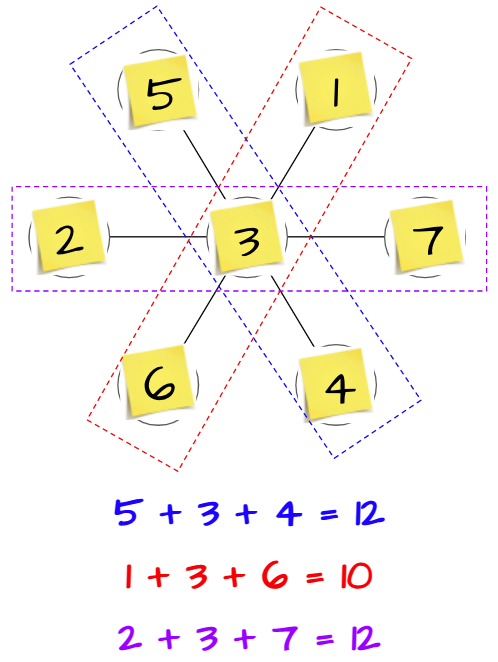
We found the sum of the other two groups.
It was not until then that I told them the challenge of the task was to have all three sums be the same. And that the sum is 10. So off they went with their thinking partners to their whiteboards!
Sure enough one pair got the solution within 5 minutes, and we asked them to keep their equations (not erase them), and to do the next challenge which was to get a sum of 12 for all three equations. Some time later, all of the groups except for two got the 10 puzzle. We came over and applauded them for their perseverance and asked if they would like a clue. They nodded and we let them know to place the number 1 at the center of the flower. When this group got the solution with the hint, the girl excitedly said to me, “This is a lot of fun!”
I tweeted this out later as truly it was the best hour with first graders for me. So much perseverance, so much thinking, so much fun. The groups were in different stages (finding sums of 10, 12, and 14), and two groups ended the hour working on the “ultimate challenge” of creating their own puzzle using a 9-petaled flower.
Updated 04/11/2022
I just thought of a way to take this 1st grade task to next level. https://t.co/7vQzKk4kuP
— Fawn Nguyen (@fawnpnguyen) April 1, 2022
7 circles: possible sums r 10, 12, 14 (what #s go in middle circle of these sums, respectively?)
What r possible sums for n (odd) circles? How many equations [of equal sum] for each n?
A Routine for Between 2 Numbers
I hadn’t realized the last few entries of between2numbers.com were left blank. They are done now. Thought I’d share a more revised warmup routine of how I’ve used the contents.
I’ll use entry #1 as an example.
I project the two images only and set the timer for 30 seconds for quiet notice-and-wonder. No writing necessary during this time.
I then say, “Before I show you the speed of each of these, I’d like you to discuss with a neighbor what the numbers might be, let’s think miles per hour.” I ask them to write down their estimates [in a journal]. Set the timer for another minute.
I call randomly on two students to tell the class what their guesses are for the snail. Call on two more students for their guesses for the jet. I record these on the board.
Now I reveal the snail’s rate and ask, “Who has the closest guess to this?” Record their answers. This is a good opportunity for students to check their decimal comparison.
Now I reveal the jet’s rate and ask for the same.
I entertain any other related information at this point. I might ask them if they knew what the average speed of a passenger airplane was. Then, I reveal the question.
Okay, this step is important. It saves time writing and fussing over actual quantities, and I find that it helps students focus on the mathematical operation rather than feel anxious about the numbers. I say, “We’re going to let the snail’s rate be A, the jet’s rate be B, and the distance 2,800 miles be C…”
“... Discuss with your neighbor what calculation(s) you would do to find out how much time it takes each object to travel across the US. Just use the letters now. For example, if you wanted to add the two rates, you’d just write A + B.” Set the timer for one minute.
Randomly call on one group to share. Record on the board what they share and ask, “Who has a different solution?” Write down what they say. Continue asking until I have recorded all the different solutions. (Normally, there are usually just 2 or 3 different ones.)
I now take out a calculator and get an answer for each of the solutions shared. I go back to the owners of each solution and ask, “What unit should your answer have?” (If the units were not mentioned earlier.) We discuss the reasonableness of the correct answer.
I’m proud of this site because the routine affords several of these:
interesting facts
estimating
talking and listening
proportional reasoning
unit rates
dimensional analysis
Here is the key. Please share this resource widely, and if you use it, please let me know how it goes.
Number Talks for Middle Schoolers
If I may recommend only one thing to K-12 classrooms, that thing has to be number talks. As a warm-up routine, it usually takes less than 10 minutes, yet it pays dividends in building number sense, connecting computational strategies, honoring flexible thinking.
I finally finished this set of 90 number talks for middle schoolers — enough for a full school year if you do this routine every other day. But I hope you’ll also share it with your elementary and high school teachers to inspire them to create their own or modify these.
I’ve already shared my notes about the routine on the first 4 slides. I just want to add that each slide — or each group of 3 slides — is intentional, meaning there are several strategies that I hope your students and you will explore and share. My goal is also to tweet these out, one at a time, and include people’s responses on a slide following it.
You know what you should do on the other 90 days. :)
Comparing Fractions
I was taught to find a common denominator when comparing or ordering fractions. Find the LCM. Even change them into decimals.
Instead, I want to compare fractions in these three ways:
Using number sense and the fraction 1/2
Finding a common numerator
Thinking of them as perfect pinks or not
Compare 3/4 and 5/12.
3/4 is more than 1/2, and 5/12 is less than 1/2, hence 3/4 > 5/12.
Compare 1/5 and 2/7.
1/5 is the same as 2/10, and 2/10 is smaller than 2/7 because pizza.
Compare 5/7 and 6/9.
A perfect pink color is made from 1 part red and 2 parts white, expressed as 1/2. I have a visual sense of this color, this red/white ratio of 1/2. Anything greater than 1/2 is dark pink, and anything less is light pink.
So 5/7 is darker, and to get to the color of 6/9, I’d need to do this: 5/7 + 1/2 = 6/9. If I’m adding something less dark than what I’d started with, then I’m going to dilute the color, so 6/9 is less dark than 5/7. I conclude 5/7 > 6/9.
Of course if I add the exact same color to itself, then there should be no change: 2/3 + 2/3 = 4/6.
Compare 19/60 and 21/55.
19/60 is light pink, so is 21/55. To get from 19 to 21, I’d need to add 2 reds, and to get from 60 to 55, I’d take away 5 whites. The net effect is more red, making 21/55 darker, or 19/60 < 21/55.
This is not unlike how batting averages work.