My Other Math Sites
Lessons From the Classroom
Reviewing for a Test
There's not enough time or humility for me to share my teaching fails, but here's a test review routine that worked well with my students.
I pass out the review questions near the end of class and say:
Chapter 3 Test is scheduled for _____. To review for it, I need you to look through the ten problems on this paper. You're more than welcome to work on the questions, but you don't have to, not for me anyway. I need you to just examine them enough to identify two questions that you feel confident about, that you have no problem solving. Then, I need you to identify two questions that you would like to get help on most. That's it.
If you have human students as I do, they will ask questions and you'll have your answers ready.
What if I'm confident I can do more than just two?
Possible Answer (PA): That's fantastic! But, nobody cares. I just need you to tell me two.
What if I need help with more than two questions?
PA: That's why I said most... two questions that you would like to get help on most.
What if I can do the whole test? I mean I don't need help with anything.
PA: Then don't mark anything down when I ask tomorrow. Or, if you just have one question that you need help with, then identify just that one. Also, you'll get to make the test key for us.
What if I'm not confident with any of the questions?
PA: Thank you for that question! I hope you'll find time this evening to see if you can attempt two of them. Then, please send me an email letting me know if you were successful. Remember, the answers are on the back of the review questions.
You said we don't have to actually do the problems. But can we do them for extra credit?
PA: No.
How many questions will there be on the test?
PA: Ten. Or maybe thirty-five. I don't know. It'll depend on what you tell me about these review questions.
The next day, the whiteboard already has two columns drawn, and students know to give two tally marks in each.
If I were to do this again, I'd also send my students home with these two questions in Desmos instead. When you ask for a checklist in Desmos, you get an auto tally of how many students marked that choice in the teacher dashboard.I focus on the right column and say:
I want to make sure we go through all the questions on the right column. We'll start with question 4. There are at least four of you here who marked that you are confident with this question, I need one of you to please show us how to do question 4.
And we continue down the list. Notice that I ask students to work on the problems. They learn better from their peers, especially during review time. I get to check for understanding as there are occasions when the "confident" student has done the problem incorrectly. We spend class time on more targeted problems, including admitting which concept needs a serious revisit. I have them do this — looking over the questions — at home rather than in class because I need them to focus, without peer pressure and distractions. I want them to feel free to look back in their notes, in their textbook, search online, ask for help. I want honest feedback.
After we've gone over all the questions on the right column, that evening I create the test with four questions already done by choosing two from the left column that had the most tally marks, in this example, questions 1 and 2, verbatim. It's my selfish way of not having to see a test with a score of 0 which leads me to self-loathing. Then, I pick two questions from the right column that we'd gone over, also verbatim. I can actually hear the sighs of relief when students see the same questions from the review sheet.
This routine works well for regular homework too. Assign the homework without actually have them do the homework: ask for two "easy" questions and two "tough" questions. Let's not have them work on problems that they already know how to do, instead, let's spend time together in class to work on the ones they need help with. Promise me you'll only step in to show how to do the problem when no other student in the class is able to. :) But even then, I'd say, "How about someone starts out this problem, help us with that, just take it as far as you can, and then I'll take over from there."
Changing Up Popular Warm-Up Routines
As with any task, whether it's a warm-up or a curricular task, I try to think of ways to get more student engagement, tap a different thinking modality, and just to change things up.
WODB has become a common acronym in classrooms for good reasons. (Actually, does it qualify as an acronym like NATO since I've never heard it pronounced as a word? Y'all are still saying Which One Doesn't Belong, right?) Take this first one I see on the site. (I added the numbers 1-4.)
I do my homework first, in the order that the shapes come to my brain:
#2 doesn't belong because it's the only non-triangle.
#4 doesn't belong because it's the only shaded shape.
#1 doesn't belong because it's the only one with exactly one line of symmetry.
#3 doesn't belong because it's the only obtuse triangle.
With students, I ask them to give me a blank grid and get ready to draw in each box as they listen to my clues. I tell them to make quick sketches as they may need to make changes when they hear new clues. I can give them the clues in any order I choose. But, we'll stick with the order above.
#2 doesn't belong because it's the only non-triangle
A possible sketch:
#4 doesn't belong because it's the only shaded shape.
#1 doesn't belong because it's the only one with exactly one line of symmetry.
#3 doesn't belong because it's the only obtuse triangle.
Students can then share their sketches and critique each other's work. The reveal is fantastically fun.
Estimation 180 is another popular one. From the site's Day 6:
Instead of asking students for an estimation, I ask:
One of the four numbers below is the correct number of almonds in the 1/4 cup pictured. Which one is it and why did you choose it? Which number do you believe is way off?
8
15
28
40
I find their reasoning and conversations are tighter this way — more focused. I'm also one of those people who dread having to guess at something, even with a visual clue. With younger students, I'd give them 3 choices instead of 4.
Open Middle is another well-loved routine. This one is filed under Grade 4, Equivalent Fractions. (I added the digits A-G.)
Directions: Use the digits 1 to 9, at most one time each, to make three equivalent fractions.
I mark the digits 1 through 9 on red/yellow counters and put them into a baggie. I reach into the bag and randomly pull one out. Say, I pull out a 5. I call on a student [randomly] and ask, "Which space (A-G) can the number 5 not be in?"
There is a big difference between asking the above question versus, "Where do you think the number 5 goes?" The chance of answering this question correctly, if 5 is used at all, is 1 out of 7. The former question is much safer to tackle. This routine engages the whole class on one number at a time — we get deeper thinking when we can focus on one thing and while building on each other's thinking. And I very much love it when students are given opportunities to honor and build on their classmates' reasoning. After a few suggestions, a student might conclude that the number 5 can go into the discard pile. (It's also common for students to use a number more than once or use a number not allowed, so the counters alleviate this mistake.)
Also, I need to share that this problem was posed in an online workshop I attended yesterday, and I didn't even attempt it because these are my constant truths:
Someone else will come up with the answer before I do.
The answer will be revealed before I get to solve it, so no point in me ever working on it.
How many of our students also hold these truths? I understand this was a workshop for teachers and time is limited and sharing is good and all that. I'm just thinking about best practices with students though.
[Added 10/17/2020]
I meant to include a numerical WODB example because there are a lot of possible solutions, it's always fun to see what the kids come up with. Here's the first numerical one on the site. (I added the letters A-D.)
I work on it first.
D is the only non-square number.
A is the only single-digit number.
C is the only number divisible by 5.
B is the only even number.
I give the students the above clues in the same order. However, students may not erase a number as they revise, they may only cross it off so that I may see what they had originally.
MoMath
That sign is for ALL of us!!... Fucker!
I heard the angry man yell around 8:00 this morning. Our house sits at the corner of 4-way stops. Glad he was out there to give the driver a piece of our collective neighborhood mind. At our core, we sense when something is not equitable, not right. We want to speak up when someone is not abiding by the guidelines that are meant for all of us.
I saw the tweet below from Sam Shah yesterday, which I retweeted without comment after reading his post.
Howdy all, I wanted to share some concerning things I've been made aware of at the Museum of Mathematics (MoMATH). I hope the Board of Directors looks into things. https://t.co/ftLlFCBuXr#MTBoS
— samjshah2 (@samjshah2) October 11, 2020
Nothing I could add to the tweet to make it less upsetting. I had always wanted to visit MoMath when I could make it back to New York City.
Something is not equitable, not right. I spent most of my teaching at Title 1 schools: 11 years at George Middle School in Portland, Oregon, and 17 years at Mesa Union Junior High here in the same county where I live.
Good bad and indifferent, these children are mine. When I read that MoMath treated students from Title 1 schools less favorably and dismissed the voices of those who brought this fact to light, I'm made to distrust those in power, those who can do so much more to improve our children's livelihoods, instead they further marginalize them.
@MoMath1 is responsible for making itself worthy of all our students' learning and enjoyment of mathematics. That museum is for all of us.
One-Word Writing Prompts
Years ago at George Middle School (Portland, Oregon), the teachers were allowed to teach something we were passionate about. The class would be twice a week, right after lunch, for just 20 minutes. I was a science teacher at the school and asked if I may teach "writing for writing." My principal reacted with slightly more enthusiasm than my [male] colleague's "The Simpsons." I had a simple plan:
Given a prompt, we write for 5 minutes. It's imperative that I write along with my students.
We share aloud what we'd written, only if we choose to.
We also share what we'd like to do next with our 5-minute piece:
scrap it
add it to an existing piece of writing
save it for whatever whenever
get feedback on it
Typically, writing prompts come in the form of questions. Here are the first three of "34 Quick Writing Prompts for Middle School Students" from Journal Buddies:
What does the city sound like at night?
What is the coolest thing that can be found in nature?
How can you tell whether or not someone will be a good friend?
These are fine, of course. But personally, I either don't have a lot to say about the prompt or I don't care. And it's hard to think of a question that everyone cares about or have copious thoughts on. Let me try the above prompts right now, as if I were a middle schooler.
What does the city sound like at night?
The city is quiet at night. Though I'm not sure why I'm in the city at night when I should really be in bed at home. I'm a kid. Sure, there are times when I can't fall asleep or I wake up in the middle of the night. But it's still pretty quiet at night. Sometimes I can hear my Dad snore. (Or is that my Mom?) If only it would rain each night because that's the best sound to fall asleep to. But then I think about the homeless people. It sucks to be homeless, so for them, night rain is probably the worst...
What is the coolest thing that can be found in nature?
The coolest thing that can be found in nature is... I don't really know. I'm not sure if it's the "coolest" thing or even just "cool," but I like flowers and plants. I pay attention to them whenever I go on walks. My favorite house is always the one with lots of flowers, especially when they are overflowing in window boxes. They don't require a lot to grow, not like what my two cats and dog require. I like flowers that smell good.
How can you tell whether or not someone will be a good friend?
I can tell that someone will be a good friend because they are not bad. But I've been wrong lots of times before. They start out all nice and friendly, they say the right words and do the right things, then they just turn. Sometimes they turn so quickly that I have no clue what happened. It's like they have an R gear for reverse and they just shifted into that gear and ran you over. I guess there are no guarantees whether or not a person will be a good friend. Look at all the divorces and breakups! It's best to just take one day at a time.
I’m weary that a question prompt might not elicit interest or intrigue, and then I have to hear them whine pitch perfect, "But I don't know anything about that," so I give only one-word prompts.
tiny
red
outside
wax
intelligence
breakfast
sand
scream
pale
rain
My goal was writing for writing. I wanted the pen or pencil to move across the page for five minutes. I wanted the shitty first drafts. Any more than that one-word prompt might inadvertently restrict, if not constrict, their thoughts. I wanted them to feel free to write freely about the color "ecru," the noun "home," the verb "shrink," the adjective, "dull." They wrote wildly, ferociously, thoughtfully. So did I. Mainly, I didn't want any student of mine to feel the way this perennial prompt made me feel through all the school years, "What did you do last summer?" Eventually, I got tired of lying about the trips that my family couldn't afford to take and left my paper blank.
Common Denominator
I already wrote about dividing fractions here and here.
I use the explanation of "dividing by one" to explain why 5/6 divided by 2/3 is the same as 5/6 times 3/2.
But when I was asked recently about how the "common denominator" strategy worked, my muted response was, "Because it does." I didn't mean to be a jerk, rather I just hoped she'd go along with me.
I grabbed a piece of paper and wrote 5 ÷ 3 = 5/3. She was already bored with me. Then I added 1s under the numbers to show 5/1 ÷ 3/1 = 5/3. Right, right? I then changed the problem to 10/2 ÷ 6/2 = 10/6... = 5/3. Still okay, right?
Before I could give another example, she took the paper and rubbed it on my head. Rude.
***
The real common denominator is we're all in this together to #flattenthecurve. This tweet is like rainbow.
My elderly neighbor is self-isolating. So the neighbor kids are playing her a cello concert from her patio. pic.twitter.com/g6Nr2HNVho
— Jackie Borchardt (@JMBorchardt) March 16, 2020
Math Worksheets
I often create worksheets for my students, even though every district-adopted math curriculum we've had has worksheets for students. I do this for two reasons:
I sometimes want to teach differently than what the curriculum writing team was thinking.
There's a particular structure/scaffold that reflects how I see the content can unfold for learners.
Here's a sequence of practice questions for my 8th graders on rigid transformations.
Everything about this is intentional.
Item #1 is a completed sample of what's to come. This is a practice worksheet, not a problem-solving task, so I will be clear about what is expected.
I remove certain parts in item #2, while keeping it similar to item #1.
Item #3 comes before item #4 because I think it's easier to follow the stated transformations than to say what they are.
Item #6 asks for more flexibility but with an ending constraint.
Item #7 opens up the problem and allows for peer exchange.
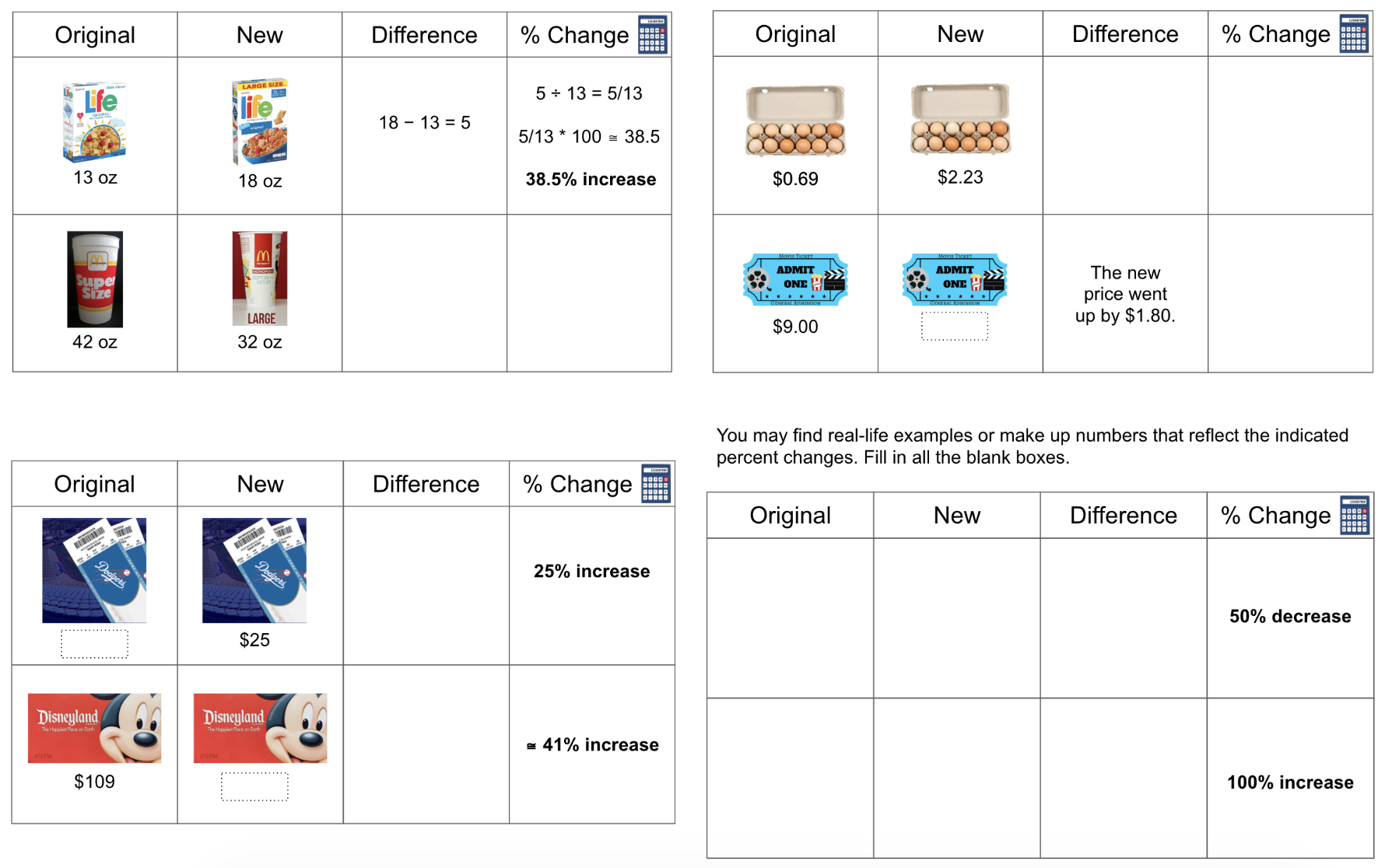
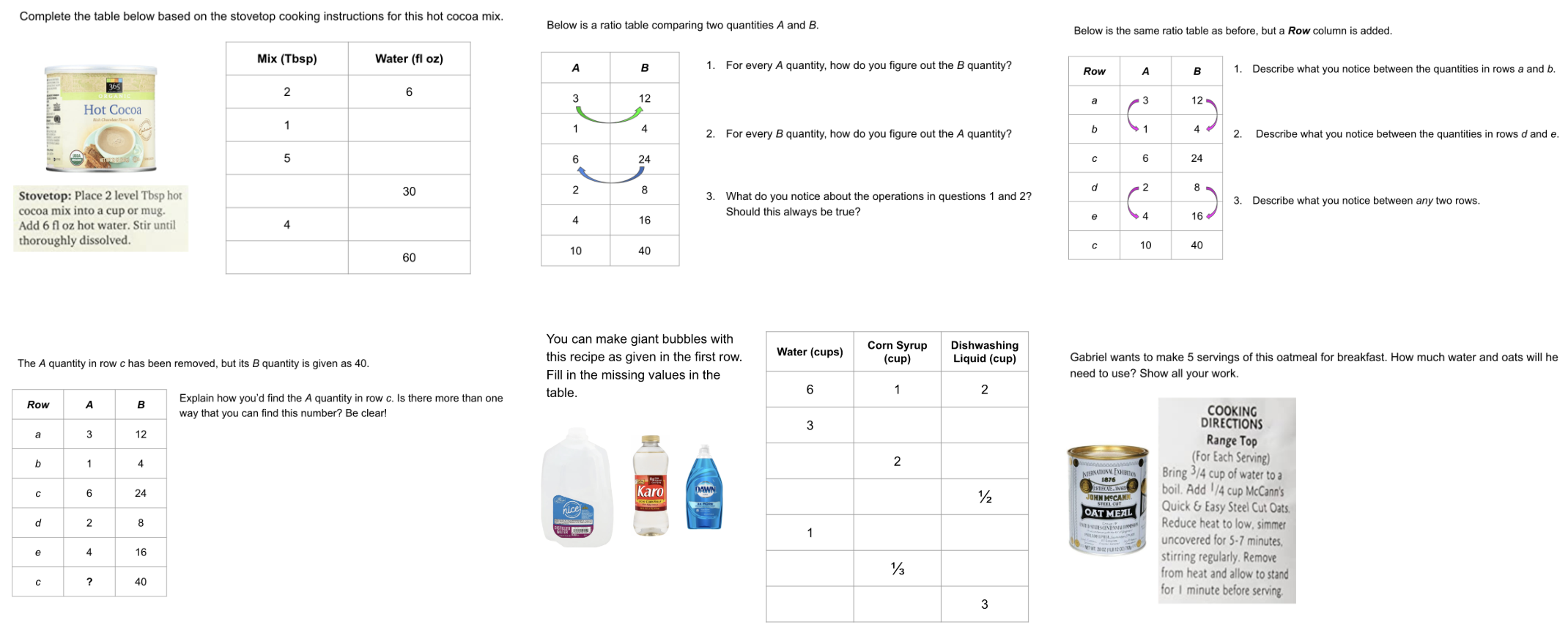
It's esthetically easier for me to create the questions on Google Slides. I then do screenshots to toss them onto a Google Doc. Here's a screenshot of questions for 7th graders on percent change. Here's a screenshot of questions for 6th graders on ratios and rates. If you'd like copies of these:
Yes, each of these takes one unit of shit-ton of time, especially when I have to look up real products with real numbers. But it's an OCD thing too, as in If-I-can-make-it-better-I-will. Stay safe, everyone.