Giving Feedback With a Highlighter

I attended John Scammell's excellent 3-morning sessions on Formative Assessment at #TMC15. We were asked to share strategies that we may already be doing to give students feedback . I shared about how I used highlighters for this. I promised my group that I would write a short post about it, but I waited until now since I needed the school year to begin to have student samples to share.

I used highlighting to give my 6th graders feedback on their first PoW (Problem of the Week from The Math Forum).

It's challenging, as I hope all PoWs are, and even more so when it's the first one they get. I give no specific instructions on how they should write up their solution — nothing more than the usual "show all your work in order to receive credit." I want to see what raw stuff I get on this first submission. We'll worry about quality control soon enough.

I'm familiar with what I can expect with the first harvest of solution write-ups. One-fourth of the papers are pleasantly stellar, one-third show candid efforts (especially the ones with parents' writings on them), another third make me get up and stick my head in the fridge to find a cold-and-alcoholic beverage, and the rest of the papers remind me that some of my 6th graders are still working on finessing the opening of their combination locks.

Years ago I taught a writing elective. I was at the beach — at the Oregon coast — because that's where you should read and grade all writing papers. I forgot my red pen. I only had a yellow highlighter. The highlighter transformed my grading. I no longer cared so much about the writing mechanics — fuck spelling and punctuation and syntax. You got voice in your writing, kid. Your heart was wide open in this third paragraph. How did you know the rain smelled differently depending on what part of Portland you were in?

I highlighted sentences and words that spoke to me. I highlighted a brave sentence. I highlighted the weak ones also. The highlighter allowed me to interact with the kids' writings differently. I didn't add to or cross out anything they'd written. The highlighter didn't judge the same way my red pen was judging.

And that's the history of using the highlighter for me. But back to math. I have over 100 students and to write feedback for their bi-weekly PoW write-ups is all too time consuming. The different colored highlighters come to my rescue.

I'm going to continue using my binary scoring system because it worked well last year. I look through all the papers, separating them into two piles: papers that got it (full 10 points) and papers that fell short (1 point). These kids will get another week to revise their work and re-submit.

I use my yellow highlighter — just swipe it somewhere on their paper — to show that I'm having trouble understanding their work or that their work is lacking.

I use the pink highlighter to show that the answer is not clear, not specified, is partially or entirely missing.

I use another color (like green or blue) if the papers warrant another something-something that I need to address. I didn't need to with this week's PoW submissions.

If necessary, I will write on their papers directly. But I don't have to do too many of these because kids' mistakes, more often than not, are similar to one another.

When I pass the papers back, I tell students what each colored highlight means and what they need to do to revise their work, including coming in to get help from me. It's a helluvalot faster than what I used to do.

A Book: Thinking Mathematically

I'm re-reading Thinking Mathematically, an assigned book from a math course I took years ago in Portland. I was teaching science at the time but signed up anyway because I've always loved math.

Thinking is still so good and resonates much more now that I've been teaching mathematics.

In the Introduction, under "How to use this book effectively!":

Recalcitrant questions which resist resolution should not be permitted to produce disappointment. A great deal more can be learned from an unsuccessful attempt than from a question which is quickly resolved, provided you think about it earnestly, make use of techniques suggested in the book, and reflect on what you have done. Answers are irrelevant to the main purpose of this book. The important thing is to experience the process being discussed.

... our approach rests on five important assumptions:

You can think mathematically Mathematical thinking can be improved by practice and reflection Mathematical thinking is provoked by contradiction, tension and surprise Mathematical thinking is supported by an atmosphere of questioning, challenging and reflecting Mathematical thinking helps in understanding yourself and the world

These assumptions need to live in our classrooms.

The problems in Thinking are mostly brief and simply stated -- yet each one has the potential to make you linger a bit longer because you want to savor your own thinking. Not even productive struggle, this is sweet struggle.

How many rectangles are there on a chessboard? [Page 43]I have just run out of envelopes. How should I make myself one? [Page 35]A certain village in Jacobean times had all the valuables locked in a chest in the church. The chest had a number of locks on it, each with its own individual and distinct key. The aim of the village was to ensure that any three people in the village would amongst them have enough keys to open the chest, but no two people would be able to. How many locks are required, and how many keys? [Page 176]

I'm finding out that the 2nd Edition came out in 2010. Amazon does not have it in stock currently, but when it does become available, we can rent it for $54.77 or buy it new for $91.29. What??

Desmos Puppy House

We don't cover quadratic in Math 8 this year, so we really can't do Des-man. I come up with "Puppy House" instead so my students can still create something that allows them lots of practice with writing linear equations with domain and range restrictions.

They draft the house on paper. The house needs to have a minimum of 6 slanted lines, 5 vertical lines, 5 horizontal lines, and one image of a puppy at entrance of house.

Below are the ones from my Math 8 Honors kids who learned quadratic last year. They completed these within one 55-minute period. So proud of Ashlynn for remembering how to write inequalities.

Riley

Andrew

Ashlynn

I'd love to see what amazing dog houses your students will create. (Someone create a flap door for me to play peek-a-boo with the puppy please!)

Students Practice Scoring Short-Text SBAC Responses

A few weeks ago I attended an all-staff PD at the County Office. During the morning session we scored samples of 2-point short-text items from grades 4, 8, and high school. It was time well spent. I wanted to duplicate that experience for my students with two goals in mind:

1. See how well they can interpret and use a scoring rubric.

2. For them to attend to the same thoroughness and precision in their own solution writing when it's their turn in May.

What I had my students do:

1.  Get to know the short-text item.

They worked on the grade 4 item below. This was intentional to diminish any math anxiety and to keep our focus on the scoring of the task.

While it was good to learn of my kids' different solutions, it was also disheartening (but not too surprising as they are the same ones who struggle mightily) to learn that 20% of my 6th graders did not get the correct solution for this grade 4 item.

2.  Go over the solution.

I collected their papers and just had a couple of kids share their strategies to the whole class. Considering 1 out of 5 kids in the room didn't quite know how to solve the problem, this step was really for them.

3.  Get to know the item-specific rubric.

I gave the kids quiet time to read the rubric, reminding them that they would use this rubric to score 9 students' solution responses. I told them that they could expect to return to the rubric over and over again as they scored each response.

4.  Score the responses.

I gave them quiet time to fill out Score 1 column of this handout. I reminded them that this was one of the main goals of the task -- to score the sample responses fairly and accurately using the item-specific rubric.

Why are you giving this response a 1? What is it missing to not get a 2? What does it have to earn a 1 and not a 0? Keep referring to the rubric! Does spelling matter? What does your rubric say about spelling errors?

After everyone was done filling in Score 1 column, I asked them to talk to their neighbor/s and only fill in Score 2 column if they changed their mind. (They were not to erase any score in Score 1 column.) This also made it easy for me to see how many scores they'd changed their mind on.

My favorite thing in the whole wide world is to listen in on their conversations about math.

5.  Reveal the actual scores.

[The actual scores are on 2nd page of handout above.]

If the whole class agreed with the actual score for a particular student response, then we moved on. But if anyone disagreed, then I had that student tell the class why. Then I had another student who agreed with the answer to share his/her reason.

Out of 66 students, 24 students scored 9 of 9 correctly, 19 students scored 8 of 9 correctly, and 6 students scored 7 of 9 correctly.

That meant 65% of my 6th graders did this scoring-using-a-rubric better than I did. Whatever.

I also asked the kids to write a couple of sentences about what they got out of doing this. Most of their responses echoed these:

This was helpful to me because now I know I need to be much more thorough with my work and explain why I might of did something.

This was helpful to do because it let us see how these problems are graded.

Even though the problem was for 4th grade, I think the grading scale of conclusion and math will be similar or the same for all problems like this.

I believe this was helpful because when I take the test, I will be more aware of the questions and what is expected of me. I will make sure to always back up my answers with evidence.

Grade 6 Rocks Visual Patterns

I'm always happy to hear how teachers use visualpatterns.org with their students.

Michael Fenton shares how he uses the patterns with Desmos. And this.

Alex Overwijk's students use the big whiteboards.

Whiteboard photos of http://t.co/ajYFLzRQSU that my S's did yesterday....thanks @fawnpnguyen #mtbos #mathchat pic.twitter.com/UZd3HPfyoL

— Alex Overwijk (@AlexOverwijk) March 7, 2015

Bridget Dunbar removes some figures, and kids need to draw them in.

Visual Patterns and Missing Figures https://t.co/QDvPNlKRSZ Thank you @fawnpnguyen

— Bridget Dunbar (@BridgetDunbar) March 5, 2015

Kristin uses the patterns with 5th graders.

Snowflake Visual Pattern work in honor of our non-snow day! cc @JustinAion @fawnpnguyen #visualpatterns #mtbos pic.twitter.com/n6SZuigK5X

— Kristin Gray (@MathMinds) January 28, 2015

I do patterns with my students on Mondays as part of our warm-up routine. I've already shared 28 pattern talks (and 28 number talks) on mathtalks.net, but I'd like to share a couple more here because my 6th graders have made incredible gains in seeing a pattern in different ways and in articulating an equation to go with each visual.

This is pattern #153. I'm sharing this one because I meant to only use it with my 8th graders, but my printer was acting up and failed to print a different one for my 6th graders, so I just used the same one. Fun challenge!

Student 1:

I see these 5 spokes coming out. Each one has n number of hexagons. In between these 5 are Gauss. So, the equation is... five times n, plus five Gausses.

 Hexagons = 5n + 5(1+n)(n/2)

Over time, my students have come to recognize Gauss addition very quickly. They have used Gauss as a verb and a noun, as in, I Gaussed it or I saw two Gausses in the pattern.

Student 2

Each step adds another ring of hexagons on the outside. Looking at the outer most ring, I see three groups of (n+2), plus a leftover. The leftovers are odd numbers. So, the outer ring alone is 3(n+2) + 2n-1.

And the rings add like Gauss!

Together we write the equation carefully, talking through each step.

Gauss means adding the first and last steps together, then multiply by the pairs of steps. The last step is the outer ring, the first step is the inner ring, which is always 10. So, 10 plus the outer ring, then multiply this by the number of pairs [of rings], which n/2.

Hexagons = [10+3(n+2) + 2n-1](n/2)

We were confident we had the correct answer when both equations simplified to the same equation.

Hexagons = [(5n^2)+15n]/2

This is pattern #147. I'm sharing this one because of the many different ways kids tried to see the pattern. Normally, when I randomly call on a kid to share and someone had already shared their same way of seeing, then they just have to come up with a different way.

Ducks = (n^2) + (2n+1) + n

Ducks = (n+1) + (3+2n+1)(n/2)

Ducks = n(n+2) + (n+1)

Ducks = 2(1+n)(n/2) + (n+1) + n

Ducks = (n+1)(n+2) - 1

Ducks = (n+1)^2 + n

I very intentionally do not have kids fill in a table of values for visual patterns. I'm afraid it becomes a starting point for them every time instead of just looking at the pattern itself. For our 8th graders using the CPM curriculum, which I like a lot, there are plenty of opportunities in the textbook to tie all the different representations (table, graph, rule, sketch). These are my 6th graders who are writing quadratic equations without all the fuss right now.

Please continue to share the site. What I love most is learning that the patterns also get used in elementary and high school classrooms.

Reversing the Question

Don Steward posted this on Sunday. Like Don, I really like this task and also think it has a certain Malcolm Swan je ne sais quoi about it.

I showed only the top part to my 6th graders, and I gave them 2 minutes to write down what they noticed.

In addition to noticing the given information, the students also mentioned:

It takes a lot of grams to make a sponge cake.

A kilogram must have a lot of grams in it.

The unit of measurement is changed in the cake and in the big bag.

This problem doesn't have a question.

The sponge cake has no price.

There is frosting on the cake.

You need to change the measurements first (kg - g)

The cake weighs more.

The cake is really small and the flour is really big.

Not much information and there's no question.

There is no question.

The weight of the bag is in kg but the flour it takes for the cake is in g.

You have to convert 24 kg to grams.

It uses only very little of the flour.

I gave them another 2 minutes to write down what they wondered.

How much the sponge cake costs.

How many sponge cakes can you make.

How big is the sponge cake.

How to convert from kg to g.

If the sponge cake is good.

24 kg is <, =, or > 150 g.

What we are going to have to solve.

Is the question going to be about if there's enough flour or is it going to make us change it from kg to g.

How much 24 kilograms is in pounds.

How many grams are in a kilogram?

How many krumkakes can you make with the bag of flour.

How long will it take for the cake to be ready.

What a sponge cake is and what the recipe is for the cake.

How much flour is left.

What flavor is the cake. (Sorry. I'm hungry!)

What you're wondering that I'm wondering about.

What the question is, and if there are more ingredients.

If we will have to find the price for the sponge cake, or maybe we have to find out how much half as much flour is worth.

Then we moved on to next part of providing questions that would go with the calculations. This was so very tough for my kids. While 21 of 31 kids could come up with the correct question for part (a), they were lost with what to write for the other three parts.

Because we didn't care what the numerical answers were, the kids didn't do any calculations, instead they were supposed to focus on the operation(s) in each problem and decide on the question that would prompt a specific operation.

The most common question for part (b) was, "How much does 1 kg of flour cost?" (I'd swapped out £ for $.)

Then my next step would be for them to go ahead and use a calculator to get the numerical answers. They will see that for part (b), 24 divided by 21.50 equals approximately 1.12. And if 1.12 were the cost for 1 kg of flour, then 24 kg of flour should cost more than $24. But, wait. We already know that the bag of flour costs $21.50. Hopefully they'll arrive at this contradiction on their own, and re-think their question.

We'll then attach the units to the numbers accordingly and let the conversations continue. When kids tell me that they will calculate two numbers using operation w, I always follow up with, What does your answer mean? What unit or units does it carry?

Too often kids have trouble with word problems. Too often they don't know what to do with two numbers let alone a bunch of numbers. They guess at division when one number is big and one is small. They add when they see two fractions. They multiply because that was how they solved the last word problem.

I will also do this with my 8th graders because I suspect they will have trouble too. And this is exactly the kind of trouble we need to get into. Now rather than later. This task gets them thinking about ratios — which is like the most important math thing in all of the math things.

Steward is exactly right about this task. And I'm thankful he shared.

It was used as a fine example of how reversing the question can often lead to a more challenging task.

New Marking Strategy

When grading a 10-point assignment, I have a hard time deciding if the work shown is worth 4, 5, 6, or 7 points. If I like the kid, then I’m giving her a 9. If I’m hungry, then the kids gets a 4. If the kid’s mother gave me a $25 Starbucks gift card, then the kid gets an 8 with a drawn smiley face.

What I end up doing is giving every less-than-complete paper a 1 — yes, ONE — and so far this marking strategy seems to be working.

I want kids to revise their work until it’s flushed with coherent mathematics. A score of only 1 at the top of their paper — along with my comments — motivates them pisses them off so they go back and revise their work. If they need help with the revision, they know where to find me. If the revised work is still not up to par, then the score stays as a 1, and the kid gets to revise it again and again. Or when the grading period ends. And while I haven’t kept track of any hard data, I’m willing to bet that the revision rate has at least doubled.

Grading papers sucks. But grading with a 1 or 10 has alleviated much of the stress. Like I found a cure for my crazies.

Greenies

Our black lab Mandy is 3.5 years old, weighs a ton, and her breath used to smell like death. Until we started giving her one Greenies a day. My husband orders them from Amazon, he also gets them for our neighbor's small dog Bailey.

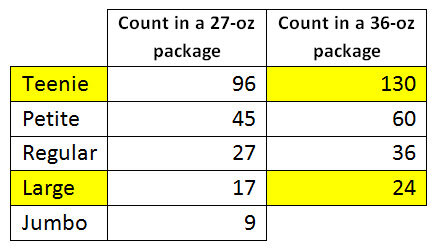
Although both boxes weigh the same 36 ounces, Bailey gets 130 treats in the Teenie size and Mandy gets only 24 in the Large size. This caught my attention which led to this task with my 8th graders who happen to be working with similar shapes. (Like I had planned this all along.)

Greenies are sold in various size packages. I'm interested in the 27-oz and 36-oz.

To launch the task, I hold up the 2 treats: 1 Large and 1 Teenie. I tell them that there are 24 Large ones in a 36-oz package, and I want them I guess how many Teenie ones are in a 36-oz package.

Then I give the students these:

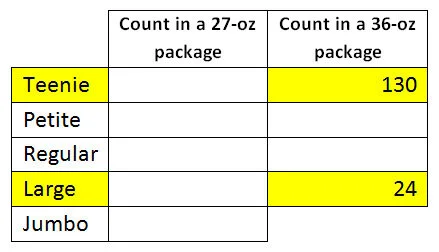
• The photo of the 2 packages (so they know only the highlighted information in the table above).

• Each group of 3 students get two real treats: 1 Large and 1 Teenie.

In return, the students need to give me these:

• A 2-dimensional outline (with dimensions labeled) of what a Petite, a Regular, and a Jumbo may look like. For example, these are the actual outlines of the Large and Teenie. They may write down the thickness also.

• A completed table with the missing counts filled in.

Highlights of this task:

1. Kids use some known information to construct new information. They use modeling to figure out what the other sizes may look like and how many of them would fit in a 27-oz or 36-oz package.

2. It's kinda messy and weird. While the kids can measure whatever lengths of a treat, how do these numbers translate into the mass of each treat?

3. It's good to work with solid objects instead of just flat polygons when learning similar shapes.

4. The reveal (Act 3) of something like this is always a lot of fun. Not only the reveal in the count per package, but also how close their outline sketches are to the actual treats when I bring in the Petite, Regular, and Jumbo.

5. How much does a 36-oz package cost?

6. Is the Jumbo a shot in the dark? Would kids think to ask me for the size of the dogs? How does this help, if at all?

Rigid Transformations

My 8th graders are learning about rigid transformations. I want to add a bit more complexity to what our book is asking the kids to do. For example, the book is having them reflect a shape mainly across the x-axis or y-axis, or on a rare occasion, reflect it across "the horizontal line that goes through y = 3." Well, right before this chapter, we've been working with writing and graphing linear equations, so I want kids to reflect a shape across any line, including one that may cut through the shape itself.

The book surprisingly has very few examples and exercises with rotations. And from what I can find, all these rotations happen about the origin or about a point coinciding with one of the vertices of the shape. Again, I want kids to be able to rotate a shape about any point, including one that's inside the shape. (I used a playing card — number 7 works well because it's asymmetrical — poked my pencil through it as the center of rotation, and turned the card. I think this helps them see what I keep referring to as the pivot or anchor point.)

Then I give each student this task:

• Draw a shape that has between 5 to 8 sides with no curved edges.

• Transform your shape through at least 3 rigid transformations of rotation, translation, and reflection — in any order.

• On grid paper, give your teacher your complete work on this, including the written directions for the transformations.

• On grid paper, give your teacher only the original shape and the written instructions. Your teacher will give this paper to a random classmate to follow your written directions to arrive at the intended location of the final image.

For students who want more challenge, they may ask for a copy that has just the original shape and its final image without the written directions. The task will then be to figure the appropriate transformations that connect the two images.

I really believe that it's good practice to always give kids more than what we believe they can handle. Let kids tell us when it's too much for them — and we find out soon enough. An ounce of struggle on something hard is worth a pound of completion on something easy.