My Other Math Sites
Lessons From the Classroom
My New Way of Solving Systems of Equations
I Googled “system of equations” and took the first one I saw and worked on it.
I was doing something else with number lines when I suddenly realized that using the number line to solve systems is something no one has mentioned before. (A quick Google search didn’t yield anything. To solve for one equation, yes, but not a system.)
We show students various strategies: elimination, graphing, substitution, and eyeballing. I’m not sure why we don’t start with something that students are already familiar with—a number line. We use it to help students count forward and backward, add and subtract, scale, and all the great things related to #clotheslinemath from Kristen and Chris.
The strategy is not necessarily faster or slower than another but is grounded in the important visual. Equally important is the concept of distance on the number line is preserved. If I had abbreviated or eliminated some stuff, I could have done it faster than the work shown above, but I wanted to show you the full process.
Here’s another random one from the Internet and my work.
I get the coefficient of x or y to be the same, and both equations are in standard form.
Place this common term [6y] on the number line.
I see 6y + 6x gets me to 0, so I mark that.
I see 6y - 21x put me at 54; I mark that. (Not to scale.)
The distance between the quantities is 27 x units equals 54, so each x is 2.
I changed 2 to negative 2 because we’re dealing with the number line, and 54 should not be to the left of 0, but it is here, so I need to adjust.
Task First
I shared these two slides in my earliest talks on the need to embed problem solving into the mathematics curriculum.
Of course I wanted to show off. Not because I got first place (totally because I got first place), but because that piece of paper is the only personal possession that says I won something. You’d think my family would put it in frame, but nobody cared so I put a border of Scotch tape around it. Seeing the obvious care in my taping job is both impressive and pathetic.
When it surfaced while I was cleaning out files (the ones that lived in a massive tall ugly metal file cabinet), I immediately questioned its authenticity. The internet came through with this article from Boise State two years prior to the event. Apparently I got to participate because I was in TAG (talented and gifted). You know what’s dumb though? My English teacher transferred me to TAG—a class full of students who were actually talented and gifted—because of my writing. I remember dreading the transfer and telling my teacher, “But… I’m just trying to learn English.”
The now decades old shift from “back to basics” to “problem solving” in school mathematics makes me wonder why we even begin with the basics and fluency as if they were absolute prerequisites to problem solving and reasoning. We don’t do that with other learnings, like riding a bike or making a batch of cookies. We teach writing by having students do three things: 1) write, 2) write some more, 3) don’t stop writing. So when NCTM (1980) stated that problem solving needs to be “the focus of school mathematics,” we each went our separate ways and implemented what we thought that meant.
Our separate ways might be what I read in Chapter 3 of New Directions for Elementary School Mathematics: 1989 Yearbook (Schroeder & Lester, 1989) where teachers’ approaches to problem-solving instruction fall into three categories:
Teaching about problem solving
Teaching for problem solving
Teaching through problem solving
While it is the third approach, teaching through problem solving, that I subscribe to and advocate for, it’d be foolish (perhaps even impossible) to ignore the other two approaches as I believe teaching about and for are byproducts when teaching through. The converse is not true, however, meaning the first two approaches do not yield problem solvers and deep thinkers the same way that teaching about bicycle wheels and chains does not yield bike riding. At least it does not elicit the wind-in-your-hair kinda joy from actual bicycling.
Below is the best evidence I see that we’re not on the same page.
The person tweeted out this reply when Open Up Resources quoted what I’d said in a talk. And what I’d said was to challenge all students, not just a select few, and we shouldn’t equate struggle with arithmetic/computation as an inability to problem solve.
But we can be on the same page, at least be in the same book, with a shared vision that mathematics learning must be inclusive. I wonder if the exactness of math calculation—that 2 + 5 = 7, and 20% of 80 is 16—somehow translated into the perceived need for exactness of math teaching, at least in its sequence. It reminds me of when a teacher observed me facilitate a lesson on stacking cups and was genuinely surprised that I didn’t teach “the y-intercept” prior to this task.
All that to say we should start presentations with a task, best icebreaker I know, even one like this from Thinking Mathematically (Mason, Burton, & Stacey, 1982):
I have just run out of envelopes. How should I make myself one?
Maybe that was a bad example. Hurry before it becomes obsolete like a file folder.
Thinking About Math PDs
I’ve been thinking hard about math PDs in general, like why do we seem to have the same conversations from more than a century ago. In my last talk, I shared a couple lines from J. W. A. Young’s book, 1906:
The question is not how much? but how? The object is mastery… , and not to train the memory, or to ingest a large bulk of mathematical fact and formulas.
Then Herbert Spencer, 1929, stated that:
Rule teaching is now condemned as imparting a merely empirical knowledge—as producing an appearance of understanding without the reality. To give the net product of inquiry, without that inquiry that leads to it, is found to be both enervating and inefficient.
But I and many others have sat through math classes that Young and Herbert spoke of in trepidation. We consumed mathematics passively. We interpreted good grades as sufficient knowledge and understanding. Then we became math teachers and patted ourselves on the back when our students’ test scores rose.
At CAMT in Fort Worth last month, I leaned over to Sara VanDerWerf and said something like, “I know how to solve the whole PD thing… Teachers meet regularly, observe each other teach, debrief, rinse and repeat. You know, lesson study.” Sara agreed wholeheartedly because she is very kind.
When an admin laments her teachers’ excessive direct-teaching methods despite the trainings, I think about food. Just because we appreciate a good dish—can taste the difference between an okay vs. excellent dish—does not mean we know how to make it. We can be shown lots of greats tasks and how to facilitate them, but it’s heavy lifting to be expected to replicate them with our own kids. What’s more, our PDs are made up of math teachers who normally don’t give the genuine and creative incorrect answers that our students would make. We don’t get to practice asking the right questions at the right time.
The whole PD thing has too many moving parts, too many cooks stirring the pot. I don’t believe there’s one best way to teach. Sure, I vote for student-centered and problem-based learning, but these are shifts in practice and not in themselves classroom strategies. Broadly, I can appreciate what what Peter Sullivan has outlined:
The principal is the leader in teacher professional learning.
This learning is long term.
Teacher improvement must be at the center of any initiative.
All teachers already teach as well as they can, so improvement must be driven by new teacher knowledge and attitudes.
Learning improvement is connected to teaching improvement.
I ran across this lovely thing that John Mason said about a brilliant maths teacher as someone who is “learning to balance care for learner(s) and care of mathematics.”
In other news, I’m happy to share that visualpatterns.org got a much needed facelift from my daughter Sabrina who understood what needed to be done and executed beautifully. As I examined the 471 patterns one by one again, I’m flushed with gratitude for the many contributions, from Simon Gregg’s year 5 students (pattern 99) to Jonothon’s numerous submissions, including this one (pattern 404) that others helped me see.
I’m also happy to be working at Amplify. The year went by rather quickly as I did a fair amount of traveling—enough that I had to rehome our 8 chickens. I washed their feet once more before the nice family with two young daughters came to get them. I think chickens are so smart, but then they also step in their own shit without care so I’m not too sure. I cried for days and wished to raise another flock before I died. This was the last egg from one of my babies. I didn’t have the courage to use it for over a month, then I wanted to make pad see ew, so that was that.
That Sinking Feeling
Whoever installed this bathroom sink unit did not use it to wash hands, nor did they use it to rinse out a washcloth. It’s very shallow and the spout is toward the back of the basin. The water inevitably spills onto the back counter, and the washcloth half dangles in the dirty water that hasn’t drained from the shallow sink.
And this entire awful design flaw is not worth talking about until I realize it’s installed in every guest room at this 450-room-plus hotel. How did this happen? How could a mistake like this happen on such a grand scale? How many people used this sink and thought it was functional [which it isn’t], but rather they didn’t speak up, “Whatever, I’m just installing, won’t be staying at this hotel anyway.”
I think of the materials wasted. The time it took to install. The cost. The unnecessary wiping around the sink each time. How the user — of this thing that it was designed for — was ignored.
But the parts are actually fine, right? Good widespread faucet, solid granite countertop, okay-for-washing-small-hands-only sink. Someone just screwed up on the assembly. There should be a guideline that a faucet must be installed so the water flows out at a minimum of three inches from the back edge of the sink.
This whole thing makes me think about a bad curriculum that ends up on students’ desks. How did this happen? How could a mistake like this happen on such a grand scale?
A First Grade Lesson Using Vertical Whiteboards
As we wrapped up our book study of Peter Liljedahl’s Building Thinking Classrooms, and in my role as TOSA (teacher on special assignment) I do not have a classroom of my own, I asked one of our first-grade teachers if I may facilitate a thinking task using vertical whiteboards with her students.
To supplement the teachers’ classrooms with more whiteboard space, I reached out to Wipebook for durable dry-erase chart paper surfaces (with grids on one side!). The reusable Flipcharts they sent were the perfect tool to use over her glass doors and windows! They can easily be removed and reused as many times as you want — an eco-friendly solution to reduce paper waste. Our district has also purchased whiteboard easels with adjustable heights.
The teacher already had her groups paired up with their “thinking partners.” Each whiteboard space was labeled such as “Blue 1 and 2” so the students knew where they would be working.
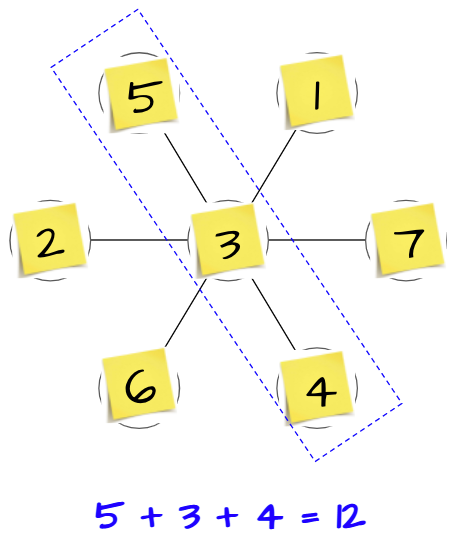
We had the students sitting on the carpet area for me to launch the task. I taped this flower image on the board and asked how many circles they saw. They said seven.
Then, I counted out along with them seven sticky notes, marked from 1 to 7. This great Flower Petal Puzzles thinking task is from Dan Finkel, founder of Math for Love. The intent of the task was for students to write the numbers inside the circles/petals and to keep track of numbers they have used by crossing them off at the bottom of the page. Dan also suggested using counters. However, I wanted the students to do these vertically, so counters would not work, and writing numbers in and erasing them is challenging and cumbersome, especially for young students. The use of sticky notes was really key in helping students stay focused on the task because it was easy to swap out numbers and keep their brains moving.
I called up one student at a time to place a numbered sticky note into an empty petal without further instruction or stating what the goal was. When there was only one space left, I said it was my turn and placed the number in. I wish I had taken a picture of the board at this point. But since I didn’t, below is a picture of the flower with randomly placed numbers. I then told them these three petals are connected and asked them for the sum and wrote the equation.
We found the sum of the other two groups.
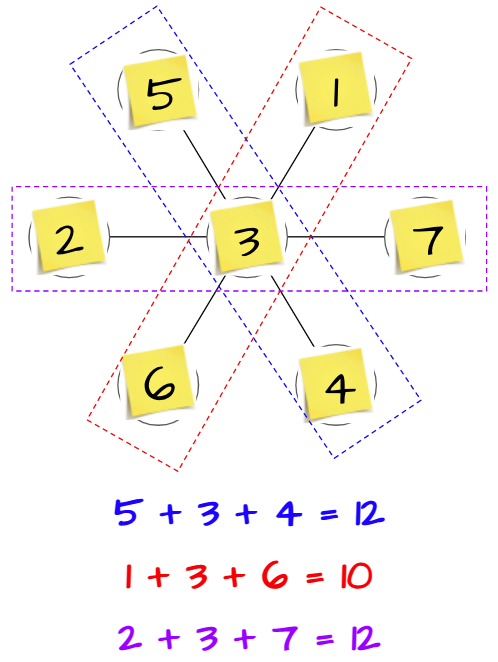
It was not until then that I told them the challenge of the task was to have all three sums be the same. And that the sum is 10. So off they went with their thinking partners to their whiteboards!
Sure enough one pair got the solution within 5 minutes, and we asked them to keep their equations (not erase them), and to do the next challenge which was to get a sum of 12 for all three equations. Some time later, all of the groups except for two got the 10 puzzle. We came over and applauded them for their perseverance and asked if they would like a clue. They nodded and we let them know to place the number 1 at the center of the flower. When this group got the solution with the hint, the girl excitedly said to me, “This is a lot of fun!”
I tweeted this out later as truly it was the best hour with first graders for me. So much perseverance, so much thinking, so much fun. The groups were in different stages (finding sums of 10, 12, and 14), and two groups ended the hour working on the “ultimate challenge” of creating their own puzzle using a 9-petaled flower.
Updated 04/11/2022
I just thought of a way to take this 1st grade task to next level. https://t.co/7vQzKk4kuP
— Fawn Nguyen (@fawnpnguyen) April 1, 2022
7 circles: possible sums r 10, 12, 14 (what #s go in middle circle of these sums, respectively?)
What r possible sums for n (odd) circles? How many equations [of equal sum] for each n?
A Routine for Between 2 Numbers
I hadn’t realized the last few entries of between2numbers.com were left blank. They are done now. Thought I’d share a more revised warmup routine of how I’ve used the contents.
I’ll use entry #1 as an example.
I project the two images only and set the timer for 30 seconds for quiet notice-and-wonder. No writing necessary during this time.
I then say, “Before I show you the speed of each of these, I’d like you to discuss with a neighbor what the numbers might be, let’s think miles per hour.” I ask them to write down their estimates [in a journal]. Set the timer for another minute.
I call randomly on two students to tell the class what their guesses are for the snail. Call on two more students for their guesses for the jet. I record these on the board.
Now I reveal the snail’s rate and ask, “Who has the closest guess to this?” Record their answers. This is a good opportunity for students to check their decimal comparison.
Now I reveal the jet’s rate and ask for the same.
I entertain any other related information at this point. I might ask them if they knew what the average speed of a passenger airplane was. Then, I reveal the question.
Okay, this step is important. It saves time writing and fussing over actual quantities, and I find that it helps students focus on the mathematical operation rather than feel anxious about the numbers. I say, “We’re going to let the snail’s rate be A, the jet’s rate be B, and the distance 2,800 miles be C…”
“... Discuss with your neighbor what calculation(s) you would do to find out how much time it takes each object to travel across the US. Just use the letters now. For example, if you wanted to add the two rates, you’d just write A + B.” Set the timer for one minute.
Randomly call on one group to share. Record on the board what they share and ask, “Who has a different solution?” Write down what they say. Continue asking until I have recorded all the different solutions. (Normally, there are usually just 2 or 3 different ones.)
I now take out a calculator and get an answer for each of the solutions shared. I go back to the owners of each solution and ask, “What unit should your answer have?” (If the units were not mentioned earlier.) We discuss the reasonableness of the correct answer.
I’m proud of this site because the routine affords several of these:
interesting facts
estimating
talking and listening
proportional reasoning
unit rates
dimensional analysis
Here is the key. Please share this resource widely, and if you use it, please let me know how it goes.
Number Talks for Middle Schoolers
If I may recommend only one thing to K-12 classrooms, that thing has to be number talks. As a warm-up routine, it usually takes less than 10 minutes, yet it pays dividends in building number sense, connecting computational strategies, honoring flexible thinking.
I finally finished this set of 90 number talks for middle schoolers — enough for a full school year if you do this routine every other day. But I hope you’ll also share it with your elementary and high school teachers to inspire them to create their own or modify these.
I’ve already shared my notes about the routine on the first 4 slides. I just want to add that each slide — or each group of 3 slides — is intentional, meaning there are several strategies that I hope your students and you will explore and share. My goal is also to tweet these out, one at a time, and include people’s responses on a slide following it.
You know what you should do on the other 90 days. :)
Comparing Fractions
I was taught to find a common denominator when comparing or ordering fractions. Find the LCM. Even change them into decimals.
Instead, I want to compare fractions in these three ways:
Using number sense and the fraction 1/2
Finding a common numerator
Thinking of them as perfect pinks or not
Compare 3/4 and 5/12.
3/4 is more than 1/2, and 5/12 is less than 1/2, hence 3/4 > 5/12.
Compare 1/5 and 2/7.
1/5 is the same as 2/10, and 2/10 is smaller than 2/7 because pizza.
Compare 5/7 and 6/9.
A perfect pink color is made from 1 part red and 2 parts white, expressed as 1/2. I have a visual sense of this color, this red/white ratio of 1/2. Anything greater than 1/2 is dark pink, and anything less is light pink.
So 5/7 is darker, and to get to the color of 6/9, I’d need to do this: 5/7 + 1/2 = 6/9. If I’m adding something less dark than what I’d started with, then I’m going to dilute the color, so 6/9 is less dark than 5/7. I conclude 5/7 > 6/9.
Of course if I add the exact same color to itself, then there should be no change: 2/3 + 2/3 = 4/6.
Compare 19/60 and 21/55.
19/60 is light pink, so is 21/55. To get from 19 to 21, I’d need to add 2 reds, and to get from 60 to 55, I’d take away 5 whites. The net effect is more red, making 21/55 darker, or 19/60 < 21/55.
This is not unlike how batting averages work.
Dear New Teachers
Congratulations! Whether you’re a brand new teacher or you have a new assignment, whether you’re in a new building or you’re returning to the classroom, I wish you all the best.
Take attendance each day out loud. I wish I could take back the days when I just looked at the empty desks to mark down the absentees. I thought I was being efficient. Greet students each day by saying their names and acknowledging their presence:
I’m so glad you’re here.
How was your game yesterday?
Your hair looks great like that.
Thank you for being here.
On days when everyone is present, I add, “Today is perfect already because you’re all here.”
Do math every day, especially on the first day. The kind of math where your students talk in groups for at least 75% of the time. If your principal tells you not to, they are wrong.
If you have plans to ask students to share/write about what they did over the summer, I will just let you know that I dreaded that assignment as a student. My family really didn’t go anywhere; guess we couldn’t afford to. We went nowhere and did nothing. That’s hard to expand on.
Tell your students an everyday story. Did anything happen in the last 24 hours (or over the summer) that you’d want to share? Be spontaneous. Make it quick. How was your dinner? The drive in this morning? Something funny your child/partner had said? This is not something you force or make up. You either have something light to say or you don’t. Here’s mine: Last week I asked my husband to teach me how to dive into the lake from the dock. (No, I had never done this before. I kinda know how to swim, meaning I don’t really know how.) He demonstrated, talking me through the motion. My turn — I assumed the proper dive position — and before I could change my mind, I did a belly flop. He laughed hard and asked me to try again. So, I gave it another shot. And I did it! I perfected the belly flop in my second attempt! My tummy and face hurt from the impact. I’d never seen my husband laugh this hard. He told me I was a champ.
For the longest time I had only two rules to tell my students on the first day of school: 1) never give up, and 2) never tell an answer. I would also tell them where to go should we hear the fire alarm. And that was it. I don’t know what possesses us to inundate students’ first day with a soul-crushing list of rules and procedures. We still have the next 179 days to tell them whatever else we need to tell them.
You can measure the students’ enthusiasm for your class quantitatively: time how fast they arrive at your door the next day. :) What teachers do is really hard, and I hope you’ll reach out to people who have your back. Always make family and yourself a priority. The students and the lessons should bring you joy. If they don’t, I hope you’ve saved up to start a vineyard.
Let’s do this.
Fawn
Fractions Operations Using Rectangles
A few days ago, Mary had replied to Nat’s tweet.
@fawnpnguyen is the queen of this. Pretty sure she has a blog post on it.
— Mary Bourassa (@MaryBourassa) May 14, 2021
God, I love Mary. She sent me a decadent chocolate bar from 2,800 miles away. She remembers my birthday when 2/3 of my children did not.
I am queen only in my own head, and no, I did not have a blog post on adding fractions. I thought surely there must be a wide assortment of videos on adding fractions using rectangles. But the very first two that I’d clicked on - this and this - really astonished me. They both used grid papers without using the grids. Like, what the heck.
Say we want to add 2/3 and 4/5, same two fractions that popped in my head when I replied to Mary.
Draw two same-size rectangles using the denominators as dimensions.
Students will ask, “Why 3 by 5?” If they don’t, you ask why. And you answer them by asking them to shade in 2/3 for one rectangle and 4/5 for the other. Give them a few seconds to do this and they’ll understand why the 3 by 5 rectangles work pretty well here.
We’re adding the fractions, so let’s combine them.
Similarly with subtraction of fractions.
For multiplication, the word “of” is useful. Of course, the commutative property of multiplication applies too.
To take 2/3 of 4/5, we’d look along the height in this rectangle as we can see the thirds and just grab two of the sections.
Likewise, taking 4/5 of 2/3 is to look along the width of 5 and grab 4 sections of it.
I’ve written about division of fractions previously: