My Other Math Sites
Lessons From the Classroom
Green Olives
My 7th graders are working on "percentages of" problems currently, and late last night, I saw this problem on one of Don Steward's handouts.
There are 75 olives, 40% of which are green. I eat some of the green olives until 10% of the olives that remain are green. How many green olives did I eat?
How would you solve this? I solved it using algebra. Then, immediately, I thought, Fawnzie, since when do you use algebra to solve stuff like this. C'mon, do your rectangles.
I think of 40% as 2 of 5 boxes.
So, 75 olives must split into 5 groups of 15, so there are 30 green olives.
Then, I ate some olives to end up with only 10% of the remaining olives are green.
Well, since I didn't eat any of the 45 black olives, so these 45 must make up 90% of the olives remaining [in the 9 boxes], so 45 must split into 9 groups of 5.
Oh, look! I began with 30 green olives, I now only have 5 green ones left, so I must have eaten 25 of them.Okay, your turn.
There are 80 olives, 75% of which are green. I eat some of the green olives until 20% of the remaining olives are green. How many green olives did I eat?
I’d rather use the drawings than show them my work below.
Long Live the #MTBoS!
Dan Meyer is calling for the retirement of the hashtag #MTBoS. He’s suggesting and going with #iteachmath or #iteachmaths instead.
I get it. I get it that #iteachmath means I TEACH MATH. I get it that #MTBoS could mean anything. I get it that Dan’s intention is no more than to simply make the math community more inviting and inclusive. After all, Dan is among the first handful of math bloggers who helped transform my teaching, and he continues to inspire and challenge my craft. I’m grateful for Dan’s work.
What I don’t get is folks saying #MTBoS is exclusive and alienating and cliquish.
This kind of statement actually hurts my feelings, like someone just said something negative about my children without ever having met them. I feel hurt and insulted because the #MTBoS that I am grateful to be a part of and the people who are in it are anything but “alienating” and “cliquish.”
That’s because I know of the ENORMOUS amount of TIME, WORK, and LOVE that had been poured into making #MTBoS what it is today.
Don’t know what #MTBoS is? Please start here: https://exploremtbos.wordpress.com.
When you’re done there, please see here: http://www.fishing4tech.com/mtbos.html.
It takes ONE click to learn what #MTBoS is.
Anna Vance’s tweet exactly expresses how I feel.
I'm not kidding when I say that you all are part of my family, that is how I think of the #MTBoS . It's forming relationships w/ each other
— Anna Vance (@TypeAMathLand) July 28, 2017
Euclid's Algorithm
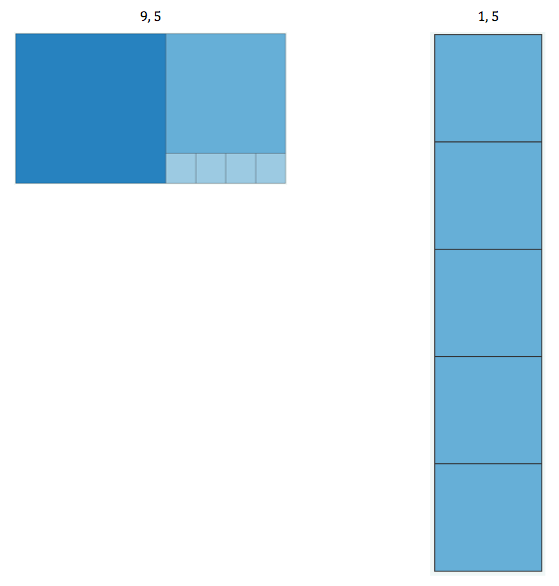
I show my 6th graders this image, pointing out that this picture represents the two numbers 1 and 1 that I'd entered at the top.
I then ask them to give me two new numbers — any two positive integers [that are 10 or less, for now] — and the computer will draw a new picture. As each set of new numbers is entered and the corresponding picture is generated on the screen, I ask students to jot down their "I notice, I wonder" in Google Form and to draw a rough sketch of it in their journal. After a few sets of numbers, I ask students to imagine and/or draw a rough sketch of what they think the picture will look like before I hit the update button.
These are the pairs of numbers they'd asked for and their corresponding pictures, listed in the order that was asked.
I love that the kids are asking for...
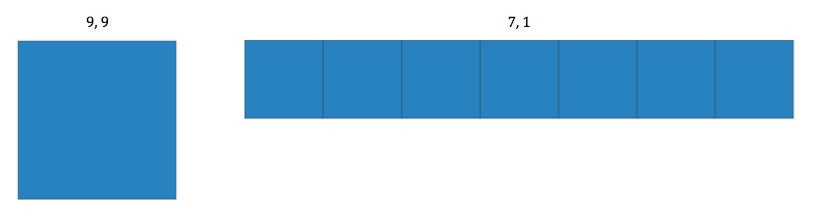
6, 6 after the initial 1, 1
3, 8 after 3, 1
8, 3 after 3, 8
But, when sets 9, 9, and 7, 1 are asked at the end there, I say to the class, “Hey, what if figuring out this puzzle — which is how the computer draws the picture given two numbers — gets you a million dollars. And you get to ask for sample sketches like you've been asking, except that each sample costs you some money! So, make each request worth it. Let it prove or disprove your conjecture. Ask carefully."
I love the OHHHs and AHHHs after each picture is revealed. But no one is claiming that he/she had drawn the same diagram. I pause longer for them to write down their noticing and wondering.
I now say, "You may only ask for four more sets of numbers. Remember, make a request that would test your conjecture."
I ask a normally quiet student. She says, "10, 3."
Another student wants to know what "100, 5" looks like.
"What about 8, 5?" I reply, "Sure, but draw it in your journal first." They are fully engaged. Then I say, "Now, share your drawing with a neighbor."
I ask, "Did anyone sketch the same thing as their neighbor?" They're shaking their heads, and I say, "That's pretty crazy! Do you think yours is more 'correct' than your neighbor's?"
I reveal 8, 5.
The last request is 23, 75.
What some of them have written [with minor edits from me]:
When we did the same two numbers the shape didn't change but when we did different numbers it changed. Why does it divide into little parts within a square when we put 3,8? When we did 8,3 the number switched around. I wonder if the two numbers are dividing to make the shape. How can you figure out the number when it can't divide easily. My drawing for 8,5 was one whole and 5 little squares. The 23,75 was a little confusing to me.
They're different, they are the length and width, and when the two numbers are the same it's just one cube. I notice that if it can be simplified, it is. Example: 6,2 = 3,1. I don't understand 8,3, 5,9, 23,75 or 8,5. But I did notice that the smaller the parts of the shape are, the lighter shade of blue they are.
I observe that when the same numbers are entered it equals to a blue square. If the first number is bigger than 2 then it will add one more square. I wonder if you double the number for each number will it be the same shape. I wonder why for 3,8 it has one square with three parts. I observed that if you divided the first number by the second it will equal to the number of squares. For 8,5 I didn't get the right sketch. The sketch was one square with half of a square cut in half, then in one half is has a strip that is cut in half. I wonder why it has half of a square. I think that my answer for how it figures it out is right, but I don't know how it comes up with that picture for 8,5.
When you do 1 and 1 it doesn't change because we tried 6 and 6 it didn't change and if we put 3 and 1 it did change. I saw that when we did any number like 3 and 1 is 3 ones. So I think that all you have to do is divide something by something = the first number that you put in but if you can't divide by 2 then I'm wrong. I'm not sure that I got this right but this is what I think.
For the first one 1 and 1 I thought it would be a small one by one cube. What threw my off was the 6 by 6 because the size did not change. For the 8 and 5 I drew a big block and and 5 little ones, but my image was wrong. I also wondered if the first number was the amount of shapes that would appear, but I was wrong again. I don't understand yet. I tried looking for a pattern, but couldn't find one.
When I tried 8,5, my answer was almost right. I had the one big square right, the half square right, but then I got the little squares wrong. I think that the way the computer does it is dividing the first number by the second number. I am confident that if you put the numbers 10 and 5 in, it will show 2 squares. When using the diagram, the second number will represent the vertical side.
What I've been noticing was that if you put the bigger # in the front and the small # last then it would be like a rectangle. I've also been noticing that if you put the same #'s it would like keep on drawing a square. So someone said what could (8,5) look like and Ms.Nguyen showed us the drawing and the I notice that nobody got it right. I was expecting something like smaller because the #'s were small they weren't as big, but at least I tried to get it correct but I drew something a little bit smaller than that. I also wondered why when we put the same #'s together why do they all become a square that's what I wonder.
For 5, 12 I notice that it is two big squares, two smaller squares, and two tiny squares, I thought it was going to show 1 big block and another big block but that one would be cut off at the bottom or not a whole block. I also notice that the pattern is the first number multiplied by what equals the second number and the number that is missing is the amount of blocks that is created. I thought I knew it but I don't really get the ones with a bigger number first and the smaller one last. I thought I knew what 9, 23 was going to be but it the result was surprising. It didn't look at all how I thought it was going to. The website is pretty cool, but one thing I didn't understand was the placement of the small blocks and what they stand for. Like some were really tiny and some were small but I don't know what they stand for. But I bet if someone explains it to me I probably will understand perfectly and feel dumb.
The only thing that I am sure that I know is that when the first number is larger than the second, the shape is wide and when the second number is larger, the shape is tall. Other than that I am very confused.
Then, together as a whole class, they agree on the following;
When both numbers are the same, then the picture is one square.
The computer simplifies the two numbers, such that a picture for 6, 3 is the same for 2, 1.
When the second number is a 1, then the picture shows the first number of squares. For example, 7 and 1 would form a picture of 7 squares, and 100 and 1 would form 100 squares.
The first number is the horizontal dimension, while the second is the vertical.
They are all squares.
The dismissal bell is about to ring, and I want to teach forever.
Tomorrow, we'll spend some time with one set of numbers, like 10, 3 or 8, 5. We'll dissect the diagram. Play around with a few more. Practice sketching a few. We'll write out the equations that go with each diagram. I'll guide them into noticing the size of the smallest square in relation to the two numbers.
I found this investigation at underground mathematics. The site describes itself as having "rich resources for teaching A level mathematics." From what I understand, "A level" means advanced level mathematics consisting of core modules ranging from quadratic, logarithms, geometric/arithmetic series, differentiation/integration, etc.
Perfect for my 6th graders who continue to torment me with their arithmetic atrocities, such as, 3² = 6 and 5 ÷ 10 = 2.
While the original task is scripted for older and more advanced students, I found in it what I needed to make it rich and appropriately complex for my 6th graders.
Hail, Euclid's algorithm!
Solving an Equation With a Fraction
From CPM:
The Sutton family took a trip to see the mountains in Rocky Mountain National Park. Linda and her brother, Lee, kept asking, “Are we there yet?” At one point, their mother answered, “No, but what I can tell you is that we have driven 100 miles and we are about 2/5 of the way there.”Linda turned to Lee and asked, “How long is this trip, anyway?” They each started thinking about whether they could determine the length of the trip from the information they were given.
And I like both methods, especially Linda's.
Without using a visual, we may have students solve for x in the equation (2/5)(x) = 100 by multiplying both sides by 5/2.
But I notice two things: 1) Students don't always remember why they are multiplying by the reciprocal, and 2) Students have difficulty showing Linda's method with an equation like (9/2)(x) = 27.
So, I'm having the students think through the problem by answering these two questions:
If we know that nine halves of x is 27, then what is one half of x?
Now that we know what one half of x is, what is a whole x?
As we write the fractions, we can keep our focus on the whole number numerator and treat the denominator as if it were a thing, and that thing is not changing.
Another example,
This helps us go back to finding the unit rate in the first step via division, and then find a multiple of that unit rate via multiplication.
Once students make sense of these two steps and become fluent in solving for a whole x, then they can work on the not-so-friendly equations — such as (5/6)(x) = 4 — because they are more confident and trust the process.
Sure, multiplying by the reciprocal would have solved for x in one step, but there's something uniquely comforting to students when they can first find just one part of something.