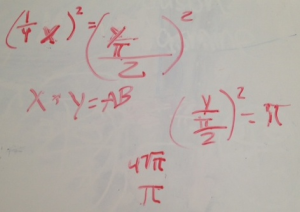My Other Math Sites
Lessons From the Classroom
Pacing Guide
For someone who has openly admitted to not following curriculum pacing guides, I sure spent a ridiculous amount of time churning one out. Our middle school is adopting CPM Core Connections 1, 2, and 3. Aside from our own reviews, the decision to go with CPM were also based on:
Desmos is embedded in many lessons
Other teachers' reviews, including Riley Lark's
I don't know if this would be of any use to you, but I might as well share the doc math 8 pacing 2014-2015. It's kinda pretty.
I replicate our school calendar and put in all the holidays and half-days. I go to each chapter in CPM and write down the guiding questions. Matching up the standards to each chapter was a pain in the ass. (CPM does it the other way around: they have the standards in one column and the different lessons that cover those standards in another.) The suggested number of days for each chapter does not include assessments, so I add about 6 days on top of whatever CPM recommended. I'm going to post the pacing guide near my desk — probably the only document I will print in full color this school year.
(Oh, I took out Chapter 1 because it's on problem solving. C'mon, I got this.)
Then I'm going supplement it like crazy. I can't teach straight from the textbook. Just can't. So the 6 days that I add to each chapter will hopefully allow us some wiggle room to do other stuff.
Other stuff includes, but not limited to, what you see on the right sidebar of my blog.
We also need time to begin each class period with math talks because it was one of the most powerful things we did last year. (Grrrrr. Just realized that most of the images on the math talks site are not there. Why now.)
I was brainstorming with a couple of 6th grade math teachers at another district, and we were listing out a possible warm-up/math talk schedule, something like:
Monday: number talk (spreadsheet that you can take from and add to)
Tuesday: visual pattern
Wednesday: estimation 180
Thursday: fun fact, or WYR, or Keeping Skills Sharp, or SBAC/review question
Friday: personal reflection
My assignment this year looks almost like last year's: 2 sections of Math 6, 1 section of Math 8, and 1 section of Geometry [1].
I wish you a healthy school year. Teach what you love and love the kids. Follow the rules, but break a few if doing so makes it better for the kids.
[1] I'm happy to say that we will no longer be tracking kids in math. However, we need to finish out what we'd started with these 8th graders who took Algebra last year as 7th graders. So this group will do some geometry, some stats, and a whole lot of problem solving.
Come and Observe
I don’t know what else to do except to suggest to an anti-Common Core parent to come and visit my classroom. Visit for a period or stay for the day. Come back again the next day. Stay for a week. Come back again next month. Become a parent volunteer in my room. Help me help a child because God knows we all have children in our room who could use some one-on-one support.
Parents should be our allies. A few are crazy. But there are a few teachers, doctors, plumbers, postal workers who are crazy too. Parents love their kids and want what’s best for them. They are concerned that their kids won’t be developmentally ready for Common Core (CC). They fear that it’s one-size-fits-all, that CC controls kids’ minds and stifle their creativity, that national testing and national curriculum will soon follow. The list of concerns just keeps piling up.
Both sides are quite passionate and create a lot of noise. I engage very little in this noise because I feel my energy in doing so does not get converted into anything useful. It dissipates too quickly, leaving me hollow and out of breath. But I’m talking now by writing. It’s midnight and really quiet here.
I want parents to observe their children do Taco Cart and Always, Sometimes, and Never. I want them to listen in on the kids’ math talks. I want them to walk in on a day when I’m doing direct instruction — and observe how much the kids direct their own learning, how much they try to make sense of something new.
I want parents to observe you — my local and online colleagues whose lessons I steal from and whose support only makes me work harder.
So, that’s my plan. I will invite my parents to visit my classroom whenever they want (I actually prefer unannounced) and see how a CC lesson plays out. The worst that can happen is I fail miserably. But I guarantee their kid will not.
I found some very old arithmetic textbooks, dating back to the 1800’s at Open Library.
Bonnycastle, John. Arithmetic… 17th ed. London: Longman, 1843. Print
These prefaces are quite remarkable. I’ll just share from two textbooks.
Adams, D. (1848). Arithmetic: in which the principles of operating by numbers are analytically explained and synthetically applied : illustrated by copious examples : designed for the use of schools and academies (Rev. ed.). Keene, N.H.: J.H. Spalter & Co..
Exertion, then, to bring teachers to a higher standard, will be more effective in improving school education, than any efforts at improving school books can possibly be. It is here where the great improvement in must be sought. Without the cooperation of competent teachers, the greatest excellences in any book will remain unnoticed, and unimproved. Pupils will frequently complain that they have never found one that could explain some particular thing, of which a full explanation is given in the book which they have ever used, and their attention only needed to have been called to the explanation.
Colburn, D. P. (1862). Arithmetic and its applications: designed as a text book for common schools, high schools, and academies. Phililadelphia: H. Cowperthwait & Co..
In the first place, such tests are unpractical, for they can never be resorted to in the problems of real life. What merchant ever thinks of looking in a text book or a key, or of relying on his neighbor, …?
When a pupil, having left the school room, performs a problem of real life, how anxious is he to know whether his result is correct! Neither text book nor key can aid him now, and he is forced to rely on himself and his own investigations to determine the truth or the falsity of his work. If he must always do this in real life, and if his school course is to be a preparation for the duties of real life, ought he not to do it as a learner in school? Is it right to lead him to rely on such false tests?
Besides, the labor of proving an operation is usually as valuable arithmetical work as was the labor of performing it, and it will oftentimes make a process or solution appear perfectly simple and clear, when it would otherwise have seemed obscure and complicated.
But some of the exercise problems are just insane. I intentionally looked only for exercises in division of whole numbers. And all these textbooks were for school-aged children, grades 4 through 8.
1909, Walton & Holmes:
408903 ÷ 3508
147500 ÷ 6190
1921, Thorndike:
748275 ÷ 825
42974 ÷ 8523
1862, Colburn:
55673 ÷ 6349
2700684 ÷ 19743
1848, Adams:
46720367 ÷ 4200000
reduce to lowest terms: 468/1184
1843, Bonnycastle:
4637064283 ÷ 57606
Common Core looks better than this.
MathEd Out Podcast
Adrian Pumphrey was very kind and patient when he interviewed me for this month’s MathEd Out podcast.
Other folks whom Adrian had interviewed thus far:
Julie Reulbach — blogs at I Speak Math
Dan Meyer — blogs at dy/dan
Lynne McClure — Director of NRich
Daniel Schneider — blogs at Mathy McMatherson
Sue VanHattum — blogs at Math Mama Writes
Upcoming interviews:
Bill McCallum — Lead author of CCSS
James Grime — Numberphile
Malcolm Swan — MARS
Thank you, Adrian, for the honor and pleasure to do this. I’m really bummed that I won’t be at #TMC14 to meet you in person.
The Right Question Institute
From www.aish.com:
Isidore Rabi, winner of a Nobel Prize for physics, was once asked why he became a scientist. He replied: “My mother made me a scientist without ever knowing it. Every other child would come back from school and be asked, ‘What did you learn today?’ But my mother used to say, ‘Izzy, did you ask a good question today?’ That made the difference. Asking good questions made me into a scientist.”
A week ago my superintendent, principal, and 7 of us teachers attended a full day workshop The Right Question Institute in LA. Luz Santana and Dan Rothstein, authors of Make Just One Change, facilitated a worthwhile and engaging session, so I just want to share some highlights and my takeaways from it.
Highlights
(Some of these might be direct quotes. I’m just writing from my notes.)
Not knowing what to ask is the fundamental obstacle to participating and therefore to learning.
The skill of question formulation is the single most powerful renewable source of intellectual energy.
How can we easily develop students’ question formulation skills? It’s simple. But simple does not mean simplistic — it means doing it so everyone can access it.
Six components of the Question Formulation Technique (QFT):
A question focus — the teacher gives a prompt related to topic currently being covered in class, prompt can be visual. It should be a statement or phrase and not as a question. The simpler, the better.
Producing questions — in small groups, students share questions that they have related to the question focus (prompt), one person records on large poster paper or whiteboard. But before starting, everyone is reminded of these rules:
Ask as many questions as you can.
Do not stop to discuss, judge, or answer any question.
Write down every question exactly as it is stated.
Change any statements into questions.
Categorizing questions as “open” or “closed.”
Prioritizing questions — choose 3 most important questions from list, pay attention to the question focus.
Next steps — what’s one way you could use your priority questions?
Reflecting — what did you learn and how did you learn it?
Takeaways
Luz and Dan are really lovely people. Warm, hard-working, fun. Their book — and this Institute — mark the arrival of a twenty-year journey for them! (Arrived, yes. Settled, no.)
This task of having kids ask their own questions is not unlike Act 1 of a 3-Act math task that many of us are familiar with.
But the QFT process can be used — and is used — in a variety of academic disciplines and in communities outside of school. (Their journey actually began when they worked on a dropout prevention project and heard from the parents who were not coming to the school meetings because they “don’t even know what to ask.”)
This is another powerful structure that empowers students when asking questions becomes a natural tool for them. They think more critically because the QFT process helps them hone in on their questions. Dan and Luz categorize the learning of asking questions as going from divergent thinking to convergent thinking, then that last component of reflecting is metacognitive thinking.
Teachers and students will get better at implementing the QFT. It’s building classroom culture, so it takes time.
We’re doing this already with our students to some degree with varying expertise. Maybe we just need to be more intentional about it. Give it a name.
If not, perhaps Make Just One Change.
What Our Students Thought of Ability Grouping
A month ago I wrote about Ability Grouping and within that week asked my students for their thoughts, but I've been swamped with work to share any sooner. My teaching assignment was:
Geometry: 32 students. All were 8th graders, largest group we'd ever had, 45% more than the year before. A handful of them were not ready for the rigors of this high-school equivalent course; it was more due to scheduling that they ended up here. (We have about 200 kids in the junior high, 2 sections of each level, so it's not easy to be flexible with our schedule.)
Algebra 1: 38 students. Ten were 7th graders, the rest were 8th graders, and 3 of the 8th graders worked independently out of the Algebra Readiness textbook at midyear as they struggled to continue on, but they joined the rest of the class for all problem-solving group tasks which happened about twice a week.
Math 6: 69 students in two classes, but 2 of them were in RSP for math, so I only saw them on Fridays.
My colleague Erin helped me give her students the same survey questions. I don't know her exact roster counts, but she taught two classes of Pre-Algebra (all were 7th graders) and one class of Algebra Readiness to 8th graders. I began by telling the kids a little bit about ability grouping at our school, that it existed in grade 7 and grade 8, that we tried to place them based on several measures (grades, work habits, CST scores, benchmark tests). I did not tell them how I felt previously or presently about ability grouping, but I wanted to learn what they'd thought. I gave each student this strip of paper and asked them to check one box.I then added these three questions: I'm going to summarize what boxes the kids checked for both parts above like this:
From the Geometry kids (there was some city-level academic competition going on that day, so more absences than usual):
From the Algebra 1 kids:
From the Algebra Readiness kids:
From the Pre-Algebra kids:
From the 6th Graders:
So, about 83% (151/183) of the kids said YES to ability grouping. Sure, there were a few kids who seemed to have conflicting responses by checking NO to the first question but had more YES responses with the 3 questions that followed, and vice versa. I don't know. I do know this: Erin and I really love our students and love what we do. She has a math degree, I do not, but we both love problem solving and are proud math enthusiasts. She let me talk her into going for a week-long training in Palo Alto to jump start — actually it was more of a revival of — a Math Teachers' Circle in our area. I want to believe that Erin and I made a difference in how our students felt about their learning of mathematics. Doug left a comment on my Ability Grouping post. His last paragraph strikes the perfect note of what I want to say right now:
I wonder if the bigger problem is teaching students to not be so concerned with who is "ahead" of whom. Maybe the problem has less to do with what class you put the students in, and more to do with how you treat them once they get there. We need to foster the growth mindset. Maybe our fixed-ability mindset (ala Carol Dweck etc.) primes us to be unnaturally sensitive about placement. Most of us will live and die always knowing there is someone, lots of people, more competent/talented/accomplished than we are at everything we do. But we have to live for ourselves, and pursue what we care about, regardless. The bigger issue is making sure every classroom has a good teacher presenting quality material. Then it doesn't matter who is in what room with whom.
Thank you, Doug.
Playing With Math: Stories From Math Circles, Homeschoolers, and Passionate Teachers
Sue VanHattum's blog Math Mama Writes was one of the earliest math blogs I frequented. Sue and Shireen, Dan, Kate, and Sam were among the first people who showed me — through their passionate writing — that there was an online community where we may share the teaching and learning of mathematics in the classroom.
When I started this blog, Sue dropped in to leave a comment or two. Or five. We even talked on the phone, and she shared with me how her son got his name. I remember reading someone's post and wanting to leave a comment because I connected with the piece and its author in some small way, and inevitably I would find that Sue had already left a comment. This happened over and over again. I felt we were reading the same stuff; and the same stuff touched us in similar ways.
Then, within a year Sue asked if I would like one of my posts to appear in a book she was putting together.
So, it's with much love and honor that I get to help launch Sue's new book:
Playing With Math: Stories from Math Circles, Homeschoolers, and Passionate Teachers brings together the stories of over thirty authors who share their math enthusiasm with their communities, families, or students. After every chapter is a puzzle, game, or activity to get you and your kids playing with math too.
To know Sue is to know that she loves teaching and learning mathematics, and she loves writing, therefore this book — this work of consummate love - has to happen.
Playing With Math is really a collection of love stories because the authors, including yours truly, want to share something we're pretty crazy about. It's the stuff we do beyond the regular school day — we play with math after hours, at the dinner table, on a napkin at the coffee shop, with our own child or with a neighbor's child, at a family picnic, with our in-laws whom we don't even like.
So, today is the first day of our crowd-funding campaign to cover production costs. We're hoping to find support in our community of teachers and parents and math connoisseurs — a community of people whom I adore and respect. You can contribute anything from $1 to $1 billion. But for a contribution of $25, this wonderful book will be sent to you as soon as it's printed. Please see more details here.
Thank you so very much.
Mindset
I’m very grateful to be here at the 3-day MAP Conference in South San Francisco — finally got to meet Malcolm Swan whose lessons I’ve used with my students for many years. I was delighted to see this slide because we did this lesson and it was one of my favorites.
At the end of today's session, we were asked to share questions that we may have for tomorrow's panel of speakers. A teacher asked this question, and it stayed with me. He said something like this:
The students in the video [during Malcolm's talk] are awesome. But my students are not there. They are at zero. Not even zero, they are at negative something...
Negative?? Zero?? It made me sad to hear this. No matter how "low" his students are, no matter how out-of-control they appear, no matter how unmotivated they seem, they cannot be at level zero. That's impossible. We talk a lot about students' mindsets. I worry more about the teacher's mindset. Maybe this teacher didn't mean it the way I'd heard it; but I've heard teachers say directly to me, "My kids can't do that." How do we know that unless we give them a chance.
Discount and Sales Tax
Instead of doing the above exercises in our textbook, I had my 6th graders do this:
Shopping Contest at Target
Let’s pretend Target has a contest. The contest is for shoppers to find merchandise from their online store.
Contest rules
You must choose at least 10 different items.
The items must come from at least 5 different departments, such as footwear, kitchen, clothing, toys, etc.
You may buy more than 1 same item — you can buy 2 or more packs of athletic socks.
The winner
The winner is the shopper whose merchandise receipt totals exactly $500 or closest to it — without going over. They get to keep all the merchandise!
Your task
Phase 1: Go to Target’s website and find some items that you’ll want to get for yourself and your family. List the items and their original prices in the table provided separately.
Phase 2: The store manager (really, it’s your teacher) then announces the percent discounts for different categories of merchandise. Write these down below. Apply these discounts to your items and calculate the new sale prices.
Phase 3: The current tax rate for our city is 8%, so you must add this to your total. In this phase, you get to add or remove items on your shopping list to reach the target goal of $500 without going over.
I only did Phase 1 with the kids, my sub supposedly did Phases 2 and 3 with them. (I wanted to do the rest of the lesson with them when I return from NCTM — and after spring break — but they voted to continue the lesson with the sub as they were really into the task. I'll find out tomorrow when class resumes.)
Why this task
You can change everything about it. Shop somewhere else instead of Target.
Change the rules depending on time available and access to computers. Are there enough computers for each kid or do they need to work in groups of 2 or 3? My kids were in pairs. (We have enough laptops, but at least 30% of them have issues.)
I like the idea of not going over a certain amount — $500 in this case — instead of "whoever is closest to the target price" because I think it keeps the kids more reserved in their shopping spree. Students understand that if there were only 2 contestants, then the one with a final receipt total of $154 would win over the other with a $501 total.
Kids don't know what the exact discounts are until Phase 2, so this makes it a fun temporary secret. But they know to go over budget in Phase 1 because there will be discounts — not all departments have to have discounts either. Their totals in Phase 1 were in the $600 to $700 range because they also know that it'd be easier (faster) to remove items than add them later in Phase 3. They were also told that the discounts would be somewhat realistic, meaning Electronics will get a smaller percent discount, if any, than Clothing.
They'll become more aware of how much things cost — and how quickly they add up in the shopping cart.
Handout Discount and Sales Tax
Prices, Proportions, Percents
I was in Garden Grove with my son on Sunday, and he insisted that I try this smoothie place called Tastea. With Jamba Juice and Blenders and all the other juice bars around town, I was skeptical that this joint's concoctions would be anything different. He ordered a taro milk tea and I got a Thai tea, both with boba. Just one sip and I said to him, "Let's order another round! It's a long drive home!" Soooo delicious.
While there I saw a math lesson brewing, so I picked up their menu with prices. This is the lesson with my two classes of 6th graders.
Me: (I tell them about Tastea and how I wish it were closer.) Okay, let's start with something you might be more familiar with, Starbucks. I love that now I live within walking distance from one! Do you know the different sizes that they have there?
Class: (When I refer to "class," I don't mean the whole class, of course, but somebody in the class joins in on the conversation.) Tall, grande, venti.
M: Do you know exactly how much liquid each size holds? (They make various guesses. I bring out the 3 sizes that I got from Starbucks so they have a visual.) I normally order a tall mocha frappuccino, let's say the price is $3.50. Do you think the venti, which is twice the volume of the tall, would cost twice as much, or $7.00?
C: No.
M: Why not?
C: You normally get a better deal with a bigger size.
M: What do you mean by a "better deal"?
C: (All their answers show me that they understand the idea of more bang for your buck. Then finally someone says...) Lowest unit price!
M: Right! That's why so many families go to Costco. Buying in bulk normally saves us money because the item has the best unit price. Well, we're talking about Starbucks now, so buying more is a better deal, but drinking more is not so good for our body. Let's fill in this sheet. (I pass out this handout. And here’s the key.) How do we calculate unit price? What place value should we round it to? How do you write thirty-one-cents-per-ounce?
M: Tastea has three sizes: mini, gigantic, and even more. Their teas can also be purchased by the "partea jug," which holds a gallon. I've given you the prices of the 10-ounce minis for the three different types of drinks, your job is to figure out the prices of the other sizes. You'll work in small groups to figure out these out. So, do you think the gigantic will cost twice as much as the mini because it holds twice as much?
C: No. It'll cost less.
M: How much less? Well, that's your group's job to come up with the best estimate. We have Starbucks' prices for their three sizes, you could look at how they price their drinks. But here's the sweet deal for you. You and your group mates do the math that you need to, then write down your first estimation right here in this column. Bring your paper up to me (only the "captain's" paper), give me a few seconds to figure out the percentage that your estimation is off by, and I'll write it in this column and give you back your paper. What percent do you want to see, large or small? What if your estimation were the actual price — what percent would I write there?
I tell them that they could figure out the actual price of the drink if they knew how I calculated the percentage of error. So, work work work. Think think think. What makes sense? Oh, I remind them that the percentage does not indicate if their estimation is too high or too low. So, again, what makes sense?
We also note that prices generally end in a 0, 5, or 9. So, even if the calculation tells them the price should be $4.23, they might want to change that to $4.25 or $4.20.
When they bring up their paper again with the second estimation, all I do is write their estimation again in pen and circle it — this is so they can't change their answer and I know that I've seen it. I do NOT fill in the "Actual Price" column at this time because the groups are working at different rates, and in a crowded room, it's easy for kids to see each other's papers, even inadvertently, and the game of estimation is over if they saw the actual price beforehand.
They simply move on to the next size to make a first estimation again. We repeat the process.
When all groups are done with estimations for the first type of juice — smoothies — I tell them what the actual prices are.
Now, it's their turn to figure out the percentage of error. I give the groups about 10 minutes to do so without help from me. At the end of the 10 minutes, either there's at least one group that knows how to do so and can show it to the class, or no group knows how, then I'll walk them through the calculation by asking them questions to figure this out.
They continue in the same manner for the Slushy Freeze and Specialteas on page 2. This time hopefully they'll be able to work backward from the error percentage that I give them after their first estimation.
Reasons I'm proud of this lesson:
It's about proportions, but many priced items in real life are not directly proportional. The kids knew this coming in because they've been consumers.
We get to talk about business strategies that entice people to buy the larger sizes while still make a profit. (Starbucks calls it "tall" because it rhymes with "small," but clearly the word tall naturally elongates the imagination.)
Students get to make estimations throughout, but they know these aren't "wild-ass guesses." They start with the calculation of proportions and adjust the prices accordingly. They get to critique and argue with their group mates to come up with the best estimations.
I get kids to think about percentage in a context that they can wrap their heads around. And they want to know how because their second estimation could be dead on if they knew.
It's fun that the error percentage does not indicate if their estimation is too high or too low. A few groups do go farther in the wrong direction. Oh, well — good to learn that now.
It'd be fun for me to get Starbucks or Jamba Juice for the group with the lowest total in percentage errors.
Updated 04/05/14
I got some thoughtful reflections on this lesson, I'll just share two:
I learned how to work backwards with percentages and try to get the number spot on. I also learned how business would price things by dropping the price by the perfect amount. My number sense got a lot better from all the multiplying, dividing, and reasoning. It was very difficult, which I'm very happy about. The teamwork was probably the hardest part of the project. M and I are very competitive, and we got different answers a lot. I learned how to work together with others a lot better, and it doesn't move your team along to place blame and argue. I'm really grateful we did this project because it was very hard and worthwhile. It was a great use of three days!
I learned how to use different data to get answers. Also, we have to see a pattern. This Tastea assignment was really fun. I enjoyed it and look forward to another. Teamwork is really important even though people can't agree, you got to support it. If your group gets it wrong, but your answer was right, you can't blame someone or put them down because probably they will get some right for you. So always stay positive to your teammates and encourage them.
What the Kids Thought
Recently Dan Meyer asks Mathalicious which of these three questions is "real world"?
Karim Ani, founder of Mathalicious, and others have opined without consensus on this particular question and on the general notion of real-world vs. fake-world problems.
I wonder what my 8th grade geometry kids think of this question.
I give them Version A on a strip of paper and ask them to work on it alone for 5 minutes. I tell them that I'm interested in learning if they understand the question as is, therefore I'm not answering any clarifying questions about it. After the 5 minutes, I put them into random groups, and they work on the problem for another 10 minutes.
Then I show them Versions B and C and ask for their preference and reason for each version.
Version A: 18 likes, 14 dislikes
Highlighted reasons for LIKING:
It gives every detail you need to know. It tells you directly all of the information. It also seems easiest to solve.
It isn't as confusing as looking at fast-motion pictures of a circle and a square. Doing math is more exact than visual guessing. [Did he translate the animation to mean guessing?]
I am able to make my own diagram and I can try to solve an equation to find out the answer.
It is simple and not confusing. It allows me to think the way I want to and not be misled by a moving picture.
With the given information, you could construct the two shapes by working backwards.
There's enough given information to make the problem interesting and hard.
I like this one the most because you can actually read the problem and refer back to it.
I think it can be solved using an equation, and be solved more easily than B and C.
It's a more accurate way to find their areas and make them equal.
I like this version because I understand the problem.
Instead of a picture of it on paper, you have to visualize it in your head first.
You can get an exact answer. It is challenging.
Version B: 18 likes, 14 dislikes
Highlighted reasons for LIKING:
It would be cool to build the animation in GSP and solve it that way.
It's a lot more simple. It provides an image and idea of what it looks like.
I can visually see when they are equal. It will be easier to see when they are equal instead of having to do a load of math.
It is visual.
I feel I have a higher chance of answering the question with a right answer.
You can easily see when the shapes have the same area.
Version C: 15 likes, 17 dislikes
Highlighted reasons for LIKING:
It seems easier because you can just count the candies and see if they're equal.
Anyone can count how many candies there are, then subtract the extra space to get the correct area.
Some students like and dislike more than one version. My takeaway on their responses:
Version A
LIKES: (see above)
DISLIKES: Not understanding the question, or "I'm a visual learner, so I like Version B better."
Version B
LIKES: It's visual. It's easy.
DISLIKES: Too fast and hard to follow. One student, "The movement is distracting and confusing. I feel like it's too abrasive and violent. Math should be more elegant than this."
Version C
LIKES: You just count the number of candies. It's visual.
DISLIKES: Too fast to follow. It seems too easy. There's space between the candies. One student, "You can't get the exact answer... And the leftover space in one shape may be more than the leftover space in the other."
I collect all their papers before telling them which version I like. I like Version A for its simplicity. I'm curious if the stated question is enough information for them to understand. This student's reason nails it for me: "It allows me to think the way I want to and not be misled by a moving picture."
We all have students who struggle with word problems. I don't think this means we should give them fewer word problems. I think it means we should give them better word problems — ones that are written with just enough information and not embedded in contrived contexts that either confuse or insult the students. And for students who need help with the question, they get to hear an explanation from a classmate.
Version B is okay, but I don't want to start with it because I feel I'd be wasting a perfectly good question in Version A! I'd reach for a piece of string to explain this question, if needed. Version C gives me a headache.
At least one person in each group understands the question, and they do their best to make sense of it in just the short 10 minutes that we have. They're trying. And making mistakes.
Our whole-class discussion at this 8th grade level:
That "arbitrary" point P is pretty darn close to the middle of A and B. You can roughly tell from using a piece of string. Or you can tell from arriving at y2/(4pi) = x2/16 (where x is distance AP forming the square's perimeter, and y is distance PB forming the circle's circumference) — the denominators are almost the same.
Likewise, P cannot be at the center because pi doesn't reconcile nicely in the equation.
We can solve for x and y using some arbitrary distance AB, and we find y to be slightly shorter.
We can ask a related question: A circle's circumference and a square's perimeter are equal, what is the area enclosed by each? Kids can certainly think about optimization and do a little bit of calculation outside of a formal calculus class.
In addition to asking the students which versions they like, I also pose Dan's exact question to them: Which of these is a "real world" math problem? Or is none of them a real-world math problem?
Their answers vary as widely as those of math educators'. However, I find this correlation that doesn't surprise me: kids who like math more do not care if the problem is real-world or not.
This [Version C] is the most "real-world" solely because of the fact that it involves a material object which in this case is the candy. However, the thing you're solving for in this question is not very "real-world" at all. Personally, I don't care at all if a problem is "real-world" or not; I just like to solve problems.
If a problem didn't have to do with "real-world" I will still do it if I like it. It doesn't really matter.
I don't think any of these problems are "real world" math problems. I like how they make me think. But I don't think I need them in the "real world."
I wouldn't care if it is a real-world problem because I was there to learn. I think all versions can be a real-world problem because it can be needed in some situations.
I feel like all of these problems are real world... But honestly it doesn't matter at all to me. It doesn't matter if it's real world or not, it doesn't affect me wanting to solve the problem.
So, one from the kids.