My Other Math Sites
Lessons From the Classroom
Teaching Absolute Value
I know Common Core does not have absolute value in grade 8, but I'm teaching it anyway because we're still doing "algebra 1" this year. (A year ago Raymond Johnson looked into the inclusion of this topic in the different grade levels.) My 8th graders know that the absolute value of 5 is 5, and the absolute value of -5 is also 5. Some recall that it's the distance from 0 on the number line. We begin by solving a few of these: abs(x) = 4, abs(a) = 0, abs(w) = -3. A few trip up on the last one but recover quickly and move along.
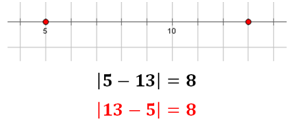
Me: What is the distance between these two points?
Class: Eight.
M: How did you get eight?
C: Subtract.
M: What about this one? The points are at -3 and 9.
C: The distance is twelve.
M: This one?
C: Thirty-two.
M: Good. Distance is always positive... How did you find the distance between the points again? What operation did you use?
C: Subtraction!
M: Then I'm going to add an equation below each number line showing subtraction. Is that okay?
M: So, the distance between 5 and 13 is 8. Then, what is the distance between 13 and 5?
C: Eight
M: Woah! It's the same? Meaning I can write the equation either way?
Kids agree that subtraction can be commutative when it's inside the absolute value bars because we’re just measuring distance. The distance from Johnny to Julie is the same distance as from Julie to Johnny. I'm not going to argue.
Me: Given two points, you can tell me the distance between them. So now I’m going to give you just one of the two points but tell you the distance between them, and you find the missing point x.
C: x is ten.
M: Yea, ten works. Let's try to read this open sentence. How would you say it?
C: x minus six... The absolute value of x minus six is four.
M: Hmmm. Oh, you say the words 'absolute value' because they're there. Let's try again without saying those words. Use the word 'distance' instead.
C: The distance of x minus six equals four.
M: Let me show you again the first one that I'd asked you. I remember just asking you, 'What is the distance between 5 and 13?' What did I not say even though it's there?
C: Minus.
M: Right. Let's not add stuff we don't need. You know naturally that finding distance implies subtraction. So, say the equation again.
C: The distance between x and six is four.
M: Or you could say...? Can we switch the points around?
C: The distance between six and some point x is four.
M: Alright. Is 10 the only answer for x? We are trying to find a point on the line that makes the equation true. So, let's use the number line to solve this. Because we know 6 is one of the points, let's locate it. We need to find the other point that would be a distance of 4 away from 6. So, it could be to the right of 6, or to the left of 6. Where does this put us at?
M: Oh, why isn't the point -6? I see a 'minus six' in the equation.
C: Remember, that minus is for subtracting. We need it there to find distance.
M: I remember. We need it.
We do a few more of these. Enough to bore us, need something new.
M: Let's try this.
C: No subtraction sign.
M: And you said we needed it. Then create it. Make it happen without changing the problem of course.
C: Change it to minus minus...
M: What does this problem say now?
C: The distance between x and negative eight equals five.
We do a few more of these. Enough to bore us, need something new again.
M: What about this?
M: Nothing terribly exciting. The other point(s) that we find is now worth 2x, so we just need to solve for x.
Then we do a batch of these:
Hey, what about these, where there's more stuff stuck around the absolute value quantity. Oh, we just need to first isolate the absolute value, then it's business as usual.
We spend the next whole class using Desmos to explore the shifts/changes to the parent absolute value function. Students need to write down their predictions first before graphing. One student was very excited when she got the V-shape to turn upside down.We discuss some real-life scenarios that may involve absolute values: margins of error, ranges of measurements: distances, scores, speed, temperatures, pH levels, elevations, etc.
Not proud to admit that I spent a lot of hours in college playing pool instead of studying, but never once did I associate the path of the ball as an absolute value function. Consider me odd if I always thought of angles instead.
Solving absolute value inequalities start similarly enough. Kids know from graphing inequalities that there's "shading" involved. They also know the difference between open and closed points. So I just have the kids use their thumb and forefinger to indicate the distance between the two points, then if the inequality says less than [or equal to], then it's natural to pinch their fingers closer together, indicating that the region inside the points need to be shaded.
The textbook will tell kids to set up the "two cases" to solve these inequalities (same thing with equations).
Then, kids are asked to graph the solution. But if kids learned to solve using the number line itself, then there would be nothing to memorize because they learned distance way back when they started learning to crawl. And since the graph shows the solution, then writing what that solution is is easy because it matches the graph. Like below, x lives on the green line between -8 and -2, being ≥ -8 and ≤ -2.
For greater than inequalities, the student would naturally spread his fingers apart to indicate shading outside of the points.
I don't know why there seems to be a lot of rules when learning to solve absolute value equations — which inequality sign for when it's and or when it's or.
Classroom Management
Give or take, scenes from my classroom last week:
A walks into class, talking at full volume until someone shushes her and points to the obvious math talk on the board.
B slouches in his desk, head barely above seat-back.
C decides to dump out contents of his binder to find the math paper from 24 hours ago.
D talks while I’m talking.
E and F are talking while someone else is sharing.
G and H are playing footsie; H is better at this.
Someone lets out a shockingly loud fart — we all look at row 7, seat 5 because the occupant is giggling and beaming proudly.
I continually scans the room like she’s seeing it for the first time.
J asks to use the restroom when there are fewer than ten minutes left of class.
K and L try to talk to each other half way across the room.
M makes squishy noises with his water bottle.
N taps his pencil.
O clicks his pen.
P and Q… well, they’re just minding themselves.
R blurts out, “I already got the answer!”
S needs to borrow a pencil from classmate for the 95th day of school.
T volunteers, “Yes, I’m very bright. I’m a genius. But I need help with section nine four.”
U returns my look with a look of what-Mrs.Win-?-I’m-doing-my-work-see-?-hehe-okay-I’ll-do-my-work-now.
V yells at person sitting in front of her, “Stop pushing your desk into me!!”
W walks across room to get a drink of water. Five sets of eyes follow W and then at me to see my reaction.
X asks out of the blue, “Have you eaten at that Korean place, Mrs. Win? It’s so good.”
Y sticks out his foot to trip Z as he walks by.
A through N immediately engage in lively conversations just as I say, “I need you to take out a piece of graph paper.” So, I have to say, “Guys! You don’t have to talk just to get out a piece of paper!”
O through Z immediately engage in lively conversations just as I say, “Make sure your name is on the paper.”
I may only talk about classroom management with your understanding that my own classroom is sometimes chaotic, sometimes louder than it should be, sometimes messy — but somewhere in this soup of chaos, noise, and mess, I have to believe that there is learning of mathematics. More so on some days.
I can’t help but draw parallels between teaching and parenting because both roles have defined me. Their enormous responsibilities have brought out the best and worst in me. It’s easy to love children. It’s much harder to discipline them. A wise colleague once reminded our staff that discipline is not a dirty word — to discipline means to teach. And I think teaching is the purest form of love because teaching is sharing.
Classroom management is used interchangeably as classroom discipline, and that’s okay. It’s all part of classroom teaching. I’ve been around long enough to see teachers leave the profession because they lacked “classroom control.” Nothing in teacher school adequately prepares you for this. No manual outlines what to do when a kid cusses you out. Step 1: remain calm. Step 2: breathe deeply and count to 10. Step 3: fuck this shit and find another job.
I bought this hardcover book long ago.
I’m sure it’s full of good intentions and sound advice. (Serendipitous that 20 years later the author Randall S. Sprick enters my life again when our school currently adopts his CHAMPS program.) But it’s really hard to see classroom management in action from reading a book or a blog post. It’s ideal to directly observe a teacher and her students, and not just for a day or two, but over a period of time. The classroom culture is undeniably real and one has to be in it to fully appreciate and honor this culture. I know there’s a thing called student teaching where one is immersed in a real classroom for a semester. But I swear to God, the kids we get during student teaching are sent down from Heaven. And the real kids, the ones we get after we’re hired and on our own, are sent up from the Other Place.
What I’m saying is it might be very helpful to observe these same kids whom you currently have in another teacher’s classroom.
It was around the end of the first quarter of my third year in the classroom when a colleague — a new hire — told me the vice-principal had suggested for her to observe me for a couple of periods. Afterward, she said, “Fawn, Joey is like a different kid in your room. I never knew he could sit still for 5 minutes! He’s out of control in my room. In your room, he just… blends in.”
Apparently Joey behaved differently for different teachers or at least in different settings. The teacher didn’t come back the next year — and this made me sad because she worked hard and wanted to be a teacher. There were other teachers who left the school after putting in just one year. It was a “tough” school — plagued with the usual inner city inadequacies and brokenness.
Having said that, I find kids are kids. I’ve taught in the poorest neighborhood and in the most affluent. Kids who live in fancy homes have better rides to school and wear designer labels, but at their core, they are kids who mostly want to learn and not be shunned at the lunch table.
We can’t say we possess great classroom management skills if we could pick and choose where and whom to teach. There’s a quote out there that I like: Parents are sending us their best; they’re not keeping the good ones at home. So, if we took the students out of the classroom-management-success equation, we are left with two variables: the teacher and the classroom.
The Teacher
LOVE the kids. Fine, we don’t have to love all of them because inevitably each year there’s always one (or two or three) who pushes all our buttons and makes us throw wild tantrums at home. But aren’t we supposed to be tougher than the toughest kids? How is this child’s home life? And is this child behaving like this in all her classes? There’s something to be said about killing ’em with kindness. Why are we in teaching if we didn’t love children and love helping them learn?
Show students respect. It should be the other way around — that kids must automatically respect us for our age and our college degree. But whom are we kidding. We all know of a few adults with advanced degrees who need to stay the hell away from us because they’re mean and psychotic. Kids tend to misbehave more for teachers whom they don’t respect. Do we honor their struggles and offer to help? Do we show up at their games and show genuine interest in something they do outside of school? Do we say please, thank you, and sorry each and every time that warrants it? Do we spend time outside of class to help a kid like we said we would?
Command respect. Respect has to be mutual. Like trust. We have a great opportunity to be a role model for many kids. We can’t command respect by being “pals” with the students. We all know of parents who try to be buddies with their kids. We should never ignore a disrespectful comment/tone/gesture from a student. Because if we do ignore it, it won’t be the last time it happens. How do we speak of our colleagues and administrators to students? How do we speak of our family to students? Are we consistent and honest with them? Do we follow through with consequences?
Have a sense of humor. When was the last time we laughed with the kids? The lighter moments make us more approachable and compassionate. When was the last time we shared a bonehead mistake we made? Who makes us laugh? Humor allows us more room to breathe when we need to get tough with a kid.
The Classroom
Have good lessons. I can almost tie every misbehavior or off-task behavior to the lesson itself. A good lesson is no good until it’s delivered well. Logistics. A content-rich lesson that doesn’t take into account student movement and/or material management is asking for all sorts of mayhem. Please don’t envision a “good” lesson only as a hands-on task that involves group work. A good “lecture” — aka direct instruction (maybe) — should capture students’ attention too if we drew them in with questions and invited them to make conjectures along the way. Good story telling [that relates to the math topic] will have their eyes wide open and ears perked up. Good lectures are awesome.
Establish routines:
One of the best things we have established school-wide (K-8) from the CHAMPS program is a hand signal for silence. What’s your signal? And we need to wait for that complete silence before we speak.
Kids will forget some of the routines and look at us like we’re crazy when we remind them. So, remind them and don’t look so crazy, like don’t make a big deal out of it.
We need to remember that kids [and adults] crave structure. We are creatures of habit. A good structure does not mean it has to be fixed; it means it’s flexible. Like a building that’s earthquake hearty.
Noise level. What is our tolerance level? Dead quiet has to mean dead quiet. Whispering is not dead quiet. What’s the appropriate noise level for small-group work? How often do we find ourselves yelling? There’s no rule that says we can’t stop the activity — especially when it comes to safety — if kids aren’t following protocol.
The ONE thing. Do our kids know the one thing that upsets us? My one thing is I hate mean people. So I get really, really upset when I see a kid doing something mean to another. The lesson stops. Everything stops because this is a big deal. Most of them will say that they were just playing around. We talk about that — playing and inadvertently hurting someone. Our classroom needs to be a safe place. And I want this to be a money-back guarantee with kids; it’s my one thing.
I’d taught at my first school for 8 years before I interviewed with another school. Near the end of that interview:
Vice-Principal: Fawn, there was one thing in particular that your former vice-principal had shared about you that stuck with me.
Me: Yeah?
VP: He said, She was the only teacher who could get our eighth graders to walk perfectly in a straight line and quietly from her room to the gym. How did you do that?
M: I just asked them to.
VP: You just asked them?
M: I mean they know what quiet means and what a straight line is. I told them that we needed to show respect to the other teachers and their students when we pass by their classrooms. We show this respect by walking quietly and orderly so we don’t disrupt them.
VP: How long did it take to get them to do that?
M: First time. Well, we simply didn’t move unless they were quiet and lined up. I saw pride in them as they walked. At least one teacher would happen to watch them go by and complimented them. When we got back to our room, I always thanked them and told them they made me proud.
Barbie Bungee Revisited and Better Than Yours Class Lists
This year I've taken away a lot of my step-by-step instructions for the Barbie Bungee activity that I'd posted 1.5 years ago. They get no handouts, only some verbal instructions:
[Pointing to the ceiling] See that gob of tape up there? That's leftover tape from previous years where Barbie had taken her jump. It should be at 3 meters up. Well, a small ruler will come out perpendicular (somehow) to that pole where the tape is, and that's Barbie's jumping platform. The ruler is like her diving board.
The goal is to give her the most thrilling jump — her head dips as close to the ground as possible without actually touching it. Yes, her hair hitting the ground is fine. Her jump line is made of rubber bands tied together with slip knots. (Why must we use brand new rubber bands?) You'll work in groups of three, says Instant Classroom.
So, aside from the Barbie doll, what do you think your supplies will be?
Rubber bands! How many? Lots! A hundred!
Try six. Actually seven, but one must be completely wrapped around her ankle, like this.
With only 6 rubber bands, your job is to figure out how many more rubber bands she'll need for the most thrilling jump from 3 meters.
Can we weigh her?
This is like the Vroom car!
So we have to graph, then do the extension thingy. Extrapolate. Oh, the equation is in slope-intercept form!
(We've been looking at word problems and writing linear equations that would be more appropriate in standard form or in slope-intercept form.)
Your team will have until the end of tomorrow's class time to submit your number of additional rubber bands you'd want.
For easier management of the rubber bands, I get them ready in bundles of 7, one to each group for testing and data gathering, and in bundles of 10 and extras to give out as requested on jump day.
I liked the messiness of their initial work. (I didn't give a handout or many instructions for Vroom! either, and they did fine.) Kids doing whatever they think they should do, measuring incorrectly, plotting ill-looking graphs, talking and criticizing one another. I was debating when I should intervene, but it was good for me to just observe and listen in.I waited until the next day to point out stuff. Actually I never told them what they should do, I tried instead to ask them how something should be done. I don't think one single idea came from me — someone always had the answer I was hoping for, so all the "correct" ways to do things came from them. My phone apparently didn't have enough memory after this one clip. It was fun. (One kid also brought up that this was like the Stacking Cups lesson that we did.)
This might seem to you a DUH! share, but I only thought of it earlier this year, and I feel like I invented the paper clip. We all have class lists, of course. But is each of your class lists on a strip of paper like this? And in different colors? I didn't think so.
I have semi-thick stacks of these to use for just about everything. What a pain to write down kids' names for this and that. Instead I just pull out a strip and highlight so-and-so's name and note the reason.
I staple one set of strips together, put a date on it, and kids pass it around to each other to sign in for after-school help — they just need to put their initials next to their names.
Those who need to come in at lunch recess get their names highlighted on the strip.
I use it as a hall pass when I need to send 2 to 3 students at a time to the library.
I highlight a kid's name whose parent I need to contact, then use the back of the strip to make notes from our conversation.
It's a great tally sheet for whatever during class.
Endless uses.
Hotel Snap
[NCTM Illuminations has my blessings and thanks to re-write and feature this lesson on their site.]
Andrew Stadel and I recently presented this task at the 2013 CMC's North and South Conferences.
The Challenge
As a team, build a hotel that yields the highest profit [score].
Rules and guidelines for building the hotel
Each cube represents a hotel room. All 50 cubes must be used.
Hotel must stand freely on at least one side of cube. Here’s a non-example because it’s tilted.
Entire hotel is one piece. A non-example due to yellow cube not attached:
All rooms must have at least one window, a window is any exposed vertical side of cube. The white cube below has no window.
Building costs and tax (daily rate)
Land costs $400 per square unit.
Land refers to outline of top view of building.
All enclosed land is charged, for example, squares marked 8, 9, 10, and 11 in the left outline are open space, but because there's no access to the outside, you are charged for these 4 square units.
A roof costs $10 each, roof is any exposed top side of cube.
A window costs $5 each.
Tax on height of building is calculated by multiplying the tax rate for the highest floor by the total land cost.
Floors 1-10 —> 50%
Floors 11-20 —> 1000%
Floors 21-30 —> 2000%
Floors 31-40 —> 3000%
Floors 41-50 —> 5000%
Income from each type of room (daily rate)
The more windows, the more income.
4 windows, 1 roof = $600
4 windows, 0 roof = $500
3 windows, 1 roof = $300
3 windows, 0 roof = $250
2 windows, 1 roof = $200
2 windows, 0 roof = $175
1 window, 1 roof = $150
1 window, 0 roof = $125
Scoring
Your net profit/loss income will be checked for accuracy. A deduction of 50% of your error will be applied to the actual number. For example, your building nets a profit of $13,500, but your group submits a profit of $15,000, therefore you're off by $1,500. Then 50% of this error ($750) will be deducted from the $13,500 to give your team a score of $12,750.
If your calculations are right on, then your team's score will be awarded an extra $1,000.
Adapting this lesson
Change the number of cubes, as few as 10-15 cubes for younger kids, and maybe up to 100 cubes for high school students.
Also for younger kids, have the Excel file (more on this later) readily available on computers so kids can go back and forth between checking their profit margin and tweaking their hotel rooms — so no calculations needed on their part, they just need to be able to know how to count the different types of rooms.
Older students can create the spreadsheet, it's great practice for understanding how cells work and formulating equations.
Adjust the time for individual and group work based on your expectations.
Modify, take away, or add to the rules and guidelines.
Change any of the costs/income/tax numbers.
Change how you reward accuracy or penalize mistakes.
Ask each group to estimate and rank the profit margins of other teams' hotels just by looking at them (like on a -5 to +5 scale, -5 for biggest loss and +5 for biggest profit).
Ask, "What if all costs and tax stay the same, but now the incomes for the rooms are all reversed so that 4-window-1-roof earns only $125 while 1-window-0-roof earns $600? How would you build your hotel using the same rules?"
If I were to do this with my 6th graders, I'd first have everyone build the same 10-cube hotel with me, then we'd use this hotel to familiarize ourselves with the different types of rooms and tally them up. We could calculate the costs and income together for practice.
How I ran the lesson with 8th graders
(I did this lesson with two classes of 8th graders, one geometry and one algebra. We have 57-minute periods. This lesson took 2.5 periods. I'm so scripted here because the one thing that kids wished they had more of was time. Your teacher instruction needs to be tight and supplies distribution needs to be efficient to allow for all the student work time needed.)
State the challenge of task.
State the rules/guidelines.
Give each student a zip bag with 50 cubes — but I first took time to show them that how they see the cubes now is how they need to be put away when we clean up.
Give each student this cost_income_sheet:
Set timer for 15 minutes for individual work, reminding students that later they will be randomly assigned into groups of 3 to work on one hotel.
While students are working, I use Instant Classroom to put kids into groups of 3.
When the timer goes off, I give the following instructions:
I now need you to listen to directions for working with your teammates, and when I'm done giving these instructions, I will set the timer for 25 minutes for you to work. During this time, you'll need to do the following:
Share and discuss the best model to represent your team's hotel.
You may modify this chosen hotel, or you can even start from scratch, but watch your time.
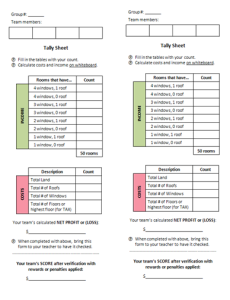
Use this tally_sheet to record your room counts, land, roofs, etc. — remember this is just a tally sheet, so you want to do all your calculations on whiteboard.
On the large whiteboard, divide it into 4 quadrants, and your group will need to fill in 3 of the 4 quadrants answering these questions. Watch your time carefully because when the timer goes off, the hotel you have in front of you is the one you must keep as is.
Allow a couple of minutes for groups to get supplies and settle down together with their individual hotel models. One tally sheet needs to be passed out to each group.
Timer is set for 25 minutes. Monitor the groups, check for understanding, and listen in for building strategies. Keep counting down the time every 5 minutes.
When timer goes off, ask groups to break down the hotels that were not selected and put the cubes neatly back into the zip bags and return to the front.
Next day...
Kids get back into their groups with their whiteboard and hotel. Some groups may still need to finish filling in their tally sheets and whiteboards.
The question for the 4th quadrant is now asked: "If you could relocate just 5 cubes on your hotel, where would you place them?" Remember that you are no longer allowed to change your hotel, this question is just a what-if scenario.
Allow 10 minutes for groups to finish filling in their tally sheets and answer all 4 questions on whiteboard.
As indicated on bottom of tally sheet, groups are asked to bring up the tally sheets to teacher to check their calculations and arrive at the final score.
The Excel sheet
I have two files: one locked and one unlocked. The "locked" one so of course no one can inadvertently change the cells, especially wise if you give kids access to the file to use on their own - only the blue cells to enter data are open. The "unlocked" file is so you can edit as you please.
Notice that all the cells appear in the same order as the tally sheet, makes for quick entries with instant results. My husband gets most of the credit for this, I still claim credit for making it simpler.
Math Practices
I found this form 8_MP_questions_to_ask online and can't find it again to cite the source.
I'm making good use of this form after almost every task now. Students do this for homework. I ask them to highlight the questions that came up during the activity - from teacher, peers, and self.
We discuss this as a whole class the next day and generally come to a consensus of which math practices our task had fostered.
Reflections
We presented this lesson because it went really well in the classroom. The kids were completely engaged. They collaborated, talked a lot among themselves about what they were building and thinking, but they were pretty much dead silent during the initial individual work time. I love seeing the structural varieties — this was true too among the hotels built by math teachers.
To not spoil the fun, I won't post pictures of the high-profit hotels here, but I'd love to learn what some of your profit numbers are from your class.
Vroom Vroom
I normally share a lesson that I've already done with students, but I'm still tweaking this one and needing to write some thoughts down before my noggin turns back into soft tofu. I bought these 14 pull-back friction toy cars (2 sets) for $30 at Costco. Amazon posts a video of how well these soft squeezable cars can stand up to toddler abuse.
On your mark...
Each team of 3 students gets 1 car.
How far the car moves forward depends on how far it gets pulled back — good lesson too for talking about potential and kinetic energy.
The challenge is to get your team's car to go a certain distance (reach finish line) without going over. This distance is not revealed until later.
To predict for how much pull-back a car needs to go a certain distance, students "test drive" their cars for pull-backs of 2, 4, 6, and 8 inches.
Get set...
Students are instructed to take measurements from the car's front wheels.
The blue tape marks the starting line. Front wheels line up at the front of the tape.
The car is then pulled back a certain distance — here it's 2 inches — and let go.
When the car stops, the distance traveled is measured from front of wheels to front of blue tape. Looks about 13.2 inches here.
Go!
Teams do 3 trial runs.
Record and graph data on Desmos.
Now teacher reveals and marks the distance each car needs to travel without going over. Say 15 inches.
From graph, students extrapolate what the pull-back distance would need to be for car to move forward 15 inches. This distance is recorded and cannot be changed.
Teams line up with their cars — one at a time — to pull back and let go!
Winning car is one that reaches closest to finish line without front wheels going past it.
Considerations
The cars roll best on bare floors. My classroom is carpeted, so we'll need to do this outside.
It's fun that the cars actually vary in speed for same pull-back distance. The sports car (bottom left in above picture) is fastest.
My kitchen floor is not big enough to test longer than 8-inch pull-backs, but the graph appears more parabolic.
The data looks pretty awful, doesn't it? Kinda? Maybe?
Ginny from Mathalicious was in the kitchen when I was playing with these toy cars. She shook her head and wondered if empty nest syndrome got the best of me. No matter. I think this will be a lot of fun. Will report back and post some pics.
[Updated 12/01/13] Jon Orr did this lesson with his Grade 9 students and wrote a great summary on his blog.
Here are a few pics from my class:
And a couple of video clips:
Deconstructing a Lesson Activity – Part 2
Previously: Deconstructing a Lesson Activity - Part 1
No matter what I write in this Part 2, I hope it's not a wrap-up of this topic. On the contrary, I hope it opens up and extends our conversations on improving the implementation of rich tasks in our classrooms.
Physical arrangements, whiteboards, groupings. The student desks are set up in rows and columns in my classroom. Not terribly exciting, but don't judge a teacher by his/her furniture arrangement. When I'm given 38 desks (I had 37 students in Math 6 last year) and x square units of floor space, my creativity is stifled.
Work with whatever space you have. Push the desks together, pull them apart. Kids don't mind sitting on the floor. (If they do, ask them to stand and see if they like that better.) Can they work in the hallway — or outside if you're in warmer climate — where you can see them from inside the room? Just make sure you are constantly roaming among the groups.
Big-ass whiteboards. Nathan just wrote a letter asking for these. Last summer I sent my principal the link to Frank Noschese's post — and the whiteboards were waiting for me when school started. I got ten 2' × 2.6' boards, each at $10.50 from here. Please get them. By far the single best school purchase, worth their weight in gold. Just how much do I love these? You touch my whiteboards, I'll kill you.
Randomly assign kids to groups. We do group activities often enough that eventually pretty much every kid ends up with somebody new in the group. If you try to group them "heterogeneously" with high-medium-low kids, then you accomplished just that — you just told them who's high, who's medium, and who's low without saying a single word. Kids aren't stupid. I use Instant Classroom to randomly assign. You can always use your discretion to change a few kids around after the computer picks them — but still let the kids think that the computer did all the choosing. I never heard any whining. Kids don't whine at what the computer says.
Group roles. What are these?? (No, I'm asking you!) Like "facilitator," "recorder," "reporter," "budget person," "dietitian," "hairdresser," etc... These roles wouldn't work with problem-solving tasks. I don't want a kid sitting there doing nothing because it's not time for his role to occur yet. Please, no assigned roles. Except the one about trying to solve the problem.
Grading this type of task. I don't see dead people, but I hear student voices all the time. While I enjoy grading as much as I enjoy poking needles in my eyes, I hold certain beliefs about grading problem-solving group tasks (and the student voices that guide mess with me). And my possible reasons/solutions for them?
It is wrong to give a lower grade because they socialized too much instead of focusing on the problem. (We're teenagers and you expect us not to socialize? OMG! Did she just put me and Joey in the same group? He's sooooo cute. How's my hair? This problem is just too hard anyway! We really tried but we got stuck and you were too busy with another group to help us. Laura is such a show-off. I wish Andrew would grow up.) If the whole group is off task, then I'd seriously reconsider the relevance/engagement level of the task and the social dynamics of the group. It's back to that Step 0 of picking the right task that's engaging and has low entries so everyone can get on board. It's my fault that the kids are not on task.
It is wrong to give a lower grade because they did not come up with the correct solution when the bell rang. (Sucks that we didn't win the game today, but we still had a good game, right? Didn't we work well together as a team, especially on defense? Nice block there, Mitch. I almost had a pick right there if my damn leg didn't cram up! Ha, now I know what Coach meant by the hook-and-lateral play!) Our goal of wanting kids to engage in problem solving is to honor the process that they go through — their thinking, their collaborating, their critiquing one another. We want to tap kids' two most abundant natural resources: their curiosity and their need to socialize. I simply cannot justify putting a grade on this.
But bottom line, you grade it if you want to. Don't grade it if you don't want to. I graded fewer than 50% of the tasks that were done in class last year. When I did "grade" them, I gave full credit. To worry about how to grade group tasks is really to sweat the small stuff. That said, if you had a handout for each student that went with the task, then it's fair to give the individual grades.
Establishing a classroom culture of problem solving and finding time to do so. Stephanie Reilly's question in Part 1 helps me shape what I'm trying to convey in this section.
I can't think of a better day to start doing problem solving with kids than Day 1 of school. Kids pick up on what we say we value and what we do to back that up. Set a goal to do one task every two weeks. Too ambitious? Then once a month. Just please don't give up. On Day 1, I might just start with Pyramid of Pennies (Ha! I nailed the spelling there) or the new Bracelet Craze problem. If I were a student and knew that all my teachers would go over "Rules & Procedures" on the first day of school, then I'd be tempted to feign high fever and induce vomit to stay home.
However, you need to come up with guidelines for group work that you will share with kids before they begin. Culture takes time. It takes a lot of reminders too. I'll share what I say [for guidelines] to the kids under "group time" in the last section of this post about implementation.
Post the strategies for problem solving in your classroom. I have these on just regular size paper, but laminated, and we refer to them all the time. You know, strategies like these ones.
Teacher concern: I'm afraid I don't have time to do this because there's still so much to cover in the textbook. You can't do this and feel guilty. (Remember how crazy in love you are supposed to be with the tasks you choose for them?) You have to be okay with not being able to go cover the textbook front to back. The person who tells you that you have to do so is delusional and mean. Common Core does have fewer domains and standards at each grade level. Spend this summer mapping out key concepts and lessons. I believe in having some sort of pacing guide, but I don't believe in having it dictate how we move through the year — the kids and your formative assessments of their learning should govern the flow. I haven't done research or have hard data of my own to give you, but I believe your kids will do better on year-end assessments if they have been exposed to problem solving throughout the year. Trust me? :)
Carve out time by re-examining and possibly eliminating things that you normally do.(For the last two years our students had two periods of math each day. I think this is going away next year, so I have to re-think this through too.) Besides just having better classroom management — meaning it's not taking you 10 minutes to get the kids to settle down and start class — how effective is your use of class time when you do these items?
Warm-ups
Games
Review games before a test
Pre- and post-surveys
Benchmark tests (beginning, mid-year, end-of-year)
Stuff that kids can do at home blindfolded (I think we know what these are.)
Class parties (What the hell are these? I like parties too, but let's have them at lunch time.)
Lastly, please don't forget that these are perfectly good SCHOOL days for doing mathematics: First day of school, last day of school, last day of the quarter, first day of the quarter, whatever day. The day before Christmas or spring break. The first day back from an extended vacation. Sub days. Your sub is perfectly capable of passing out a meaningful handout (it's meaningful because you made/selected it), and it will go well because you have already pre-taught the kids what's on that handout — give them a sneak peek at it! — and shared with them your expectations the day before you leave. If there's one assignment worth grading, then it's the work that they do while your sub is there.
Finally, implementing the task. Thus far I've covered the behind-the-scenes stuff that was missing from my lesson posts. The task itself is actually a lot more straightforward — pretty much what you read on my lesson posts is my best storytelling of what went on in the classroom.If you're doing an actual 3-Act lesson a la Dan Meyer, then you're good to go! These are some of my favorite 3-Acts that I'd written up:
File Cabinet
Taco Cart
Equilateral Triangles
Penny Pyramid
So, this is an outline of how I implement a non 3-Act problem-solving task.
Ask for a volunteer to read the problem aloud (5 minutes). Each kid gets a copy of the problem to follow along. After it's read aloud, everyone reads the problem again quietly to self. Then my questions begin for the whole class:
What are we trying to solve for in this problem?
What information do we know?
Is there information that you wished you knew? Why is it not given then?
What's the first strategy you have in mind that might help you attack this problem? And why did you say 'do a simpler problem'?
Depending on the task, I've also begun to ask — instead of the questions above — these two questions from Annie Fetter (YES! Please watch the 5-minute video if you haven't.) The kids write down their answers, and I randomly call on them to share.
What do you notice?
What do you wonder?
Quiet individual work time (10 minutes). You have to allow for some individual thinking time. I can't work on a problem when others around me are talking. So I set a timer for 10 minutes. Of course it doesn't have to be 10 minutes, it's up to you and depends on the problem, but this is NOT the amount of time in which I expect any kid to solve the problem. If a kid does solve it quickly, then hopefully you have an extension — you should always have an extension — ready for this kid. If a bunch of kids could solve it quickly, then you've chosen the wrong task, too easy. Back to Step 0.
I say something like, "I'm setting the timer for 10 minutes so you can think about and start the problem on your own. There's no talking and no sharing at this time. You'll get in groups to continue to work on the problem after the quiet time. You're welcome to get up without my permission to get any tools (protractor, compass, ruler, graph paper) that you need. Do you have any questions for me before you begin? Remember our rule of NEVER TELL AN ANSWER. Go!"
While they're working, I use Instant Classroom to form the groups and move some kids around if necessary.
Group time (30 minutes). Again, this is a very generic time allowance. You're the teacher, you'll know by how much to shorten or lengthen the time depending on the groups' progress or lack thereof.
I say something like, "You will now continue to work on this with your group mates. You will use the large whiteboards to show your work. Everyone has his or her own marker to use. But now I'll explain more by what I mean by 'never tell an answer.' If you think you have an answer already from working on it just now by yourself, then please don't share it with your group. Choose to be the last person in your group to speak because I actually need to speak with you first.[1]
... Also, every time we do a task and I hope we get to do lots of them, I ask the computer to randomly assign you in groups, so if you have a complaint, take it up with the computer. If your group would like more individual work time, like 5 more minutes, then that's great and fine by me....
I'm interested in your working together to solve this task. I'm not asking you to become best friends. One person speaks, everyone else listens. Argue about it, but be respectful. Ask questions of one another. Don't take so-and-so's word for it, ask him or her to explain it. Don't let others think for you. Help each other out. Maybe this whole structure is new to you, don't worry about it. I'll walk around and listen in and smack you in the back of the head when you don't quite have it right. Just kidding. Not. Yeah, I'm kidding. Go!"
I actually repeat much of this same spiel throughout the year.
[1] So I talk privately to the student who does have the correct solution and suggest a few things:
Can you solve the problem a different way? (It's important that you do not force a student to find another strategy especially when you can see that she has found the most elegant one already — this just seems counterproductive to me.)
I'd like you to try the extension to this problem. What if...?
I need you to go back to your group and practice really good listening skills. I just want you to listen to your teammates talk. Then see if you can help them by asking questions only. Kinda like what I normally do with the whole class. You may give them one hint if they're really stuck. You want to give that a try?
Teacher role during this group time. This is where the book 5 Practices comes in for me. I've been presenting its contents at workshops over the last two years. There's no way I can do it justice here, and I've already written a brief post on it just as a quick review.
The gist of it is that I go around and listen in and check on the groups' progress. I ask questions of specific individuals in the group.
Hey, Julia, can you explain to me what I'm seeing here on the whiteboard? Maybe you didn't write it, but whoever wrote it, did he/she explain it to you?
Jonathan, I'm not sure where this equation/number comes from. Please explain.
I saw this same strategy at Erika's group. Allie, did you come up with this strategy? If not, what is yours? Where is your understanding of the problem so far?
Joey, what has Cindy contributed to the group thus far? (If Joey says, "Nothing," then I'll ask Joey again, "What have you contributed?" I don't remember ever having two people in one group who have not shared anything. Remember they had 10 minutes of quiet time to work on this already. They have something to share!)
Cole, your group is over here. I don't want to tell you that again. (And I never have to.)
Now, when there's one group that has made a lot more progress than the other groups, I ask for the whole class attention and say, "Julia's group has made an important connection, so I'm going to ask someone from her group to share with the class one hint, one strategy, or one something that would help all the groups along. Listen carefully."
If none of the groups has made progress, then the teacher needs to jump in with a hint. But be patient too!! You have to watch the clock. How much time is reasonable? Are the kids mostly working and asking questions of one another? If they're exhibiting productive struggle, then let them be. Nobody is going to die if you extend this lesson another day.
The SHORT version can end here after the groups have figured out the solution. Maybe not all the groups finished, but remember, most of them did. Depending on the task, depending on the students, depending on time, depending on whatever you deem as important, you can end the lesson here and not feel guilty that there was no large-group sharing at the end, no connections made among the different strategies. Instead, focus on all the mathematics that you did allow the kids to be engaged in. I see enough teachers feel discouraged that they "didn't get to do everything that I wanted to do" — it's not about doing everything, it's about doing something to get started, to get better, to suck less each day, to remember why you went into teaching in the first place.
The FULL version includes the "connecting" piece that the 5 Practices refers to. It's about making connections between the different strategies, and you accomplish this by having the groups share their work on the whiteboards. (This step is moot if the task didn't have more than one strategy.) Kelly O'Shea is my whiteboarding goddess. And connecting is also about you the teacher making the connections of all their work back to the original intended learning goal of the task.
Who says you can't add the connecting piece to your short version 2 or 3 days from now (hell, even two weeks later) and make it a complete kick-ass full version? In real life we return to problems all the time. Snap a photo of each whiteboard if the kids need to refer back to their work at a later date but you have to use the whiteboards for another class in the next period. Problem solved.
You can do this. We can do this together.
Deconstructing a Lesson Activity - Part 1
[I've decided to break this post into two parts because I don't want to bore and/or discourage you, and I need to take a breather. These two posts in particular are truly my labor of love because if there's one thing that I find myself proficient at implementing in the classroom it is problem solving. I hope you'll find some parts useful.
I've done a fair share of posting actual lessons and pictures from my classroom in this space and on my 180 blog [that's no longer available, sorry]. But I'm afraid they appear polished and therefore unhelpful to teachers who are trying to implement problem solving, white-boarding, 3-Act lessons, or any task-oriented activity in their classrooms.
So here's my earnest attempt to deconstruct the structure of a lesson, get down to the nitty-gritty, take small bites (and spit out what you don't like), and make it real because if it ain't real to you, then it ain't gonna happen for your kids.
Some important prerequisites. I need you to have this mindset or else we're not going to accomplish anything.
You care that kids learn something meaningful in the 45-minute period that they are with you. You might be thinking, Of course I care or else I wouldn't be teaching. No, I don't mean that. I mean the "something meaningful" part. What did you intend for your kids to learn today?
You might very well fail at implementing a 3-Act in your first attempt. And fail again and again. But you can't give up. You can't give up because the kids need you to persevere, it's the same MP1 that you ask of them. Cry and bitch about it at home. Adopt a puppy if you live alone. Eat ice cream. Drink a beverage with higher alcohol content if you need to. Get a punching bag or go to the gym.
You need to be okay with leaving some children behind on some days. I'm not a miracle worker. Neither are you. One hundred percent student engagement 100% of the time is a myth sold by the snakes-oil salesman. You can't differentiate every lesson. You can't reach and motivate every child. But you will reach and motivate the ones that you can. You'll die trying because you love these kids, but you're going to realistic about it.
Surround yourself with helpful colleagues. They listen and are willing to observe your class and give critical feedback. They remind you to eat. They eat lunch with you. They don't badmouth kids when their lips are moving. They believe Happy Hour is invented for schoolteachers and feel it's sacrilegious if they went without you. The toxic people in your life can just piss off. If no one is around and you really need to vent, please email me at fawnpnguyen at gmail dot com. I am a much better listener than I am a writer.
Piece de resistance. I carry out the lessons through the lens and language of these bodies of work. It's okay if you don't have the 4 books, but I highly recommend them if your school or personal budget allows.
5 Practices For Orchestrating Productive Mathematics Discussions by Margaret S. Smith and Mary Kay Stein
Thinking Mathematically by John Mason with Leone Burton and Kaye Stacey
Mindset: The New Psychology of Success by Carol S. Dweck, Ph.D.
12-minute video of Dan Meyer's TED Talk: Math class needs a makeover
Improving learning in mathematics: challenges and strategies (PDF file) by Malcolm Swan
The Art of Problem Posing by Stephen I. Brown and Marion I. Walter (I just borrowed this book from UCSB last week. It's wonderful. Nat Banting reviewed it here.)
Picking the right task. Think of this as Step 0 of the 5 Practices. If I picked the wrong task, then no sound pedagogy or fancy technology would be able to save me. I'm done. Lesson sucks. Game over. That's how important this step is. What is a "right" task?
It's age appropriate. I don't mean for you to go searching under tabs that read "6th grade" or "algebra 1" either. What's age appropriate for your 6th graders might be too high for my 6th graders. Know your kids. An inherently good task would cover a wider range of consumers. If it's early in the school year and you don't know your kids well enough yet, then choose a higher level. It's a crime to underestimate children's mathematical abilities. Dan Meyer speaks volumes about "low-entry high-exit" tasks and Ladder of Abstraction.
It has multiple strategies. At least 2 ways of solving. Single-strategy tasks are like culs-de-sac. There's nothing to do except to turn around. Think how fruitless and boring it would be if you asked kids to share their different strategies and there wasn't one to begin with. Also, just because you'd struggled with a task does not necessarily mean all your kids will. Maybe there was a more elegant solution that you did not see. Be humble, ask another colleague or throw it out on Twitter for others to give it a try. (Please tell me you have a Twitter account. Mine is @fawnpnguyen.) And if your gut thinks there's another way to solve a problem, then be honest with the kids and say exactly that. They'd be thrilled to death to learn that they'd helped you see something differently. My favorite moments for sure.
You are crazy about the task. I can't speak for what tasks/problems turn you on, but I know what my favorites are. (And every.single.time we do a new task, I half-jokingly say to my students, "This one is my absolute favorite!" The kids roll their eyes at me, but they know I'm passionate about it.) It's hard to get kids to like things that we ourselves do not care much for. That's kinda fraudulent. I'm be a big fat liar if I say that I like all the tasks Andrew and Nathan have on their sites. Your chosen task is your baby — you've personally nursed and nurtured it. Kids sense this and they'll handle it with care too.
Throw a curve ball. Meaning offer a task that does not line up with your current topic right now. I know this sounds strange. (I've never read or heard anyone else suggest what I'm suggesting). Normally teachers look for a task that lines up with what the kids are learning. Sure, I do these "tasks" too, but I really call them "exercises." Exercises help you practice the skills you're learning. The tasks that this post is referring to are problem-solving tasks, and true problem-solving has no prior diagnosis and certainly no given prescription. Don't do Taco Cart right when you're teaching Pythagorean Theorem. Unless you want to do it as an exercise, then sure, go for it! The beauty of this is you can reach into your folder of best tasks, close your eyes, and pick one! Be a rebel, break the rules. (Don't forget it still has to be an appropriate level task.)
Custom tailor the lesson. This is hard work. I don't care if His Holiness the Dalai Lama himself wrote the lesson, I still need to tweak it so it works for me and my kids.
Great lesson but terrible handout. I see this all the time. Take the time to re-type it. Is there wasted space or not enough? How's the font size, the heading, the outline? Can you improve on the graphics? Are students asked to work on page 2 but keep having to flip to page 1 to see the sketch or data?
Do you have to pass out the handout at all? How about starting from scratch as in having the kids take out their own paper to create data and meaning for themselves? Remember that any question that appears on a handout may potentially rob a kid's opportunity to ask that question for herself. There are certainly good handouts that have just the right amount of information and provide easier access points for kids. Please create them.
What level of technology is involved? Disaster abounds when an activity requires at least 15 computers and you only have 5. Adapt it or scrap it. No more than 2 kids should have to share a computer. Will the server crash if everyone got on the system? Did you review the YouTube video for all the potential peripheral garbage and comments that might be on there? To be safe, how about you projecting the video from your teacher computer instead? And I need to add here that I beg you not to incorporate technology into a lesson for technology's sake. Technology should enhance the student's learning. A shitty lesson on the interactive whiteboard is still a shitty lesson.
Have You Had Your Math Munch Today?
I read Math Munch's latest post yesterday.
Today my students sketched out their birthdays inspired by the post. Just as Brandon Todd Wilson limited himself to only one hour to work on each day's number, I gave my students exactly one class period to do theirs. The perfect kind of year-end lesson that does wonders for Eighth Grade-itus. Thank you to Anna, Justin, and Paul for the beautiful and passionate work that you share on Math Munch!
"Working Together" Problem
Heya, back-to-back post about a problem from Five Triangles mathematics.
When I tweeted how much I love this problem, a few people did not feel the same at all. Here are my reasons for appreciating this problem:
It's a notched up "working together" problem that I have not seen before.
It has percentages and fractions.
I can use rectangles to solve this. (I was asked on Twitter how I would solve this using rectangles, hence this post.)
I had to work on this problem. This is a big reason for me. We should assume that if we're teaching a particular math subject — Geometry, Statistics, or Calculus — that we're able to easily do all the exercises in the textbook. A set of exercises allows us to practice a particular skill. But a problem should require us to think. I hope I've encouraged problem-solving enough with my students that they value a problem more when they have to struggle with it, when they don't know immediately how to start it, when they get stuck and become frustrated, when they seek others for help, when they can leave the problem and come back to it another day.
While I'm at it, I also love the site Five Triangles in general for a couple of reasons:
The Geometry problems are simply stated and interesting. They make me pause and think, very few have been automatic gimmes.
The solutions are not posted. I really appreciate this because if they were, we might be tempted (mainly due to lack of time) to check the answers too early before we allow ourselves a chance to work through the problem and perhaps struggle with it. "Anticipating" is the first of 5 Practices that gives us insight on how students might solve the problem.
I did, however, retype the question above so it's easier to read and track information. I also numbered the paragraphs for quicker reference.
How we worked through this problem. Colors and all.
Draw a rectangle to represent the task. It has an area of 80 square units because that's the LCD of the three fractions in the problem.
Because this grid represents the task, we use it to fill in the amount of work done. Paragraph [3] is the first concrete piece of information that allows us to do this.
We continue to fill in the work done as described in paragraph [4].
Paragraph [5] is the first piece of information that allows us to figure out C's rate. Knowing that C can do 16 boxes in 8 hours means C can do the task — 80 boxes — in 40 hours.
With C's rate, we can now take on paragraph [2]. We know from the last step that C's hourly rate working alone is 2 boxes per hour or 10 boxes in 5 hours. But when working with A, C's rate is 40% faster, therefore instead of getting just 10 boxes done, C can get 14 boxes done in 5 hours when working with A.
From picture above in green, we know A and C did 24 boxes in 5 hours, and since C was responsible for 14 of those, the remaining 10 boxes were done by A.
Then A's hourly rate when working with C is 2 boxes per hour. Because this hourly rate represents a 20% increase than if A were to work alone, the math we need to do is 2 boxes divided by 1.2 to get 5/3 boxes. Solving for x in the proportion below gives us the answer that A completes the task in 48 hours.
Lastly we use paragraph [1] to figure out rate for B. We know A's alone rate is 5/3 boxes per hour, but when working with B, A's rate is 40% faster. Thus we multiply 5/3 by 1.4 to get 7/3. If A can do 7/3 in 1 hour, then A can do 35/3 in 5 hours when working with B.
The yellow boxes show that A and B can do 25 boxes in 5 hours, so subtracting 35/3 from 25, we see that B did 40/3.
To get B's alone rate, we divide 40/3 by 1.2 (because B is 20% faster when working with A) to get 100/9. Solving the proportion below gives us the answer of B completing the task in 36 hours.
Technology and Construction Papers are Cool
Big-time struggles for my 8th graders on this problem from Five Triangles mathematics.
The one student who got it also struggled, but he was good about our rule of "never tell an answer." What I gathered from seeing their boards and listening to them explain:
They wanted to find the area of the parallelogram first.
So they needed to find the height.
To find the height, they reasoned that triangle ABC was isosceles, making the perpendicular bisector AY also be the height of the parallelogram. Then they could use the Pythagorean theorem to find AY. (I can't get AB and DC to be exactly 6.00 cm.)
So I showed them the parallelogram below just to be less helpful and to remind them about assuming something is isosceles because it looks it.
Without a clear way to find the height, frustration mounted.
But major props to them for persevering as you can tell from their boards that they tried to dissect the parallelogram into even more pieces in hoping they'd find what the shaded piece would be equal to.
The next day... I let them struggle some more. They weren't seeing the key pieces (at least to me they were key), so I told them to look at the "relationships" among the pieces. They were pretty sure the diagonals of a parallelogram cut it into 4 triangles of equal area. Then they were stuck again. I then asked them to construct this parallelogram using Geometer's Sketchpad (GSP) and find the answer to the question posed. Soon one student asked, "What should the angles be?" I replied, "It doesn't say in the problem, so I don't know. But it is a parallelogram, so make sure you have the same side lengths." Without much trouble, they found the answer. They also realized that even though they may not have created congruent parallelograms among themselves, they all came up with the answer of 0.17 or 1/6.
Me: So why did I ask you to use GSP to do this?
Student: Because we couldn't do it by hand?
M: Maybe. Or maybe you didn't have enough time. But why do we use GSP in general? What's the difference between doing a construction by hand and doing it using GSP?
S: So we can move things around.
M: Right! It's dynamic! Then this is what I want you all to do. Move things around. Drag the side lengths. Change the side lengths. But while you're doing all this messing around with the parallelogram, I want you to pay attention to the numbers, the measurements.
Not long before many of them chimed in excitedly: The ratio doesn't change! I came by each kid's screen to check their work. (These are my reconstructions of some that I saw.)
To make the most of their construction (and a good problem), I then asked them to find the ratios among all the pieces that they saw. I wish you could hear them. A bunch of them kept making the same exclamations: So cool! Mind blown. While only one student found the solution by hand, the rest of them felt pretty good about their construction of parallelograms, and they discovered important relationships among the pieces. Technology came to the rescue. Here's how I used colored construction papers to help students see the relationships better.
Advantages:
Instead of having to write down or say "triangle ABC," "triangle BEC," or "quadrilateral FDGE," I can just refer to each one by color.
By not having to follow the letters of ABC or GCE, kids can focus on the visuals and see the relationships more quickly.
I can show congruence by placing one piece on top of another.
Something like this:
The diagonals cut the parallelogram into two pairs of congruent triangles. Therefore, each blue is 1/4 of whole. (I reflected each pair so they can see the congruence.)
Below left: green is 1/2 of whole.
Below right: red + yellow = 1/2 of green, or 1/4 of whole, because they share the same height and half the base.
Below right: red + pink is 1/4 of whole (same size as a blue). Since left and right images below are equal in area, and red is red, therefore yellow equals pink.
Blue + yellow (combined) is a similar triangle with pink due to AA postulate. And because their side lengths are 6 to 3, or 2 to 1, then their areas are 4 to 1. Let's call the area of pink as 1, and we learned from above that yellow equals pink, so yellow is also 1. This leaves blue to be 3.
Putting all the pieces together, we have a total area of 12, so the shaded part (red) is 2/12 or 1/6.
Add to what Robert said, your kids have enough GSP skills to use it to investigate a problem. Kudos! That's a tough trick to pull off. I did it a different way! I found constructing a supporting parallel line dissected the quadrilateral in a helpful way. http://www.geogebratube.org/student/m83241
February 10, 2014 12:10 PMfawnnguyen wrote:
Hi Kate. Yay, beautiful work!! We did this activity just last week and one of the kids asked at the start, "How do you find the area of a non-parallelogram or trapezoid [FDEG] anyway?" I replied, "Well, can you divide that shape into other shapes that you can find the areas for?" So, I saw the groups draw in that parallel line that you have. They were able to find the area of pink triangle as 1/8 of whole but struggled with finding area of blue triangle during their paper/pencil work.Thank you, Kate.