My Other Math Sites
Lessons From the Classroom
When I Got Them to Beg
A quick flip to the quadratics section in each of the six textbooks lying around here I find at least one problem about finding the width of some border. The concrete around a pool, the walkway around a garden, the frame around a picture, the border around a rug. I present to you the collage.
I don't know.
And because I don't quite know what else to do, I come up with a lame lesson idea: make the kids create a frame around a picture given a specified amount of frame, this should drive them bonkers as they won't be able to do it perfectly (not even close!), and then they'll beg me to show them the math to make this task easier. They beg, I win.
I give them the goods. To each kid:
scissors
ruler
any old picture, size 6 cm x 11 cm
a white frame, 4 cm x 7 cm (but they get 4 of these because they'll mess up!!)
My one-way conversation with them about the task. I do the talking:
Framing is very expensive. Even if you have the 50%-off coupon, it still costs a lot. For example, last year I took my son's art work that he'd done for his IB Art class to Aaron Brothers to get them framed. I wanted them matted also — you do know that matting is a fancy word for cardboard so they can charge you more, right? — anyway, guess how much the total was? Over four hundred dollars! Four-hundred-dollars-and-that's-with-the-friggin'-coupon.
I told the sales guy, "My son is not Picasso. His drawings are half crap. I don't even want them, you can keep them."
So, your job today is to be a picture framer. Show me which one is the picture... Good. Now, hold up the piece that is the frame... Good. Think of that piece of frame as gold. It's expensive.
How come I gave you 4 frames?... That's right, you'll probably make mistakes, so you get 4 trials.
Your job is to cut your [expensive gold] frame into pieces — strips — that will go around your picture. You have to use the entire 4 cm x 7 cm piece with no leftovers.
But you don't want to cut it into a million pieces either. Fewer cuts means fewer pieces to seal back together to form a frame. And it looks nicer.
Do-you-have-any-questions?-no?-good-begin.
Almost immediately, I hear:
Marissa: What do we do?
Me: I just... e x p l a i n e d...
Malainy: I'll tell her, Mrs. Win. Okay, you cut up the picture to make it fit into...
Me: What?! Cut the picture?! People bring in their most precious picture to you to frame and you cut up their picture?!
Malainy: Oohh noo. Then I'm not sure what we're doing.
Someone: Do the pieces have to be even?
Me: Have you ever seen a frame with different widths?
A Different Someone: I don't get what we're doing.
Me: Should I just speak Chinese to you guys from now on?
Yep. This is pretty much a verbatim snippet of what goes on in my last period today.
After lighting my hair on fire, they manage to work diligently.
Sure enough. About 15 minutes later they grow tired of the frame pieces. A few almost have it, but they know this is not good enough.
They speak up:
There must be a better way to do this!
I'm gonna be fired because I'm wasting all these gold frames and still not getting it right.
My pieces are thick and thin everywhere.
I always have this left over stupid piece!
And here comes the money:
Can you please show us the math for this?
Updated 04/11/13
Thank you to Christopher for sharing with me on Twitter his 3 trials:
Updated 04/16/13
Thank you to Mike Lawler for sharing this video of him working through this problem with his young son.
Des-man
Not only was this so great to reinforce slope, y-intercept, and all the coefficients, it also allowed us to talk about domain and range.
What I heard around the room (that I can remember):
Oh, I get this now! I see what changing this number does!
Oops, I made his face too wide!
His smile is crooked. But I think I'll leave it because he looks cool that way.
Ha!! I see my mistake, I said x had to be greater than 4 but less than 2. Silly me.
I want the eyes to be oval shaped though. My plan is to make 2 parabolas opening into each other.
Can we work on this in 6th period too?
When I saw two students whose graphs were circles for faces, I knew they'd copied these from Desmos gallery as we haven't — and won't — learn circle equations in Algebra 1.
I reminded them of the minimum requirements, but I told the class that they may copy equations and tinker with them to add other features, such as hair and whiskers. (I actually said "whiskers," and Lexi had to tell me, "Whiskers? On a man? You mean beard or mustache?") People don't have whiskers? Good to know.
I made my guys' eyes elliptical and tweeted it, the good folks at Desmos responded.
So cool!
I think we got a lot of mileage from this activity. It's a good sign when teacher instruction is minimal and student engagement and discussion are high.
Just in case you missed the Grand Opening of Daily Desmos about 3 weeks ago, brought to us by Michael Fenton, inspired by Dan Anderson.
Smallest and Largest
Most of my 6th graders struggled with this handout today. Only 4 of 36 students scored 8 out of 8 on it. I offered no help on this except my reading the instructions to them and reiterating that for each operation, the two numbers must be different.
I retyped this task from the Noyce Foundation.
If you teach 6th grade math or if you could share this with a colleague who does, I'd be very curious to learn how your kids might do on this. (Guess I'm now wondering how 7th and 8th graders fare on this too.)
I'm feeling disheartened and ineffective with this group of 37 kids. If I squinted really hard, then maybe I could spot just a few tiny specks of mathematical growth in them.
This teaching thing is tough.
Students Embroiled in Conway's Rational Tangles
Me: We're going to do an activity today.
Jonathan: Let me guess. It's your favorite activity.
M: How did you know that?
J: You say that about everything we do.
M: You have a problem with that?
J: No. But I've lost track of how many favorites you have.
M: And I've lost track of how many times you've talked without permission.
M: But I still love you though.
J: I love you too, Mrs. Win.
Yeah, so that was the exchange we had at the start of Algebra. Kids are used to me telling them how much I love them because I really do. It's the Monday-through-Friday kind of love that lasts from 8:25 am to 2:50 pm — at which time I say to them, "Get out of my room." They laugh at this; they must think I'm kidding.
Tom Davis did John Conway's Rational Tangles with us at last summer's Math Teachers' Circle (MTC). Reading this post (with lots of solid links) over the weekend reminded me of this fun lesson.
I haven't come across a written lesson of this done with school children though. So, here I am. It's my new favorite lesson.
Day 1
I use the two ropes given to us from the MTC training.
I ask for 4 student volunteers to come up front. The rest of the class needs to pay careful attention and record in their math journals what I record.
Important
The two ropes can be of the same color. Two colors are used in practice so it's easier for students to follow along.
The 4 people holding the robes can be identical quadruplets — who they are doesn't matter, but I'm referring to them as colored dots if and only if they move or change position.
The letters A, B, C, and D refer to the 4 positions, like goalposts, therefore they do not change.
The starting position is when the two ropes are horizontally parallel, and this state has a value of 0.
There are only TWO "moves" in this game of rational tangling and untangling.
A TWIST is when people in positions A and C switch places. Green moves underneath red's rope.
This move equals plus 1, meaning our ropes went from a value of 0 to a value of 1.
The only other move is called ROTATE. A rotate is when the 4 people move in a clockwise direction, each person taking the space previously occupied by the person to his/her left.
Now, the money question to the kids: What does the operation "rotate" do to the value of the ropes?
We know a twist = +1, but a rotate = ??
So, in the diagram just above, our ropes went from a value of 0 to what value?
The kids want to do a twist after this rotate, but they realize that the ropes are now funny — or vertically parallel — that you can't do a twist since there's no rope for yellow to go under, and green and yellow switching places does not change how the ropes look.
Because a twist can't be done, our only other choice is to rotate — which leads us to this configuration.
AHA! This brings us back to 0 because the ropes are horizontally parallel again.
Symbolically, we can record what happens with 2 rotates (R), done back to back, when we start with 0: 0 (R) -> ? (R) -> 0.
We need to test this again, so let's start at 0. Do 1 twist (T), then 2 rotates. This means the value goes from 0 to +1, then to some unknown value after the first rotate, but after the second rotate, the ropes have a value of +1 again.
0 (T) -> 1 (R) -> ? (R) -> 1
Someone suggests that the rotate operation means multiply by -1. This is a lovely suggestion as it seems to work: a twist of 0 makes it +1, then if a rotate means multiply by -1, then we have -1, then another rotate makes it +1 again.
Then we try to do 2 twists from 0, giving us +2. So if we do a rotate now, our value should be -2. This means we can then do 2 twists to add 2, bringing us back to 0. But it did not work!
We do a few more test moves. Someone suggests a rotate subtracts 2. Others suggest that it throws a negative sign on the value somehow, somewhere. The kids are struggling. One claims a massive headache from all this, to which I say, "Enjoy that, honey."
We have a few conjectures though:
Starting from 0 and doing 1 rotate puts our ropes in a weird (undefined?) state where we can't do a twist after that.
Two rotates, back to back, bring the ropes back to the same state prior to the first rotate. Therefore, we should not do 2 consecutive rotates unless we just want to waste time.
A rotate must involve a negative — how else can we get back to 0 by twisting alone?
I instruct the 4 volunteers through this entire sequence of moves below. The class and I record each step. As soon as we put in a rotate, however, and not know exactly what this move does to the value, we just have to put question marks in all these spaces.
I can't take pictures of the kids doing this while also teaching them, so I've re-created this at home with a shoe box and 4 well-behaved binder clips that act has the rope holders.
Step 1: Start at 0.
Step 2: Do 1 twist. Value now is 1.
Step 3: Another twist. Value = 2.
Step 4: Another twist. Value = 3.
Step 5: Rotate. Value = ??
Step 6: Twist. Value = ??
Step 7: Rotate. Value = ??
Steps 8 & 9: Twist and twist again. Value = ??
Step 10: Rotate. Value = ??
Step 11: Twist. Value = ??
Step 12: Twist. Value = 0
Kids realize that if the last two twists got the ropes back to 0, then Step 10 must have a value of -2, and Step 11 is -1.
After about 20 minutes of doing the dance with the ropes and agonizing, a couple of geometry kids figured out what a rotate does to the value of the ropes. Algebra kids did not have enough time, so they'll continue their investigation on Day 2. Because I only see my 6th graders one period a day (instead of 2 periods/day for algebra and geometry) and they being younger, I told them what "rotate" does mathematically. There will still be plenty of math for them to do on Day 2.
Day 2
It's more fun when the kids can participate instead of just watching the 4 kids in front of the room. I go to Lowe's to pick up the ropes for about $12.
Kids will be in groups of five, four are holding the ropes and doing the moves, one person records and oversees that everyone in group is moving appropriately. Each group gets 2 ropes, one of each color, and each rope is about 7 feet long.
All the groups will first follow the same set of crazy tangle moves that I give them. Something like, "Start at 0, twist 4 times, rotate, twist 2 times, rotate, twist 3 times, rotate, twist 5 times. Okay, now figure out how to get back to 0."
(Algebra kids still need to figure out what a rotate does to the value of the ropes before they break out into groups.)
When they figure out my tangle, I'll have each team create their own tangle and undo the mess. Of course they'll have to record all the moves from 0 and back to 0 symbolically.
How will your kids figure out what the "rotate" operation does?
Update 03/13/12
As planned, I had the kids in groups of 5 and made this tangle: Start at 0, twist 3 times, rotate, twist twice, rotate, twist 5 times. Then they had to untangle this and get back to 0.
How the kids persevered through this entire problem was really amazing.
They hugged each other and jumped for joy when they untangled the ropes. Especially touching was the group that was the last to solve the problem — wish I'd captured it on camera/video.
This group was first to find the solution. (They had to create one of their own after this.)
If above video is not enough to convince you to do this with your kids, here's a tweet from Sam this morning. Imagine that — this activity blew young Sam's brilliant mind.
Math Taboo Game
Pretty sure I lied to my algebra students when I announced abruptly, "Let's play this game. It's a lot of fun!"
I had never played the game before as I just thought of it when I spoke the words. (They were doing polynomial factoring and were being so nice and quiet. I can't stand "nice and quiet" in my math class, so I had to disrupt them and wanted to play a game.)
I thought of playing Taboo using math vocabulary. In case you're not familiar with it, the object of the game is get your teammate to say a certain word on the card without using the "taboo" words. For example, describe VEAL without using the words CALF, YOUNG, PARMIGIANA, CUTLET, BOX.
My instructions:
Take out a piece of paper, fold it into quarters and tear neatly so you have 4 small pieces of paper.
Open up your math book and look for vocabulary words that we've covered already.
At the top of each piece of paper, write a word (or phrase) that you want people to describe, box this word up.
Then underneath this word, write 4 taboo words that the describer may not use.
Don't share what you're doing, wouldn't be fun if others saw what you wrote.
I need each person to complete 4 of these.
When done, fold each piece of paper exactly in half — like this (you have to show them) — and drop them all in this bucket.
A few simple rules:
Class is divided into 2 teams, Team X and Team Y.
Team X goes first: one person from Team X comes up to front, reaches into bucket to get one slip of paper and has 60 seconds to describe as many words as possible to the teammates.
Teacher stands next to the describer to make sure none of the taboo words or the main word itself is said — round is over if this happens.
Skipping a word is not allowed.
Hand gestures are okay (one describer today put his arms out in parallel fashion to get his teammates to say "perpendicular" — who's his math teacher?
Teacher reserves the right to help out whichever team she likes better.
So, yeah, we had a ton of fun. It was the last period of the day, and they didn't want to leave when the bell rang!
This went so well that I'll make a "real" game out of this. I'll print the words onto mailing labels. Then I can stick them on the back of playing cards so they are shuffle-able.
One Rod Tall
I’ve written before about reading books to my kids and following up with an activity. I read the poem One Inch Tall to my 6th graders as we’re studying ratios and proportions.
One Inch Tall
If you were only one inch tall, you’d ride a worm to school.
The teardrop of a crying ant would be your swimming pool.
A crumb of cake would be a feast
And last you seven days at least,
A flea would be a frightening beast
If you were one inch tall.
If you were only one inch tall, you’d walk beneath the door,
And it would take about a month to get down to the store.
A bit of fluff would be your bed,
You’d swing upon a spider’s thread,
And wear a thimble on your head
If you were one inch tall.
You’d surf across the kitchen sink upon a stick of gum.
You couldn’t hug your mama, you’d just have to hug her thumb.
You’d run from people’s feet in fright,
To move a pen would take all night,
(This poem took fourteen years to write—
‘Cause I’m just one inch tall).
Then I asked them to write their own poem in similar fashion (structure and style) using a unit length of their choice other than “inch.”
We agreed on the following guidelines:
minimum 18 lines, however many stanzas, no more than one page
rhyming is fun and recommended, but not necessary
typed up, size 12 font, no funky-impossible-to-read-annoying font
must be illustrated by hand, stick figures are okay as teacher can’t draw either
poem title and heading on paper
objects in the poem must be reasonably proportional
[Original post had more student samples, I’m just sharing one here.]
One Foot Tall
by Caden
If you were one foot tall, you would only be two pencils long
You would be barely taller than a math book
You could ride a big shade hat down a brook
You could sleep in a school backpack
You wouldn’t be able to reach the door handle
If you were one foot tall
If you were one foot tall, a roof would be a cliff
An iMac would be a flat screen TV
A sturdy folder would be a surfboard when riding in ferocious winds
A bathtub would be a hot tub to rest in
A Dalmatian dog would be a horse you could ride away on
If you were one foot tall
If you were one foot tall, a dog’s bed would be a perfect size
A desk chair would be a lounge chair to sit and rest in
The shrubs in the backyard would be a small jungle
A grape would be a plum
A kitchen sink would be a nice bathtub
If you were one foot tall
Speaking of reading and books and math, hot off the press is Nico Rowinsky‘s new ebook, Sally Strange. Nico clearly has a good pulse on middle school kids — he writes with heart and lightness and allows the mathematics to weave ever so gently through the pages. His Sally Strange is an all-too-familiar 7th grader in our classroom. Get it for yourself, for a friend, for a young friend, for your school library (when the hard copy comes out).
Stack 'em High
My algebra kiddos are doing Dan Meyer's Stacking Cups because Andrew Stadel did the lesson and wrote glowingly about it. But Andrew used only one-size cups, I used three different sizes.
Just eyeballing
I ask students to look at me, look at this 12-oz Styrofoam cup that I'm holding, and estimate how many cups they would need to stack to reach my height. I tell them I will not answer any clarifying questions regarding this, "just make your estimate in whatever way you think I mean by this." (Their hands shoot up anyway, but I remind them I won't answer any questions right now. It's clear that they want me to define "stack.")
They write their answers on a quarter sheet of paper. Here are their 29 estimates, the median at 24 cups.
Given the heights
Then I tell them my height is 163 cm with the flat shoes that I have on. I carefully measure the cup's height in front of them, we get 11.25 cm.
Equipped with this knowledge, I ask the same question as above. Their 28 answers yield a median of 14 cups. Of course Dan had already anticipated this — most students just divided my height by the height of the cup.
Stack 'em like this
I now ask them what it was that they'd wanted to ask me earlier. Sure enough Eddie says, "By stacking do you mean bottom-to-bottom, then top-to-top, or... one inside another?" I give him some cups to show me. At this time at least 2/3 of the kids admit that they answered the previous questions believing that I meant to stack the cups the way Eddie just described formerly. (This is consistent with the low guesses we see in the top image.)
I ask the next question, "Okay, I need you to answer the same question again of how many cups it'll take to reach the top of my head, but you now know exactly what I mean by stack, and you also know my height and the cup's height. Here, I'll even stand on this table with 6 cups stacked at my feet so you can see. Go, give me a number.
Here are their 27 estimates, and 113 is the median.
We're just getting started
I randomly pair kids up. (Normally they are in groups of 3, but I think it's better to be in pairs for this activity.) I give each pair 6 cups. They have the last 25 minutes of class to figure out:
The equation for this problem
The number of stacked cups for my height
Some groups need help with finding the y-intercept. A few groups don't know where to begin. I ask them some questions and walk away. They plan to nominate me in June as their most non-helpful teacher. Whatever.
I like this group's drawing, even though the lip and body of cup do not add up correctly.
Using their equations
The majority of the groups figure that the lip of the cup is the slope, but many groups also think that the full height of the cup is the y-intercept. Using their equations to figure out the number of cups, they give me these numbers.
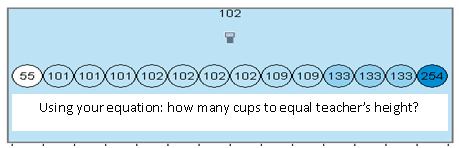
Not too shabby. My equation yields 102 stacked cups to reach top of my head, and that happens to be the mode and median.
And the actual number of cups is...
This is the moment they've been waiting for! I have 81 cups stacked already when the kids come in the next day, then they count out loud as each additional cup is added to reach my height. Our principal is paying us a visit today, and he keeps telling me how impressed he is with how engaged the kids are and how hands-on the lesson is. He helps with the countdown too and officially announces that it takes 100 cups to stack up to my height! (Three groups whose estimates of 99, 101, and 102 are having pizza with me next week!)
Getting our principal in on the fun
Working backwards. I tell the kids that it takes 116 cups to reach the top of our principal's head. How tall is he? Their answers give a median and a strong mode of 184 cm. His actual height is 183 cm!
Twice the volume and half the volume
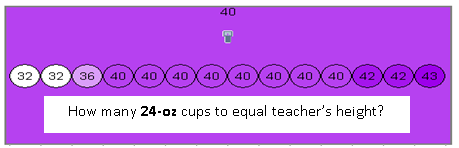
Just when they think they're done, I pull out the 24-oz and the 6-oz cups. It's not often that I hear them shriek in delight to do more math! The pair of students now gets only 3 cups of each new size. They go to work.
My height is 40 24-oz cups and 126 6-oz cups. Their calculations are great for the big cups, not so much for the little ones.
This ranks up there as one of my favorite lessons. Thanks much to Dan for another fab activity. But due to us having already passed linear equations, I honestly would not have done this lesson now without Andrew's push.
Updated 02/06/13
Eight more kids will join me for a pizza lunch for getting the equations to the 24-oz cups correctly. And here's a pic of me and the 3 stacks. The boys are 6th graders helping me hold up the stacks.
The Question Was Mine, but the Answer Was All His
The algebra kids have been doing a lot of graphing inequalities on the number line, and the geometry kids have been doing a bunch of a-squared-plus-b-squared-equals-c-squared for their Viewmongus lesson.
So I'm looking at my geometry kids and thinking: Hmmm... I wonder if you know how to graph an irrational number on the number line.
I ask them to locate sqrt(7) on the number line. Two students pull out their calculators. The rest are scribbling and erasing, doodling too I suppose. They know sqrt(7) is somewhere between 2 and 3.
Five minutes pass quietly.
Another five minutes, their faces grow longer. Gabe brings his journal up to me. He writes:
You could create a right triangle with a vertex at 0 and the side being sqrt(7) going along the number line. The other vertex would be the point where the sqrt(7) is located.
I nod my head but ask, "Want to help me understand what you wrote with a picture?"
He comes back with this sketch. I tell him, "I see. Something to do with right triangles. Okay. But you know that I still don't see how you arrive at sqrt(7) right there, right? I think you're on to something, Gabemeister."
Enough individual think/stuck time has passed, I put them into random groups of three. I walk around, they're talking about the problem, but I'm not seeing much on the whiteboards. Maia [bottom right] thinks she's funny. Gabe gets himself a compass.
I'm watching the clock. Jack wonders if he could just make a number line for irrational numbers only. You know, 0 here, then sqrt(1) here, then sqrt(2) here, then oh never mind. Gabe looks busy with his compass. His group mates are observing him carefully and listening to him mumble.
Time to nudge them along. I ask, "This question that I'm asking you of where is sqrt(7) or sqrt(any irrational number) on the number line came from my watching you in the last activity. What were you doing in last two days?"
They burst out:
Aspect ratio thingies.
The diagonal of the TV!
Mathalicious!
Right triangles!
Pythagorean theorems — but this [number line] is not a right triangle!
Viewmongus!
The diagonal of the TV is the number line!
I say nothing more and continue to walk around. Now I'm seeing more on their whiteboards.
All the groups are working with right triangles, but I'm unable to take more pictures of their work as I'm now with Gabe's group and listening to him explain how he thinks he has the answer.
He goes over his drawing above step-by-step by drawing another similar one.
I'm retelling his story using Geometer's Sketchpad.
Step 1: Draw an arc of radius 3 units.
Step 2: Draw an arc of radius 4 units.
Step 3: Draw the line y = -3.
Step 4: Draw a perpendicular line (pink) to the red line where it intersects blue arc.
Step 5: Sharing this final step right now with you makes me tear up.
Tomorrow Gabe will get to share his way of finding sqrt(7) on the number line with his class.
Then maybe I'll ask the class to try finding sqrt(11), sqrt(10), sqrt(bring-it-on-Mrs.Win-we-got-this). Maybe they'll have fun doing this.
I'd posed a question that wasn't lined up with the curriculum. It just came to me as I was watching my kids do math. But the question lined up with my gut, and my heart went along and said, Do this because it'll remind you of why you love this job.
Lego Pieces and Feasible Region
This afternoon I came across a tall stack of Lego® boxes stored in my son's closet; they reminded me of a lesson.
(My son just turned 20 three days ago. I can still see him playing with his Lego sets for hours on end when he was younger. And when he ran out of floor space in his room, he took over our entire living room, and we were happy to let him.)
Simple lesson — (I was looking around and this site cited the Mathematics Teacher, Vol. 92, No. 2 February 1999 titled "Promote Systems of Linear Inequalities with Real-World Problems" as source for this problem.)
You own Funky Furniture, a store that makes tables and chairs out of Lego pieces to sell. A chair is made of one large and two small pieces. A table is made of two large and two small pieces.
Currently you have 8 small Lego pieces and 6 large ones. If the profit for a table is $16 and for a chair is $10, then how many tables and chairs should you make to maximize profit for your Funky Furniture business?
I know there are a ton of "systems of inequalities" problems out there, but playing with Lego pieces is just more fun. Students can see the "tables" and "chairs" as they build them. I have the kids work in pairs, so each pair gets a Ziploc bag of 8 small pieces and 6 large pieces. Nobody leaves my room until all the pieces are back into the baggies and returned.
If you don't have Lego, maybe the kids can bring theirs in? There's ebay. Or you can just use centimeter cubes and inch cubes, or dice and cubes, or Cuisenaire rods and round counters. Or you can just print small and large rectangles on construction paper for them to cut out — flat models are better than no models. Anything they can manipulate is fine.
We'll be ready for this lesson next week as we just wrapped up systems of linear equations right before break.
And I just remember this fun problem about Mrs. Murphy's Missing Laundry. Have you seen it? Here's the handout. There's no manipulative involved, but kids like to solve mysteries too.