Stack 'em High
My algebra kiddos are doing Dan Meyer's Stacking Cups because Andrew Stadel did the lesson and wrote glowingly about it. But Andrew used only one-size cups, I used three different sizes.
Just eyeballing
I ask students to look at me, look at this 12-oz Styrofoam cup that I'm holding, and estimate how many cups they would need to stack to reach my height. I tell them I will not answer any clarifying questions regarding this, "just make your estimate in whatever way you think I mean by this." (Their hands shoot up anyway, but I remind them I won't answer any questions right now. It's clear that they want me to define "stack.")
They write their answers on a quarter sheet of paper. Here are their 29 estimates, the median at 24 cups.
Given the heights
Then I tell them my height is 163 cm with the flat shoes that I have on. I carefully measure the cup's height in front of them, we get 11.25 cm.
Equipped with this knowledge, I ask the same question as above. Their 28 answers yield a median of 14 cups. Of course Dan had already anticipated this — most students just divided my height by the height of the cup.
Stack 'em like this
I now ask them what it was that they'd wanted to ask me earlier. Sure enough Eddie says, "By stacking do you mean bottom-to-bottom, then top-to-top, or... one inside another?" I give him some cups to show me. At this time at least 2/3 of the kids admit that they answered the previous questions believing that I meant to stack the cups the way Eddie just described formerly. (This is consistent with the low guesses we see in the top image.)
I ask the next question, "Okay, I need you to answer the same question again of how many cups it'll take to reach the top of my head, but you now know exactly what I mean by stack, and you also know my height and the cup's height. Here, I'll even stand on this table with 6 cups stacked at my feet so you can see. Go, give me a number.
Here are their 27 estimates, and 113 is the median.
We're just getting started
I randomly pair kids up. (Normally they are in groups of 3, but I think it's better to be in pairs for this activity.) I give each pair 6 cups. They have the last 25 minutes of class to figure out:
The equation for this problem
The number of stacked cups for my height
Some groups need help with finding the y-intercept. A few groups don't know where to begin. I ask them some questions and walk away. They plan to nominate me in June as their most non-helpful teacher. Whatever.
I like this group's drawing, even though the lip and body of cup do not add up correctly.
Using their equations
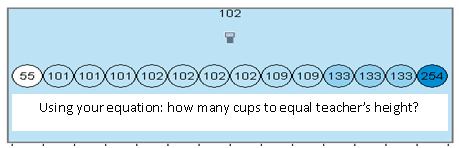
The majority of the groups figure that the lip of the cup is the slope, but many groups also think that the full height of the cup is the y-intercept. Using their equations to figure out the number of cups, they give me these numbers.
Not too shabby. My equation yields 102 stacked cups to reach top of my head, and that happens to be the mode and median.
And the actual number of cups is...
This is the moment they've been waiting for! I have 81 cups stacked already when the kids come in the next day, then they count out loud as each additional cup is added to reach my height. Our principal is paying us a visit today, and he keeps telling me how impressed he is with how engaged the kids are and how hands-on the lesson is. He helps with the countdown too and officially announces that it takes 100 cups to stack up to my height! (Three groups whose estimates of 99, 101, and 102 are having pizza with me next week!)
Getting our principal in on the fun
Working backwards. I tell the kids that it takes 116 cups to reach the top of our principal's head. How tall is he? Their answers give a median and a strong mode of 184 cm. His actual height is 183 cm!
Twice the volume and half the volume
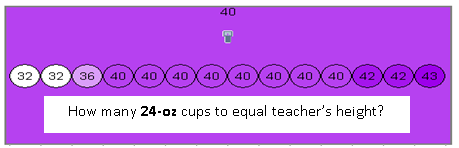
Just when they think they're done, I pull out the 24-oz and the 6-oz cups. It's not often that I hear them shriek in delight to do more math! The pair of students now gets only 3 cups of each new size. They go to work.
My height is 40 24-oz cups and 126 6-oz cups. Their calculations are great for the big cups, not so much for the little ones.
This ranks up there as one of my favorite lessons. Thanks much to Dan for another fab activity. But due to us having already passed linear equations, I honestly would not have done this lesson now without Andrew's push.
Updated 02/06/13
Eight more kids will join me for a pizza lunch for getting the equations to the 24-oz cups correctly. And here's a pic of me and the 3 stacks. The boys are 6th graders helping me hold up the stacks.