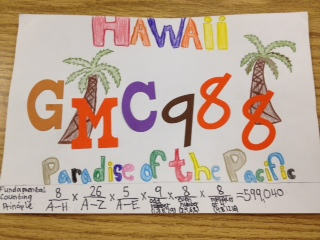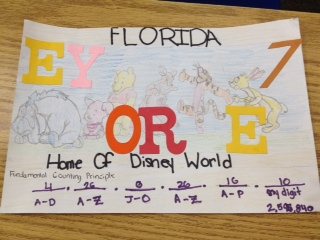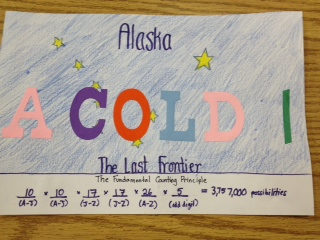Why Wait for Calculus?

(I just had my very best lesson yesterday, on a Friday, thank you. I feel almost brilliant right now. And I only feel like this once every 47 years, so please stay and read this post!)

My own kids tell me they will stock up their dorm rooms and apartments with junk food and soda when they move out to make up for these years of deprivation. (And this is supposed to make me feel bad.) So when I intentionally bring home a snack, like this bag of kettle corn, I usually find it empty within 24 hours. But seeing the empty bag made me think of a volume activity that I could do with my 6th graders with all these other bags of Orville Redenbacher's popcorn.

But the activity I had in mind — maximizing the volume of a box — is commonly done in a pre-calc or calculus class. These are my 6th grade babies. But didn't we do okay with approximating the volume of a torus via my doughnut lesson? So, why can't we do this too? I have to get rid of the popcorn.

I randomly assigned the kids in pairs, gave each pair two sheets of white copy paper. I told them to use one paper at a time to make a box — the goal is to make the box as big as possible so it'll hold the most popcorn. But the box must be made simply like this: cut off 4 corners from the the paper, then fold up the sides and tape them together. I used a half-sheet (so they couldn't duplicate mine) to demonstrate what I meant.

They quickly went to work. A few students were NOT cutting off square corners, so the top edges of the sides didn't line up. Two groups folded in their papers, in addition to cutting off corners, so they had to re-do.

Ryan and Annamaria wanted to make a shallow box. Ryan said, "... it doesn't matter how high it is."

Rapha and Cristian made the biggest corner cuts that I saw in the first round.

Mike's and Roy's first box was the shallowest in the class, but they changed their mind for their second box.

With 10 minutes left in our first hour together, I asked the kids to measure the box and find the volume. They had no trouble with this since we did the doughnut. They recorded the volume inside each box, and I tacked them on the board. (The butter seeped through in few of the boxes.)

Well, that was fun. I pointed out that two of the bigger boxes were over 1,000 cubic centimeters. The bell rang. I said, "We'll wrap up this afternoon."

I didn't know what I was going to do to "wrap up" the lesson. The microwave actually overheated — my room stank of greasy popcorn.

There was a confidence in me, however, that the kids would help me figure out how/where this lesson could go next. I began the afternoon hour by going over what they'd learned in the morning. They said:

The four corners must be of the same size. (I never told them this in my instruction.)

Each corner must be a square. (I didn't tell them this either. Not everyone was convinced of this, so I cut non-square corners to show them.)

There was a limit to how big the square could be. (I loved this! And this made me ask, "Is there a minimum to the size of the square?" Their eyes squinted, almost as if they were trying to "see" how small these corner squares could get. One kid said, "No. Technically, no.")

The volume numbers that people wrote down could be wrong.

By then they understood the different boxes and their volumes depended on the size of the corner squares that would get cut off. We focused on this. I asked them to draw a 10 x 12 rectangle in their math journal. We removed 1 x 1 corners from this rectangle and found the volume. I guided them through the next 2 x 2 corners. They continued on their own.

Then I gave each kid another white piece of copy paper. We measured the length and width of the paper and agreed that the paper was 28 cm x 21.5 cm. I asked them to build a systematic table like the one they just did in their journal. I said something like this, "Because you now know how to figure out the volume without actually cutting and making the boxes, see if you could figure out what size square the corners should be to maximize volume."

I saw kids high-fiving each other, "The corner has to be 4 by 4!" Rapha and Cristian beamed after congratulating each other, "That was one of the boxes we made!" We ended class with that. I swore I felt myself tearing up.

On Monday we'll play around with this applet.

And we'll ask Wolfram Alpha to take the first derivative of the volume for us. (I'm pretty sure the class could write this equation V = (28-2x)(21.5-2x)(x) for me to enter into WA.) Well, I actually just did it, and WA gives the side of our corner square as approximately 4.01965. My kids got 4 — pretty damn good for 6th grade brute-force math. Now that I'm writing this, however, I am really most proud of how well the kids had worked together. I randomly paired them up — a handful of the pairs were like the odd couples: high/low, shy/outgoing, squirrelly/quiet, jock/nerd, princess/cowboy. There was not a whisper of whine when their names were called to pair up. How did I get so lucky?

A Famous Bridge Problem

So I looked in the back of our geometry textbook, curious to see what was there — hadn't ventured this far back before and because we'd just finished with the State tests — and I saw the Königsberg Bridge problem!

I was all excited because what little I know about graph theory I find very interesting and useful. I found three lessons under the heading Discrete Mathematics:

1. A Famous Bridge Problem, pages 676-678

2. A Traveler's Puzzle, pages 678-681

3. Minimizing the Cost of a Network, pages 681-683

I thought, This could be my geometry lesson for the entire week!!

But half way through reading the first page of A Famous Bridge Problem, I came to this paragraph:

Euler reasoned that in order for a person to travel every bridge once and return to the starting point, every vertex must have an even valence. This is because a person traveling into a vertex must also leave it.  So the edges must be paired, one "in" with one "out."

It got better. Or a lot worse, actually.

In the 7-bridges problem, none of the vertices has an even valence, so a circuit over all 7 bridges is impossible. However, if two more bridges were added, giving the 9 bridges as shown at the right, then every vertex has an even valence, and a circuit over all 9 bridges is possible.

Then, finally, right before the Exercises section on the next page, a question is posed:

Can you find an Euler circuit for the graph of the 9-bridges problem?

The answer to this question, printed in my teacher's edition, is Yes.

What?!! Really?!! This textbook just gave away the answer [... so a circuit over all 7 bridges is impossible] to what I thought would be a natural first question that I would pose to my kids: Can you walk in the city of Königsberg so that you will cross each bridge exactly once?

Just like that, in one swift sentence [... every vertex must have an even valence], McDougal Littell not only gave the answer but also decided not to give students an opportunity to reason it out for themselves.

I searched Google and picked this image, copied and pasted onto a Word document with nothing else on it.

I gave the students a brief history on the Königsberg Bridge problem and reintroduced them to Euler.

Question #1: Can you walk in the city of Königsberg so that you will cross each bridge exactly once?

Bobby: Yes!

Josh: This is too hard!

Jacob: Don't say that. Mrs. Nguyen loves it when we say that!

Zach: The answer is no.

Taj: No.

I walked around the room. All but two students answered NO to the first question. What they said and what their papers looked like:

(Many): I tried a few times, can't get it to work. I'll try a couple more times.

Michael: You'd have to have equal number of bridges evenly.

Bobby: I know I said yes, but I can't replicate, repeat it.

I had students number the bridges, then I posed question #2: What if bridge 2 got destroyed, no longer there, can you walk in this city so that you will cross the remaining six bridges exactly once?

Again, they tested more routes and wrote NO for their answer.

Question #3: Suppose a new bridge gets built to replace the collapsed bridge 2, where should it be built so a person can walk through the city crossing each bridge exactly once.

Michael: I perfected my theory!

Me: What was your theory?

Someone said something to him that I couldn't hear.

Michael: Okay, maybe not. But I discovered something else.

This is a clip of Michael explaining his thinking.

Slater explained why he'd build a new bridge next to (parallel to) bridge 4.

It made me happy that Austin called me over so he could explain his answer. Normally he's shy about sharing his work.

Colin made more sketches than anyone else. He tried a lot of different paths, and this is him explaining his placement of the new bridge.

I recorded all the possible placements of the new bridge (to replace bridge 2) on my sketch on the projector — there were 5 different locations that were shared.

Bobby normally is slow to leave class, today was no exception. He came up to the board and started talking.

Tomorrow we'll talk about vertices and edges and valence and convert our Königsberg Bridge into a network diagram. We'll practice drawing and exploring more of these diagrams. And maybe my kids will generalize that "every vertex must have an even valence." And maybe they won't. But I think today I gave my kids a chance to think about math in their own language.

Barbie Bungee

I bought a 1-lb bag of rubber bands for my Barbie Bungee activity today.

We should have done Barbie Bungee earlier in the year while learning linear equations and lines of best fit, but better late than never. My collection of Barbies could use some refurbishing work — they get used so much each year for this activity and for our lesson on proportions.

OBJECTIVE: Create a bungee line for Barbie to allow her the most thrilling, yet SAFE, fall from a height of 3 meters.

I randomly assigned students to groups of three. Each group got their own Barbie and 7 new same-size rubber bands. My instructions:

1. Measure Barbie's height. Record this as rubber band length of 0.

2. Connect 2 rubber bands with a slip knot.

3. Wrap one of the two rubber bands tightly around Barbie's ankles.

4. Drop Barbie, holding the rubber band level with the meter stick.

5. Record Barbie's fall using the lowest point her head reaches in centimeters. This number is your rubber band length of 1. (The rubber band around her ankle is not counted in the length of the line.)

6. Add another rubber band, drop Barbie, and record. Do this for a total of six rubber band lengths.

Measuring: They quickly went to work. (We're lucky to have good weather here pretty much year-round because I need some students to be outside whenever we do projects like this — they need to spread out to do the work.)

Graphing: The groups graphed rubber band lengths vs. distance of fall. Then they drew in the line of best fit. From this line, students predicted the number of rubber bands for Barbie's bungee line that would be thrilling enough for her 3-meter jump without cracking her head open!

Once groups made their prediction — written on their papers and on the board — they may not change it. I had taped a small ruler to that rod to mark the 3-meter height. I can't have students on the ladder, so that's me getting ready to drop a Barbie. (The numbers on the left were their initial guesses before doing anything else.)

This was a blast!! I had two kids lying on the ground with meter sticks to watch and measure Barbie's initial plunge; they were our judges. We clearly had a winning jump when one group's Barbie came within 2 cm of the floor. They asked if they could get a second chance, so all 10 dolls had another jump after adjusting the number of rubber bands on the bungee line.

What I heard around the room

I noticed the centimeters went up by 10 on average.

Her height is the y-intercept.

Nine rubber bands is approximately 100 cm, so we need...

Stop stretching the rubber bands, you're gonna ruin our estimate!

Each meter stick is 98 cm. (His two teammates did not say anything when they heard this!)

I have to re-do our graph. I stuck it too close to the top, and the line of best fit has nowhere to go.

You're not supposed to connect the dots!

This was so much fun!

Oh, I didn't realize how stretchy the rubber bands got. (To which another student said, "Hello, it's rubber."

Ken is heavier [than Barbie]. We forgot this.

Hair centimeters! She was that close!

Notes

Barbies are Barbies. My kids are used to handling the dolls, a few of them have no clothes on (I got many of them on eBay). But I start every lesson with my usual warning that if I see anything remotely suggestive or derogatory done to the dolls, the student would be sent to the office and not be able to return to my class until I spoke with his/her parent. There has never been a problem in the last 8 years. The same applies to the rubber bands.

Handout 

Circles Galore

This lesson is from MARS. Using graphics from the original source, I created this recording sheet.

But instead of passing out the worksheet and starting right in like I had intended, I placed the stack in my desk drawer and decided to ask the kids to follow my instructions to create the diagrams.

I gave each kid one sheet of unlined paper and a compass. These were my instructions to them, and I followed along also.

1. Put a dot in middle of paper.

2. Draw a large circle using the dot as its center.

3. Draw in the diameter.

4. On this diameter, mark half the radius. (I could ask them to bisect the radius, but to save time, we just estimated "half" using a ruler.)

5. Now draw a circle, centered at this half-radius mark, using a radius half that of the original circle, draw two adjacent circles along the diameter.

6. Shade in the outside of the two small circles — their drawings should now look like Stage 1 on worksheet.

We stopped here, and I asked Question 1) What fraction of the large circle is shaded? They quietly did their thing.

After seeing about half of the kids finished answering this question. I said, "I know not everyone is done with #1, which is perfectly okay, but I'm going on with my instructions because some people are done, and I need you to follow along. Then if you need to, you can go back to #1."

I repeated directions 4 and 5 above, and before I asked Question 2, Josh said, "What fraction is shaded now?" They went to work again.

I then repeated the instructions to get their drawings to Stage 3. However, our compass can't make a circle smaller than 0.5-inch radius, so we freehanded them in. Everyone knew next came Question 3) Now, what fraction is shaded?

And Josh immediately asked, "Are we doing this again, make even smaller circles?!" We drew in the next 16 shaded circles for Stage 4.

You guessed it. Question 4) What fraction of the large circle is shaded? I asked them to work alone on the questions, but that they would have a chance to discuss with other classmates during the last 15 minutes of class. They plugged away.

Then the talking began; and there was a lot of it, so I started recording their conversations. I was more interested in those who did not get 1/2 for Question 1. I happened upon Zach telling his two classmates that the answer was 2/pi:

Did you catch what Zach said? He reasoned that (16*pi) + (16*pi) = 2*pi*32 by saying "You can't get rid of stuff because we haven't done any mathematical operation to get rid of pi." I was so glad this came up! Sometimes I feel a wrong answer is just as important as the correct one.

(But I thought it was funny too how Slater reacted, "That's wrong." Then there was peer pressure, "He made me change my answer." And there was alleged copying. Then there was, "Taj showed me the way." I will miss this class.)

Daniel started the discussion with this group.

The "formula" that Daniel had trouble articulating was never written on his paper, it was all in his head. Then I noticed that he'd carried his calculations to stage 8! I was so pleasantly surprised by this that I was speechless.

Class ended and everyone agreed that the answer to question 1 was 1/2.

I passed out the worksheet above for homework, asking them to try to figure out the answers for stages 2 through 4 if they hadn't already, then to give stage n a try if they had time. Daniel never saw the worksheet to know that I'd wanted him to keep thinking of the pattern, but he was already heading there on his own.

Tomorrow we'll finish out this lesson, but I wanted to capture what we've had so far before my amnesia sets in.

Some thoughts:

1. When I search for lessons/activities for my kids to do, I always search for lessons "recommended" for kids at least one grade level above mine. Meaning, I look under 9th and 10th grade activities for my 8th graders. Why not? I could always work back from there.

2. I remember adding "stage n" to the worksheet just because there was some left over space at the bottom. This made Daniel happy.

3. I'm glad I had them draw the circles. This was a last minute decision that paid off — they made pretty sketches!

4. I learn that my kids are smarter than I am. (But let's not tell them this.) Daniel's "equation" was so elegant that he could do all of it in his head. 

5. Stage n, if we get it or not tomorrow, is icing on the cake. I feel pretty full.

Speaking of stage n. What do you think? Is there a limit that we are approaching?

Staircases and Steepness, Continued

This happened Thursday.

By Friday morning the kids who did "base times height" learned that these numbers didn't match up with the steepness ranking. They said, "That just gives you area."

So I made these sketches, and hopefully the kids understood why finding area wasn't the same as finding steepness.

Those who did not do "base times height" shared what they'd calculated for steepness:

Because almost everyone got the correct steepness ranking the day before, they knew their homework calculations had to match the order, with staircases B and E yielding the same number.

Rapha: My dad helped me. I learn that the steeper it is, the number gets closer to zero.

Jocelyn: I measured one of them wrong. Did I just get lucky then?

Ryan: I tried base divided by height first, then I changed my mind to height divided by base because it made more sense for the numbers to go up instead of down... if it's gonna get steeper.

Matt: My base minus height did not work!

Arthur: Rapha's kinda the same as Ryan's, except backwards. And if you add her step widths, you get the base.

I was on cloud nine. Then I finally said the word slope, but I never said "rise over run." We ended class with this video "Tutorial — Measure Slope Steepness" by Bruce Tremper, Director of the Utah Avalanche Center.

We had a busy but fun Friday as it was also our 3rd quarter PFO-funded Einstein pizza party. Luckily my prep period is right before lunch to allow me to leave campus to get the 8 pizzas at Costco. The weather was gorgeous and we had 10 minutes left of geometry, so I took the kids outside to play Fizz-Buzz. If you've never played Fizz-Buzz with your kids, then don't start unless you want them to constantly pester you to play the game, even when there's only a minute left of class.

Staircase and Steepness

AHHHH, I love how this lesson has turned out so far!!

Today was our 3rd day of State testing, and because I have 8th graders for homeroom, we still have three more days of testing next week. Ick.

I didn't want to cram/review again with my 6th graders today, so I thought of doing a lesson on "steepness" (adapted from Swan and Ridgway).

I began the lesson by showing a bunch of images, like these, and asked,

What do you see?

Kids' responses: going down, going up, all using their legs, exercise, at an angle.

Here’s the lesson. I purposely wrote it as if it were unfinished because I didn't want it to end on my terms. I wanted the kids' conversations and discoveries to guide me to closure, if any.

Question 1: Without measuring the staircases, put them in order of "steepness," starting with the shape with the least "steepness."

Question 2: Explain how you came up with your ranking in #1. Because you were asked NOT to measure, what "tools" or strategies did you use to make your decision?

You can see from these photos how they thought of "steepness."

Question 3: Now discuss your ranking in #1 with another classmate. Are you going to change your ranking? If so, please indicate your new ranking.

Question 4: Now discuss your ranking in #3 with a different classmate. Are you going to change your ranking? If so, please indicate your new ranking.

Six students made no change to their original ranking after talking with two other classmates, 16 made one change, and 9 made two changes.

I was already so happy to see how the activity was coming along. I didn't realize how much more I was about to learn from Question 5 and beyond.

Question 5: You may now measure the staircases with whatever tool(s) you need. Use the space below to keep track of your measurements, calculations, and notes.

A few kids asked for a protractor, most used a ruler. Most of those who used a ruler measured this length.

Me: Now that you have these measured, what do the numbers mean

Matthew: (Silent, mumbling...)

Me, pointing to staircase F: I see this has the longest length. Was this your steepest shape?

Matthew: Oh no. D was the steepest.

Me: Okay. Shape C has the shortest length. What does that mean in terms of steepness?

Matthew: I don't think these numbers are right.

I went over to Troi's desk, she too had measured the same lengths as Matthew did.

Troi: These numbers didn't do anything for me.

Me: What makes you say that?

Troi: Well, the staircases are all different sizes, you'd have to make them all the same to compare them.

She then measured the rise of each step. I left her to do so.

Rapha: I'm measuring the height, but it depends on the width too.

She didn't do any more with the two sets of numbers.

Zoe: Can you show me how to use a protractor?

Me: Sure. Which angle do you want to measure?

She pointed to the middle of the staircase. I worked with her for a little while.

I checked on a small group of boys who seemed to be using the protractors correctly.

Mike: We agree on the rest of the ranking. We're just not sure about B and E. They're like one degree apart.

Ryan, holding up two different brands of protractors: These aren't even measuring the same.

Me: Hmmm. Tools aren't perfect, are they?

I was watching the time; we had 20 minutes left of our 2-period class. I asked them for a "final answer" after whatever measurements they'd done, "Put this ranking at the bottom of your worksheet."

By then the kids who used a ruler had abandoned the tool for the protractor. Make no mistake, these kids were pretty confident that if Ryan and Mike were measuring the angles, then they ought to be doing the same. More importantly, they noticed that the angle measurements correlated with their steepness rankings.

I asked Miles first — just because he sat front row, right side — for his ranking: D A B E C F. I asked if anyone else had the exact same as Miles'. Twenty hands went up. I asked for Moses' ranking: D A E B C F. Ten hands went up for this ranking. That only left Sierra with a different ranking. (Sierra was one of six who never changed her original decision.) Because B and E do have the same steepness, all 30 of 31 kids were correct.

Now what? Somehow ending the lesson here seemed weird, even though we had a lot of good conversations. They used angles to figure out steepness. I hadn't planned this! What about the ruler?!

So I said, What if you didn't have a protractor? What if you only had a ruler? What would you measure instead?

I then defined lengths on the staircase that could be measured with a ruler so we could all speak the same language about what was measured.

I said, It was great that you figured out steepness using a protractor. But now I want you to figure out how to find steepness using a ruler. Which of these lengths would you measure? Do you need to measure more than one? And if you measured more than one, what would you do with the two/three numbers you have?

They began measuring ferociously, calculators in hands. (Yes, we use calculators all the time!) I didn't see anyone measuring the slant. I got this much from them by walking around and asking:

Base minus height.

Base divided by height.

Base times height.

Height divided by base.

I ended with, For homework, please finish measuring and calculating for all six staircases. Do your calculations support the ranking?

Troi walked up to my desk when most students had already left, Can I change? I already knew... I did base times height. That didn't work.

#peedinmypantshappy

Staircases and Steepness, Continued

Designing License Plates

Yesterday I saw this question in the 6th grade workbook:

Use the Fundamental Counting Principle to find the total number of outcomes in each situation...

12. a license plate that has 3 numbers from 0 to 9 and 2 letters.

Then an idea popped into my head that my kids could design these license plates. We've covered sample space already, and I brought up the Fundamental Counting Principle last month when the Mega Millions jackpot soared to a record high of $640 million.

I gave them instructions for the layout.

I let them research the state and start a rough sketch in their math journal.

I asked them to record on the white board what letters and digits they needed me to cut for them.

I gave each student a 8" x 12" white construction paper, reminded them this was the only one they'd get from me.

I told them their homework was to complete at least the background drawing.

I gave them one class period this morning to glue the letters and digits onto their plates. They checked to make sure their calculations were correct for the sample space.

I'm very pleased with how well these license plates turned out with only two class periods used. We wrapped up the activity by figuring out the sample space for California plates, but I also pointed out that not all possibilities could be used or some people would be driving around with plates like "1ASS29" or "2FAT46."

I am a doughnut.

I cannot eat a doughnut without thinking of Eddie Izzard. Language caution in this video clip.

Ich bin ein Berliner aside, I needed a calorie-laden lesson for my 6th graders to welcome them back into the classroom after two beautiful spring break weeks.

(We are also two short weeks from state testing and should be reviewing for the test. But who wants to do that when one can eat a doughnut instead?!)

I got the idea for this lesson from NCTM.

Estimating Volume

I held up one doughnut and a centimeter cube and asked each student to write down an estimate of the doughnut's volume in cubic centimeters. But first, I needed to tap the kids' prior volume knowledge.

Me: So, what is volume? What is the volume of this doughnut?

Julia: Length times width times height.

Me: Hmm... Where is the length of this doughnut? Or its width?

Julia: Oh...

Matt: It's the inside of something.

Sam: But that's area.

Rapha: It's the whole thing. The doughnut itself.

Matt: No, I mean the space inside.

Julia: Oh... it's how many of those cubes fit inside the doughnut!

I always dread hearing kids give me a formula for anything unless I specifically asked for a "formula," but this time I didn't break into hives.

I asked if it would be okay that I just counted the centimeter cubes in each of the solids below to find volume. The kids immediately pointed out the empty space inside and one said, You have to add like 5 to your answer to make up for the space. Another student said, More like add 10.

The class agreed that the cylinder held more cubes than the sphere and that the doughnut would be bigger than the cylinder. I told them there were 69 green cubes in the cylinder and allowed them to change their doughnut volume estimate if they wanted to.

When a centimeter cube was placed on the doughnut box, almost everyone said, Wow! (This made me happy because it showed they thought of volume as volume, not length-times-width-times-height.) They recorded their estimates for the box's volume.

Estimating Surface Area

When I asked the kids about SA, they said the outside, all-around, total area, all the surfaces, and doughnut skin represented SA. I added that the amount of glaze could also represent SA.

I told them this grid paper had 22 by 18 rows or 396 square centimeters and asked for their estimate of the doughnut's surface area.

They also recorded their estimate of the box's surface area.

Measuring the Doughnut

To manage this potentially messy lesson, the doughnut had to stay on construction paper, and all measurements had to be taken with a paper ruler.

Students took as many different measurements of the doughnut as they thought necessary to figure out volume and surface area.

They ate the doughnuts, and Cristian wanted me to take a picture of him.

We'll wrap up the lesson tomorrow and discuss approximating for volume.

No, none of my 6th graders brought up any of these -us words: torus, annulus, calculus. However, we did a lot of estimating and measuring with visual and concrete models. We each gained 200 calories from this. 

Updated 04/17/12

In my comment, I told @Peter_Price about making a cylinder similar to the doughnut; then, I found this roll of masking tape that was close in size!

My 6th graders are familiar with area, so surface area was easy to grasp. (I felt smart when I could just peel off the tape to show the side SA.) I showed them my set of vinyl nets to the geo solids also.

I needed the students to figure out how to calculate volume on their own. I used these two models because of both the CDs and the patty paper sheets are very thin.

Student A: Find the area of one sheet and multiply by how many sheets there are.

Me: There are 1,000 sheets here, so area times 1,000 gives me volume?

Student B: No, that just gives you the area of 1,000 sheets, kind of like their surface area, but you're still doing area, aren't you?

Me: It would seem so.

I told the class that finding the area of one sheet was correct. And they also knew that it was the same area as the base of the box. Then I poured out the stack of CDs and started filling its container back up one by one. (Easier than stuffing the patty sheets back in.) I said quietly. Volume is three-dimensional.

The class watched, and soon, the hands went up. Before I could call on anyone, a few students couldn't contain themselves and violated our classroom rule of waiting to be called on before talking. Two kids yelled out, The height! Then more chimed in to say, Multiply by the height!

Unders and Overs

Here's where I got the idea for "Unders and Overs."

Yesterday, my colleague alerted me that we were almost two chapters behind in our 6th-grade pacing calendar. I'm always behind in this annoying and demanding calendar, but never quite this far back. So, just like that, I told the kids we were done with Chapter 8, and let's move on to Chapter 9 — Probability!

What's the best way to start a new unit? We play a game, of course.

I ask the kids to take out a blank sheet of notebook paper, place it on their desk in a landscape layout, divide the paper into thirds, and mark each section like this:

I give each kid a bag of centimeter cubes. (We use these often for all sorts of things.)  I tell them to take out only FIVE cubes—and this is their money. The remaining cubes in the bag represent the dealer's money. I am the dealer. I tell them to be honest—because it sucks to cheat—and they may not borrow and will have to sit out if they lose their five cubes.

I explain the game: I will roll two dice; if the sum is under or over 7, then I—the dealer—pay them even money, and if the sum is equal to 7, then I pay them 3 to 1. I do a few examples to make sure they understand. I trust them to reach into the bag to take out the dealer's money if they win and to put money into the bag if they lose. They lose when they place a bet on a space that I did not roll.

I check across the room to make sure they place their bets before seeing the dice roll. These are 6th graders—they are adorable, but I wouldn't put it past them to lie about bets!

First roll: we get a 2 and a 5, so the sum is 7... the kids cheered! The second roll was under 7, they roared! The third roll was over 7, they went nuts!

They are having so much fun! I pause to remind them to think about the math. What math? And that's okay right now. The ones who are winning are betting more cubes. Leo puts one cube in each of the three spaces; Arthur tells him, "I don't think that's a good idea."  Melanie is betting on all three spaces anyway; she says this will give her a better chance of winning.

The math will turn up eventually. Let's have fun right now.

Investigating Area With Paper Folding

Last Thursday was a half-day for students because we had an open house at the event. I decided it was a good day for my geometry students to do some paper folding. I gave each student about five sheets of hamburger patty paper and these instructions:

Task 1: construct (by folding) a square that is 1/4 the area of the original square.

Everyone got it except Daniel, who didn't follow instructions and constructed a rectangle with 1/4 the area. The kids jokingly gave him a hard time. I reminded the class that Daniel's left arm was still in a cast, so squares and rectangles were the same to him.

Task 2: construct a triangle that has 1/4 the area of the original square.

Again, no problems. Everyone folded the same way.

Task 3: construct another triangle, still 1/4 the area of the original, but this triangle may not be congruent to the one you created in Task 2.

Some time passed, but not too long before Slater got it, and Zach did. They shared it with the class.

Task 4: construct a square that is 1/2 the area of the original square.

Easy-peasy.

Task 5: Construct a square that is 1/2 the area of the original square—the same instruction as Task 4—however, it must be "oriented differently."

Then I went to sit down, put my feet up (okay, figuratively speaking only), drank some water, and peacefully watched as my students slowly but surely mangled up their papers trying to create this square. They asked for more paper, and I gave them more.

Austin: What do you mean "oriented differently"?

Me: Its orientation is different.

A: That didn't help...

M: I'm not here to help you.  Not today.

Zach, waving his folded paper above his head and proceeded to walk up to me: Oh, I got it!

M: No, you don't got it.  Sit down.

Josh: I got it!!

M: No you don't.

J: But you didn't even look at my paper.

M, pretending to look: There, I looked.

I watched with satisfaction as everyone struggled with Task 5.

The kids know I live for moments like that. They are stuck, and they have to think hard.

Even Slater, a self-proclaimed math prodigy (who had elevated himself to "academic prodigy" since then), was quiet and used his pencil to calculate on paper. Even Bobby—who once claimed that he and Slater should get the same IQ score if tested—sat quietly, arms to his sides, staring at the patty paper.

The bell rang.  I told them to work on it for homework, and the hint was "right triangle."

Alex: Someone will look it up online, Mrs. Nguyen.

Me: That's their loss.

For the next day, we did Task 5 together. The smiles returned to their faces. I love teaching.

 Updated 03/26/12

I got this activity from a workshop.  At bottom of worksheet:© 2008 by Education Development Center, Inc. from The Fostering Geometric Thinking Toolkit. Portsmouth, NH. Heinemann