My Other Math Sites

Between 2 Numbers • Chewable Math • Visual Patterns

Lessons From the Classroom

2/5/13 2/5/13

Stack 'em High

My algebra kiddos are doing Dan Meyer's Stacking Cups because Andrew Stadel did the lesson and wrote glowingly about it. But Andrew used only one-size cups, I used three different sizes.

Just eyeballing

I ask students to look at me, look at this 12-oz Styrofoam cup that I'm holding, and estimate how many cups they would need to stack to reach my height. I tell them I will not answer any clarifying questions regarding this, "just make your estimate in whatever way you think I mean by this." (Their hands shoot up anyway, but I remind them I won't answer any questions right now. It's clear that they want me to define "stack.")

They write their answers on a quarter sheet of paper. Here are their 29 estimates, the median at 24 cups.

Given the heights

Then I tell them my height is 163 cm with the flat shoes that I have on. I carefully measure the cup's height in front of them, we get 11.25 cm.

Equipped with this knowledge, I ask the same question as above. Their 28 answers yield a median of 14 cups. Of course Dan had already anticipated this — most students just divided my height by the height of the cup.

Stack 'em like this

I now ask them what it was that they'd wanted to ask me earlier. Sure enough Eddie says, "By stacking do you mean bottom-to-bottom, then top-to-top, or... one inside another?" I give him some cups to show me. At this time at least 2/3 of the kids admit that they answered the previous questions believing that I meant to stack the cups the way Eddie just described formerly. (This is consistent with the low guesses we see in the top image.)

I ask the next question, "Okay, I need you to answer the same question again of how many cups it'll take to reach the top of my head, but you now know exactly what I mean by stack, and you also know my height and the cup's height. Here, I'll even stand on this table with 6 cups stacked at my feet so you can see. Go, give me a number.

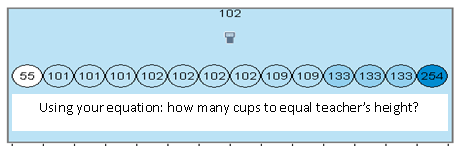
Here are their 27 estimates, and 113 is the median.

We're just getting started

I randomly pair kids up. (Normally they are in groups of 3, but I think it's better to be in pairs for this activity.) I give each pair 6 cups. They have the last 25 minutes of class to figure out:

The equation for this problem
The number of stacked cups for my height

Some groups need help with finding the y-intercept. A few groups don't know where to begin. I ask them some questions and walk away. They plan to nominate me in June as their most non-helpful teacher. Whatever.

I like this group's drawing, even though the lip and body of cup do not add up correctly.

Using their equations

The majority of the groups figure that the lip of the cup is the slope, but many groups also think that the full height of the cup is the y-intercept. Using their equations to figure out the number of cups, they give me these numbers.

Not too shabby. My equation yields 102 stacked cups to reach top of my head, and that happens to be the mode and median.

And the actual number of cups is...

This is the moment they've been waiting for! I have 81 cups stacked already when the kids come in the next day, then they count out loud as each additional cup is added to reach my height. Our principal is paying us a visit today, and he keeps telling me how impressed he is with how engaged the kids are and how hands-on the lesson is. He helps with the countdown too and officially announces that it takes 100 cups to stack up to my height! (Three groups whose estimates of 99, 101, and 102 are having pizza with me next week!)

Getting our principal in on the fun

Working backwards. I tell the kids that it takes 116 cups to reach the top of our principal's head. How tall is he? Their answers give a median and a strong mode of 184 cm. His actual height is 183 cm!

Twice the volume and half the volume

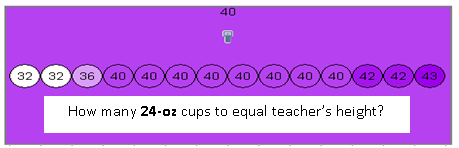
Just when they think they're done, I pull out the 24-oz and the 6-oz cups. It's not often that I hear them shriek in delight to do more math! The pair of students now gets only 3 cups of each new size. They go to work.

My height is 40 24-oz cups and 126 6-oz cups. Their calculations are great for the big cups, not so much for the little ones.

This ranks up there as one of my favorite lessons. Thanks much to Dan for another fab activity. But due to us having already passed linear equations, I honestly would not have done this lesson now without Andrew's push.

Updated 02/06/13

Eight more kids will join me for a pizza lunch for getting the equations to the 24-oz cups correctly. And here's a pic of me and the 3 stacks. The boys are 6th graders helping me hold up the stacks.

1/11/13 1/11/13

The Question Was Mine, but the Answer Was All His

The algebra kids have been doing a lot of graphing inequalities on the number line, and the geometry kids have been doing a bunch of a-squared-plus-b-squared-equals-c-squared for their Viewmongus lesson.

So I'm looking at my geometry kids and thinking: Hmmm... I wonder if you know how to graph an irrational number on the number line.

I ask them to locate sqrt(7) on the number line. Two students pull out their calculators. The rest are scribbling and erasing, doodling too I suppose. They know sqrt(7) is somewhere between 2 and 3.

Five minutes pass quietly.

Another five minutes, their faces grow longer. Gabe brings his journal up to me. He writes:

You could create a right triangle with a vertex at 0 and the side being sqrt(7) going along the number line. The other vertex would be the point where the sqrt(7) is located.

I nod my head but ask, "Want to help me understand what you wrote with a picture?"

He comes back with this sketch. I tell him, "I see. Something to do with right triangles. Okay. But you know that I still don't see how you arrive at sqrt(7) right there, right? I think you're on to something, Gabemeister."

Enough individual think/stuck time has passed, I put them into random groups of three. I walk around, they're talking about the problem, but I'm not seeing much on the whiteboards. Maia [bottom right] thinks she's funny. Gabe gets himself a compass.

I'm watching the clock. Jack wonders if he could just make a number line for irrational numbers only. You know, 0 here, then sqrt(1) here, then sqrt(2) here, then oh never mind. Gabe looks busy with his compass. His group mates are observing him carefully and listening to him mumble.

Time to nudge them along. I ask, "This question that I'm asking you of where is sqrt(7) or sqrt(any irrational number) on the number line came from my watching you in the last activity. What were you doing in last two days?"

They burst out:

Aspect ratio thingies.
The diagonal of the TV!
Mathalicious!
Right triangles!
Pythagorean theorems — but this [number line] is not a right triangle!
Viewmongus!
The diagonal of the TV is the number line!

I say nothing more and continue to walk around. Now I'm seeing more on their whiteboards.

All the groups are working with right triangles, but I'm unable to take more pictures of their work as I'm now with Gabe's group and listening to him explain how he thinks he has the answer.

He goes over his drawing above step-by-step by drawing another similar one.

I'm retelling his story using Geometer's Sketchpad.

Step 1: Draw an arc of radius 3 units.

Step 2: Draw an arc of radius 4 units.

Step 3: Draw the line y = -3.

Step 4: Draw a perpendicular line (pink) to the red line where it intersects blue arc.

Step 5: Sharing this final step right now with you makes me tear up.

Tomorrow Gabe will get to share his way of finding sqrt(7) on the number line with his class.

Then maybe I'll ask the class to try finding sqrt(11), sqrt(10), sqrt(bring-it-on-Mrs.Win-we-got-this). Maybe they'll have fun doing this.

I'd posed a question that wasn't lined up with the curriculum. It just came to me as I was watching my kids do math. But the question lined up with my gut, and my heart went along and said, Do this because it'll remind you of why you love this job.

12/26/12 12/26/12

Equilateral Triangles

Thank you to Dan Meyer for this great task idea on equilateral triangles.

Act One is this video which asks for a ranking of how well each teacher had drawn his equilateral triangle.

But as soon as I saw the video, two thoughts came up:

We're in a 0:1 classroom right now, and having the whole class come up to the big screen just isn't efficient.
I want to be in the competition! The kids will all want to do this.

So I knew this would have to be a pencil-to-paper activity in my class.

Eyeballing

My instructions to twenty 8th-grade geometry students:

Here's a blank sheet of paper for you to do this task. Be sure your pencil is sharpened. Put your name in upper-right corner.
Using only your eyeballing skill and your pencil, mark three dots in the shape of an equilateral triangle.

Gabe normally asks amazing questions that make my heart sing. Today he asked, "So you want us to draw the best equilateral triangle?" I replied, "No, Gabe, I want the crappiest one you can draw."

Now, connect the dots with a straightedge.
Pass your papers forward, I'm going to make a photocopy of your drawing so I can have a clean copy of it just in case.
While I'm making the copies, I want you to think about how you are going to decide which triangle is most equilateral.

I dashed quickly to the copy room a few doors down. I wish you wouldn't tell anyone that I'd left the children unattended for 3 minutes.

I'm now going to randomly pass the papers back, meaning you should have someone else's drawing to work with. Write your name on their paper as the "tester."
Okay, I want to know which one of you drew the bestest equilateral triangle. To do that, we need to come up with some kind of criteria, a way to test it, a way to score it. Talk to me.

They said that an equilateral triangle had to have three congruent sides or three 60-degree angles. So, I said:

I guess you'll be measuring the sides and angles. Then you get these six numbers. Do you need all six? What are you going to do with the numbers?
We know what perfection looks like: 3 congruent segments, 3 congruent angles. Let us safely assume that no one drew a perfect triangle. So how far from perfect is it? What score would it get? How fair is your test?
I need you to work quietly by yourself for now. Get your tools: ruler, protractor, compass, calculator, whatever. Then figure out a way to test for equilateralness.

Working alone

They worked diligently and carefully. I appreciated seeing this student use her ruler to extend the side length to help her spot the angle measure more accurately. Julia asked, "Measure in centimeters, right? To the tenth?"

Working in small groups

Now I'm going to randomly put you in groups of three. In your small group, share your scoring strategy. Fight about it. Defend your methods. Eventually I will ask you to choose the best method from your group to present to the class.
By the way, just because someone in your group is in possession of a drawing that you know is far from perfect doesn't mean that his/her method for testing it should be dismissed.
Oh, hey, should a larger triangle deserve more points in your scoring system? I mean, is it harder to throw down three dots that are spaced farther apart?

I moved from group to group, listening to their discussions and observing their calculations.

Watching them, listening to them, asking them questions — I didn't want to be anywhere else.

Presenting to the whole class

One by one, the groups were eager to share. They questioned each other: Why 100? Why 30? Why divide by 3

Summary of what they shared on the board. You can see that 4 of 7 groups used either side lengths or angle measures and not both.

Voting on the best one

The scoring method from Gianna's group got the most votes with 9. Gabe volunteered, "None of these is spot on. But I don't know what the best way is either." I said, "Thanks for saying that, Gabe. Me neither. But I love what you guys are all coming up with!"

Over two days, no one mentioned using perimeter or area. And I vowed not to say anything — I wanted the kids to drive this entire lesson to wherever it needed to go.

Okay, Gianna's famous now, we'll refer to her group's method as "Gianna's formula" from now on. I need everyone to go back to the triangle you have and use this formula to find a score for it.

Testing another triangle

I made another set of copies from the originals (during my prep this time) and randomly passed these out. This very diligent work was still human, and I just felt each triangle deserved another pair of fresh eyes on it.

Now, you're going to apply Gianna's formula to another triangle. This way each person's triangle gets tested by two different classmates. Record your numbers on the board.

About 7 of the 20 sets of numbers had enough variance that I had to ask both scorers of each set to re-do their calculations and/or measurements. I then took the average of the two scores.

The results

I went back to the kids' original drawings and measured all the sides (with a ruler, thanks), applied Dan's formula using this calculator and here are the results. The names highlighted in yellow share the same rankings via Dan's and Gianna's formulas. The greens are off by just one.

We thought this lesson was pretty great. Maia said, "Our way was not too bad at all.”

12/12/12 12/12/12

Drawing Rectangles Instead of Writing Equations

I don't see dead people but I see rectangles all the time.

The first time I saw a multiplication fact, like 3 x 5, as a rectangular array was after I'd graduated from college.

And because I was so very late to this game, I thought drawing rectangles must be how everyone else — at least math teachers — solved math problems.

But apparently not so. I started going to math workshops and often the teachers sitting next to me would look at my drawings and ask, "What are you doing?" I glanced over at their papers and saw mostly numbers and equations and thought, What are you doing?

So this is how I've always solved these rather mundane but classic problems.

Problem: In a town, 3/7 of the men are married to 2/3 of the women. What fraction of the people in the town are married?

My mind sees these two rectangles.

I notice that the blues have to match the pinks, so I make them match.

The answer is 12/23 of the people in town are married. (So fun to add fractions straight across.)

Problem: Danielle and Jennifer can do a job in 2 hours working together. Danielle could do it in 3 hours alone. How many hours would it take Jennifer to do the job alone?

I see a 2 x 3 rectangle as the "job," and I choose 2 and 3 because other dimensions just get messy.

It's easy then to see how much Jennifer can do.

The answer is it would take Jennifer 6 hours to do the job alone. I mean the answer is looking at me.

Problem: Dad bakes some cookies. He eats one hot out of the oven and leaves the rest on the counter to cool. He goes outside to read. Dave comes into the kitchen and finds the cookies. Since he is hungry, he eats half a dozen of them. Then Kate wanders by, feeling rather hungry as well. She eats half as many as Dave did. Jim and Eileen walk through next, and each of them eats one third of the remaining cookies. Hollis comes into the kitchen and eats half of the cookies that are left on the counter. Last of all, Mom eats just one cookie. Dad comes back inside, ready to pig out. “Hey!” he exclaims. “There is only one cookie left!” How many cookies did Dad bake in all?

Dad eats 1. Dave eats 6. Kate eats 3. So, 10 cookies are gone already.

Now, I use the rectangle to help me figure out where the rest of the cookies went. I'm reading "thirds" in the problem so I make sure I draw something that's easy to divide into thirds.

Now, I read that Mom eats 1 cookie and there's only 1 left for Dad. So the last three white squares in the rectangle represent 2 cookies.

I see 12 cookies. These 12 plus the 10 from the beginning equals 22 cookies in total that Dad baked.

Problem: A class has 5/9 girls. If the number of boys were doubled and 12 girls were added, there would be an equal number of boys and girls. How many students were in the class at the outset?

Naturally, I see this rectangle.

Then I do what the problem says.

The 5 pink boxes equal the 5 white boxes, so I cancel them out, leaving me with this.

At the outset there were 9 boxes, each box worth 4 students, so the answer is there were 36 students in the class.

So this is how I teach it to my students too. No equations. I remember a few years back one of my 6th graders' tutors was not happy with me that I'd assigned a PS involving "systems of equations." He said it was an algebra topic and how was a 6th grader supposed to solve it except for using guess-and-check. Really? Stuff people say that makes me fart.

Anyway, I've always looked at a square as two interlocking staircases, each a sum of consecutive integers. I also see a non-square rectangle as two interlocking staircases, one is the sum of consecutive odds and the other sum of consecutive evens.

12/7/12 12/7/12

Sharing My Favorite Math Books With Students

In my next life I hope to be able to collect pretty shoes the way I'm collecting math books in this life. Of course I haven't read them all. Not even close. But just seeing them on the bookshelf makes me happy.

A good book is nothing if not shared.

I always share some of my favorite math books with students. I bring them in for the kids to see the cover, the thinness of it, the fatness of it. Here's what the author looks like. Let's pronounce the author's name correctly. I read the book jackets to them. I tell them the year it got published — how many editions thus far. We look at the illustrations and say ooh-ahh-wow. I share some of the reviews.

I read at least one or two passages from the book. No matter how old the students are, they love this. They say, "Ooh, goody, story time!" Their eyes are on me. They "curl up" in their hard chairs. They want me to begin.

The latest book is Steven Strogatz's The Joy of X. I read the first paragraphs of "Loves Me, Loves Me Not" (Chapter 20) to my 8th grade geometry class.

"In the spring," wrote Tennyson, "a young man's fancy lightly turns to thoughts of love." Alas, his would-be partner has thoughts of her own — and the interplay between them can lead to the tumultuous ups and downs that make new love so thrilling, and so painful. To explain these swings, many lovelorn souls have sought answers in drink; others have turned to poetry. We'll consult calculus
....
To illustrate the approach, suppose Romeo is in love with Juliet but that, in our version of the story, Juliet is a fickle lover. The more Romeo loves her, the more she wants to run away and hide. But when he takes the hint and backs off, she begins to find him strangely attractive. He, however, tends to mirror her: he warms up when she loves him and cools down when she hates him.

I show them the love-hate-relative-to-time graph that follows. Then I say, "Take calculus in high school so you can plot your own Romeo-Juliet graph." I have them do a construction from Chapter 13, "Something from Nothing." Given a segment or one side of a triangle, construct the other two sides to form an equilateral triangle.

I admit I tend to favor pieces of work that show thoughtful struggle.

All I have to do is read Chapter 0, "Null and Void," in Charles Seife's marvelous little book Zero: The Biography of a Dangerous Idea and the kids are hooked.

Zero hit the USS Yorktown like a torpedo.On September 21, 1997, while cruising off the coast of Virginia, the billion-dollar missile cruiser shuddered to a halt. Yorktown was dead in the water.Warships are designed to withstand the strike of a torpedo or the blast of a mine. Though it was armored against weapons, nobody had thought to defend the Yorktown from zero. It was a grave mistake....Zero was at the heart of the battle between East and West. Zero was at the center of the struggle between religion and science. Zero became the language of nature and the most important tool in mathematics. And the most profound problems in physics — the dark core of a black hole and the brilliant flash of the big bang — are struggles to defeat zero.... Instead, zero shaped humanity's view of the universe — and of God.

My kids remember this when they see a zero in the denominator.

Amir D. Aczel's Fermat's Last Theorem makes me cry because it's so joyous and triumphant. Learning of the necessary interplay of mathematicians and their conjectures and discoveries to solve this 300-year-old math problem leaves me suspended in awe. I give the kids a quick recount of the story, then I read to them this passage near the end of the book.

Wiles walked around the department for several hours. He didn't know whether he was awake or dreaming. Every once in a while, he would return to his desk to see if his fantastic finding was still there — and it was. He went home. He had to sleep on it — maybe in the morning he would find some flaw in this new argument. A year of pressure from the entire world, a year of one frustrated attempt after another had shaken Wiles' confidence. He came back to his desk this morning, and the incredible gem he had found the day before was still there, waiting for him.

We also watched a video on Andrew Wiles — it was our Day 17 in geometry.

A delightful picture book that I read cover-to-cover to my 6th graders is Math Curse by John Scieszka, illustrated by Lane Smith. After reading the story, our class makes our own Math Curse book! Each student contributes one page to the book by writing and illustrating about a day in their life.

These are the covers of 3 books that the kids made from 3 different years.

And these are some pages within the books.

We didn't always make these books. Years ago we did Math Curse instead. I adore their Math Curse stories and have saved them since 2006.

Okay, I'll stop with these 4 books for now. Have you shared a favorite math book with your students lately? Sue shares hers here.

12/4/12 12/4/12

Parallel and Perpendicular Lines

Bleh. I don't know of a clever way to teach parallel and perpendicular lines. I'll try asking kids questions and maybe their answers will guide me and make me look smart until 2:50 p.m.

Me: Using your arms, show me parallel lines.

They do. One boy clasps his hands together like he's praying.

M: What do you know about parallel lines?
Students: They don't touch. They don't intersect. They don't meet.
M: Okay. Please draw this line in your journal. We're all drawing the same line, so make sure yours also passes through the points (0,-2) and (4,0)... Now, draw another line that runs parallel to the first.

I walk around the room and see that most of them have drawn pretty good "parallel" lines, not perfect.

M: How are you going to convince me that you drew parallel lines?

No one is talking. One kid has his hand up, but he's repeating algebra this year, so I ignore him. Poor kid is used to me ignoring him. His mother is adorable — and a friend of mine — and she ignores him sometimes too. Finally...

S: Check the lines?
M: What do you mean? How?
S: Extend the lines to see if they'll meet.
M: Extend until...? China? Where are we going?
S: The lines never meet!
M: So how do I check that? I need a way to check for parallelity. You say they never meet. Never, like infinitely-never-kind-of-never? I don't know how to check these infinitely long lines.

I'm stalling here. Say something smart, kids, so your clueless teacher can learn. I put my arms out, moving them together across my head like I'm doing a rain dance.

S: Measure the angle. Find the slope. Use a ruler.
M: Okay, let's find the slope because we know how to do this! So, find the slope of both lines. Don't talk to me again until you're done.
Jonathan: You can't die, Mrs. Nguyen. The Ducks would have one less fan.
M: I said don't talk to me. What are you talking about? Who's gonna die?
J: Remember you said that at the beginning of the year that if the Ducks lost a game, you'd die?
M: I do love you, Jonathan. Now, be quiet. Find slopes.

Jonathan draws the Duck mascot for me often, on his homework, corner of his test, on the big whiteboard. He also interjects random comments regularly.

The kids start talking, their heads nodding one by one, and they make this bold claim that parallel lines have the same slope. They say, "Let's do it again!" So we do it again. And again. After drawing three sets of parallel lines and finding their slopes, they tell me that parallel lines have the same slope. Hmmm.

They seem happy and gullible at this point. Best time to take advantage of them.

M: Show me your arms again. Wave them. Twist your hands like this. Do this... then this...

These kids kill me. So damn funny. They are like monkeys, doing everything I'm asking.

M: Okay, using your arms, show me perpendicular lines.

Yikes!!!!! Maybe, just maybe a fourth them show me arms crossed at right angles. The rest of them have no arm muscles.

M: What are perpendicular lines?
S: They cross. They intersect. They cross at right angles. Like an X.

So I put my arms up, crossing them like an X, but intentionally nowhere near ninety degrees.

M: Like this?
S: More straight. Like this. Yeah, that's it!
M: I heard right angles. Is that true?
S: Yes.
M: Draw me another line, please. This one going through (-2,0) and (2,1). Then, I need you to draw, as best as you can, a line running perpendicular to it.

Holy cow. Even the kids who say the words "right angles" and "ninety degrees" draw nothing near that. But one student, after I look at five others', does have a good sketch, so I show it to the class.

M: C'mon now. Please try again. Then what should you do after that?
S: Find their slopes!

Here's one student's attempt at drawing perpendicular lines. But you can see her second attempt is better.

(The first line has a slope of 1/4.) Unfortunately the kids who do have a decent looking "perpendicular" line find the slope to be 4 when it should be -4. Again, we do a total of three sets of these. They describe the two slopes: opposites, inverses, flip around, reciprocal, upside down. I don't really care what they call the relationship right now because when I give them a line having a slope of 3/7, they know the slope of a line perpendicular to it is -7/3. They know when one is -8, the other is 1/8.

Everyone draws the same original line together. But instead of trying to draw the perpendicular line to this (like we did on that first round) — a difficult task to perfect via eyeballing — and then find the slopes of both, I ask them to find the slope of the original line first, then find the perpendicular slope, then use this fact to draw in the second line. They think it's cool that they can start the second line using any point on the coordinate plane.

I'm saved by the bell. And I think know this is still better than my just telling them.

10/11/12 10/11/12

Mr. Meyer's Taco Cart

Won't be long before I have to change the post title to Dr. Meyer's Taco Cart. This lesson went really well today.

Act 1: We watched the video clip. Their guesses:

Me: That was fun. Kinda split in the middle there with your guesses. But that question of who gets there first only gave you two choices, Dan or Ben. What other fun questions could we ask?
Student 1: The length of the road.
Me: I did say "fun."
Student 2: What their walking rates are?
Me: That's funner than "length of the road"?
Nathan: What is the fastest route?
Me: What do you mean by that? Can you come up and show the class what you meant?

Nathan came up and traced out the blue path with his finger, "They can walk to the cart like this..."

Me: Oh, okay, what is the fastest route? Yeah, right, because what if neither of the guys' routes was the fastest? This will give us a bunch of different guesses. Or, a similar question, where on the road should Dan or Ben enter to reach the taco in the shortest amount of time?

I gave each student this working placemat (Dan's Act 2 slide) for work space and the road strips to throw down a guess. They needed to line up road-on-paper perfectly with road-on-strip before marking their guess so that both marks indicated the same position.

Their guesses:

Act 2: The questions began.

Me: Okay, so now figure out how much time it takes to walk the route that YOU chose.
Student: Can we have the dimensions?
Me: Which one?
Student: All of them.
Me: Wrong answer. Try again.

They yelled out for the legs, the sides, the road, the hypotenuse.

Me: I'm just gonna give you one of the sides. Just one. Ask wisely.

For whatever reason, they agreed it should be the hypotenuse. (Dan did not give the length of the hypotenuse on his slide. I purposely put a white box there pretending like maybe they could ask for this length too.)

I gave them the hypotenuse as 650.0 feet. They stared back at me, faces scrunched up as if they were begging. They knew they needed another length to use their trusty little equation of a^2 +b^2 = c^2. I also gave them the walking rates on sand and on road.I walked around the room, peeking to see what they were doing on their papers. One student plugged the rates into the equation. He wrote this:

The 2 and 5 in the bottom equation came from the walking rates. The 105625 seemed to have come from multiplying the distance (650 feet) by the time to walk that distance on sand (325 seconds), then dividing this number by 2.

Half of them were just quiet — daydreaming, thinking.

Almost 10 minutes had passed. I said, "I gave you the hypotenuse, correct? But before I gave you the hypotenuse, don't you have the hypotenuse on your paper?"

Five seconds went by, then...

Gabe: Proportions!
Lauren: O my God, I hate that when I think too hard!
Nathan: I thought about measuring!
Janelly: Me too! But I was afraid to.
Maia: Do you measure with a ruler?
Janelly: No. Measure with your toe.

Ha!! Measure with your toe!! How can I not love these kids. So, they got busy with their rulers.

Maia: Should we measure in inches or in centimeters?
Someone: Centimeters! We never measure in inches in here.
Me: Not never. But why might we want to measure in centimeters for this problem?
Someone else: It'll be more accurate.

They measured carefully and checked each other's proportions. And because I only gave them the hypotenuse, their calculations for the legs weren't all the same, but close enough. We respected the margin of error when using a ruler.

It was another day that I didn't want this class to end. But with only five minutes left, I had to wrap up the lesson.

Me: What's the chance that your guess happened to be the fastest route?
Various students: Not likely. Way off. I think mine is perfect — I picked exactly half-way on the road. More to the left, I think.
Me: So, after you figure out the time for your route tonight, I want you to pick another point on the road. Do two sets of calculations.
Nicole: Like do it again for a different location?
Me: Yes. And if you chose your second point to be on the left of your original guess, then why? Or to the right, why?
Thomas: Will you tell us who got closest tomorrow?
Me: Sure. I have your original guesses already [on the strips]. And guess what? The student with the closest answer gets a Del Taco lunch!
Students: Really? What about Taco Bell? I love tacos! I hope mine is closest! Are we taking a field trip there?
Me: Fine. Taco Bell or Del Taco, your choice.

Act 3: We'll have to wait until tomorrow to see everyone's work and answers for their chosen paths. I'll reveal this again with the green line drawn in to indicate the best spot to enter the road. But it would be so cool to get some numbers right near the minimum time. Maybe I'll bring up differentiation. Maybe we'll plug something into Wolfram Alpha.

What made this lesson work for my kids:

Nathan's question of "what is the fastest route?" allowed for a lot of entry points than just "who would get there first, Dan or Ben?"
Giving them just one side of the triangle was really the best thing I did for this group of kids. Because once they figured out the other legs, they just tapped away on their calculators — already comfortable with the equations they've worked with before.
The strips provided me with an easy way to display student guesses.
Printing out Dan's Act-2 slide as work placemats for students allowed uniform access to the beach scene and made measuring the triangle sides possible.
I only thought to ask the kids to pick another point to figure out for homework just seconds before. Glad I did because we just doubled our data points!
The promise of Del Taco. No, I can't just give to the kid with the closest answer. I'll make sure I bring in enough for the class. This fun lesson deserves a fun closing.

Thank you, Dan.

Updated 11/07/12

10/6/12 10/6/12

Using Excel for Problem Solving

One of the more enduring lessons that I do with my algebra class is having them use Excel for problem solving. Don't know why I haven't written about it as I've been teaching this strategy for at least 5 years now. (I don't recall reading other teachers' blogs about using Excel this way either.)

Hand-Holding

I pose this familiar — 5th grade? — problem to my 8th graders.

There are 53 horses and cows in Farmer John’s farmyard. There are 21 more cows than horses. How many of each type of animal are there?

I let them work on it for a few minutes. Most will share that they use guess-and-check. Then I just have them watch and listen as I solve it via Excel. After that, they grab their laptops, along with this printed instruction, and try to repeat the process. The problem is intentionally easy so they can just focus on entering information and simple equations into the cells — get acquainted or reacquainted with spreadsheets.

You Try

Then I give them this problem to try on their own.

For a play, the ticket prices were $5.00 per child and $8.50 per adult. The children bought 100 more tickets than the adults. The total box office income was $905.00. How many tickets of each type were sold?

I let them struggle on this and encourage them to help each other. About 10 minutes later, I step in to guide them by asking lots of questions. We arrive at one possible way to set this up in Excel. (I hid rows 8 through 25.)

Have Fun

I give them this set of 16 Excel problems and ask them to choose just 3 or 4 to work on.

Extension

It's also great to use Excel to solve problems like Daniel and the Devil.

The devil made a proposition to Daniel. The devil proposed paying Daniel for services in the following way:
"On the first day, I will pay you $1,000 early in the morning. At the end of the day, you must pay me a commission of $100. At the end of the day, we will both determine your next day's salary and my commission. I will double what you have at the end of the day, but you must double the amount that you pay me. Will you work for me for a month?"

Or Salary Plans

You just got a job at Jimmy's Skateboard Shop. You have a choice of two different salary plans.
Plan A Earnings: $120 per week plus 10% of sales
Plan B Earnings: $90 per week plus 15% of sales
You can expect your average sales per week to be $400. Which salary plan is better?
For most retailers, the months of November and December bring in a lot more sales than usual. Say you can expect your sales per week to be $1,000 during these two months, then how would this influence your decision on which salary plan to go with?

I love it when my kids ask if they may use Excel to solve problems, especially when we get to systems of equations. Yeah, one more strategy in their toolbox!

10/3/12 10/3/12

Foxy Fives - Cuz It’s Better Than Four Fours

Foxy Fives is my Day 21 lesson (actually a game) that I got from this book. The teacher is supposed to make a deck of 62 cards from posterboard, the cards are marked from 1 to 25, and blah, blah, blah. For the life of me, I don't know why you'd need a deck of cards at all to "play" this game because the instruction TELLS YOU to deal yourself a specific set of cards for each round, like cards numbered 1, 5, 3, 6, and 10. There, I just dealt myself a hand.

Other than that ridiculousness, it's actually a great lesson for students to apply the order of operations to a set of numbers.The game has three sheets. And just for you, I'd completely retyped them to remove the silly language about dealing out cards. Here are Foxy Fives Sheet 1 and Foxy Fives Sheet 2 — I save these for my 6th graders.

The 8th graders get this more challenging (thus, more fun) Foxy Fives Sheet 3.

I had kids work in groups of three on the large whiteboards.

You can tell from Sheet 3 that it's asking the kids for more. It's great to do this after we just discussed number systems. The kids struggled and struggled. (Quite a lovely thing to bear witness to.) Most groups found a couple. One group found the first five!

Also, I was very clear about them reporting their answers like this:

And NOT like this:

My next plan is to put each of the 10 questions onto a large poster paper and put these up around the room. I will encourage kids to contribute their solutions to each problem over time. It's good for them to see that there are many solutions possible. And, they can also check others' work for correctness! Such a nguyen-nguyen if I ever saw one. (When I left a local high school position, the students' newspaper did a story on me, they titled it, "Students Find Themselves In a No Nguyen Situation." So cute.)