My Other Math Sites
Lessons From the Classroom
Hotel Snap
[NCTM Illuminations has my blessings and thanks to re-write and feature this lesson on their site.]
Andrew Stadel and I recently presented this task at the 2013 CMC's North and South Conferences.
The Challenge
As a team, build a hotel that yields the highest profit [score].
Rules and guidelines for building the hotel
Each cube represents a hotel room. All 50 cubes must be used.
Hotel must stand freely on at least one side of cube. Here’s a non-example because it’s tilted.
Entire hotel is one piece. A non-example due to yellow cube not attached:
All rooms must have at least one window, a window is any exposed vertical side of cube. The white cube below has no window.
Building costs and tax (daily rate)
Land costs $400 per square unit.
Land refers to outline of top view of building.
All enclosed land is charged, for example, squares marked 8, 9, 10, and 11 in the left outline are open space, but because there's no access to the outside, you are charged for these 4 square units.
A roof costs $10 each, roof is any exposed top side of cube.
A window costs $5 each.
Tax on height of building is calculated by multiplying the tax rate for the highest floor by the total land cost.
Floors 1-10 —> 50%
Floors 11-20 —> 1000%
Floors 21-30 —> 2000%
Floors 31-40 —> 3000%
Floors 41-50 —> 5000%
Income from each type of room (daily rate)
The more windows, the more income.
4 windows, 1 roof = $600
4 windows, 0 roof = $500
3 windows, 1 roof = $300
3 windows, 0 roof = $250
2 windows, 1 roof = $200
2 windows, 0 roof = $175
1 window, 1 roof = $150
1 window, 0 roof = $125
Scoring
Your net profit/loss income will be checked for accuracy. A deduction of 50% of your error will be applied to the actual number. For example, your building nets a profit of $13,500, but your group submits a profit of $15,000, therefore you're off by $1,500. Then 50% of this error ($750) will be deducted from the $13,500 to give your team a score of $12,750.
If your calculations are right on, then your team's score will be awarded an extra $1,000.
Adapting this lesson
Change the number of cubes, as few as 10-15 cubes for younger kids, and maybe up to 100 cubes for high school students.
Also for younger kids, have the Excel file (more on this later) readily available on computers so kids can go back and forth between checking their profit margin and tweaking their hotel rooms — so no calculations needed on their part, they just need to be able to know how to count the different types of rooms.
Older students can create the spreadsheet, it's great practice for understanding how cells work and formulating equations.
Adjust the time for individual and group work based on your expectations.
Modify, take away, or add to the rules and guidelines.
Change any of the costs/income/tax numbers.
Change how you reward accuracy or penalize mistakes.
Ask each group to estimate and rank the profit margins of other teams' hotels just by looking at them (like on a -5 to +5 scale, -5 for biggest loss and +5 for biggest profit).
Ask, "What if all costs and tax stay the same, but now the incomes for the rooms are all reversed so that 4-window-1-roof earns only $125 while 1-window-0-roof earns $600? How would you build your hotel using the same rules?"
If I were to do this with my 6th graders, I'd first have everyone build the same 10-cube hotel with me, then we'd use this hotel to familiarize ourselves with the different types of rooms and tally them up. We could calculate the costs and income together for practice.
How I ran the lesson with 8th graders
(I did this lesson with two classes of 8th graders, one geometry and one algebra. We have 57-minute periods. This lesson took 2.5 periods. I'm so scripted here because the one thing that kids wished they had more of was time. Your teacher instruction needs to be tight and supplies distribution needs to be efficient to allow for all the student work time needed.)
State the challenge of task.
State the rules/guidelines.
Give each student a zip bag with 50 cubes — but I first took time to show them that how they see the cubes now is how they need to be put away when we clean up.
Give each student this cost_income_sheet:
Set timer for 15 minutes for individual work, reminding students that later they will be randomly assigned into groups of 3 to work on one hotel.
While students are working, I use Instant Classroom to put kids into groups of 3.
When the timer goes off, I give the following instructions:
I now need you to listen to directions for working with your teammates, and when I'm done giving these instructions, I will set the timer for 25 minutes for you to work. During this time, you'll need to do the following:
Share and discuss the best model to represent your team's hotel.
You may modify this chosen hotel, or you can even start from scratch, but watch your time.
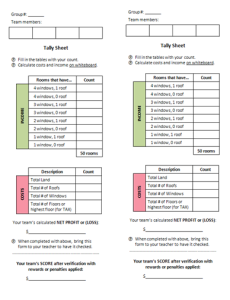
Use this tally_sheet to record your room counts, land, roofs, etc. — remember this is just a tally sheet, so you want to do all your calculations on whiteboard.
On the large whiteboard, divide it into 4 quadrants, and your group will need to fill in 3 of the 4 quadrants answering these questions. Watch your time carefully because when the timer goes off, the hotel you have in front of you is the one you must keep as is.
Allow a couple of minutes for groups to get supplies and settle down together with their individual hotel models. One tally sheet needs to be passed out to each group.
Timer is set for 25 minutes. Monitor the groups, check for understanding, and listen in for building strategies. Keep counting down the time every 5 minutes.
When timer goes off, ask groups to break down the hotels that were not selected and put the cubes neatly back into the zip bags and return to the front.
Next day...
Kids get back into their groups with their whiteboard and hotel. Some groups may still need to finish filling in their tally sheets and whiteboards.
The question for the 4th quadrant is now asked: "If you could relocate just 5 cubes on your hotel, where would you place them?" Remember that you are no longer allowed to change your hotel, this question is just a what-if scenario.
Allow 10 minutes for groups to finish filling in their tally sheets and answer all 4 questions on whiteboard.
As indicated on bottom of tally sheet, groups are asked to bring up the tally sheets to teacher to check their calculations and arrive at the final score.
The Excel sheet
I have two files: one locked and one unlocked. The "locked" one so of course no one can inadvertently change the cells, especially wise if you give kids access to the file to use on their own - only the blue cells to enter data are open. The "unlocked" file is so you can edit as you please.
Notice that all the cells appear in the same order as the tally sheet, makes for quick entries with instant results. My husband gets most of the credit for this, I still claim credit for making it simpler.
Math Practices
I found this form 8_MP_questions_to_ask online and can't find it again to cite the source.
I'm making good use of this form after almost every task now. Students do this for homework. I ask them to highlight the questions that came up during the activity - from teacher, peers, and self.
We discuss this as a whole class the next day and generally come to a consensus of which math practices our task had fostered.
Reflections
We presented this lesson because it went really well in the classroom. The kids were completely engaged. They collaborated, talked a lot among themselves about what they were building and thinking, but they were pretty much dead silent during the initial individual work time. I love seeing the structural varieties — this was true too among the hotels built by math teachers.
To not spoil the fun, I won't post pictures of the high-profit hotels here, but I'd love to learn what some of your profit numbers are from your class.
Last Math Lessons
On the first day of school, I promised all my students that I'd do my best to make math relevant and challenging. I also promised to never waste their time, therefore they could expect to do math every day in my class, including the last day of class.
I did not promise them that math would be fun because doing math is always fun to me. I gave out math puzzles at my kids' birthday parties when they were younger, also at a baby shower that I gave, and of course at my own wedding.
Math 6
I called this lesson How Many Regions? (Adapted from AIMS)
I gave each student a piece of 4-by-4-inch paper and a handful of 6-inch long thin strips of construction paper. Each strip placed on the square paper would represent a "cut."
Question: What is the maximum number of regions that you can divide the square into using n number of "cuts"?
We did the first two cuts together as a class, and each student kept track of the data in their journal.
Because the goal was to get the maximum number of regions from the cuts, the kids learned quickly that the cuts needed to intersect. For example, two non-intersecting cuts created only 3 regions. A kid yelled out, "Parallel cuts!" Gotta forgive kids who blurt out academic language!
This class has been working with a pattern worksheet almost every Monday in my class, so they know to look for a recursive rule and try to find the equation for the nth term. Recursively, they saw the pattern, so it didn't take long for them to figure out that for any n (cuts), the maximum number of regions is the sum of n and the number of regions from the previous n.
With 30 seconds left of class, I told them my gift to them was to try and figure out the equation. Matt asked, "Can I email you then over the summer?"
Algebra 1
Our 8th graders' last day of classes was yesterday (Wednesday). They'll show up this evening for their promotional ceremony, dressed to the hilt.
I needed a quick one-period lesson, so I had them make 2012 Clocks. This is a common assignment: using all 4 digits in "2012" and each digit only once, they had to create expressions that would equal to the hours of 1 through 12 on a clock.
Geometry
I've seen different versions of this problem; the first time I worked on it was when it involved 3,000 bananas and 1 camel traveling 1,000 miles. I know there's a perfectly good strategy called "solve a simpler problem," but we could also start with a simpler one!
I gave my kids Desert Crossing, also from AIMS:
You live in a desert oasis and grow miniature watermelons that are worth a great deal of money, if you can get them to the market 15 kilometers away across the desert. Your harvest this year is 45 melons, but you have no way to get them to the market, except to carry them across the desert. You have a backpack that holds up to 15 melons, the maximum number that you can carry at a time. To walk across the desert, you need a certain amount of fluid and nourishment that is supplied by the melons you carry. For each kilometer you walk (in either direction), one melon must be eaten.Your challenge is to find a way to get as many melons as possible to market.
As I type this, Slater does not know that I will be awarding him the Math Excellence Award at the Promotional Ceremony this evening.
Here is Slater's work that shows one way to get the correct answer of 8 watermelons.
I did this a few weeks ago and forgot all about it; so here's a little blurb on it.Each student quickly constructed these two prisms from two same size papers.
(Dan Meyer folded them into cylinders.)
Question: Pretend the two prisms have bottoms on them, which one holds more popcorn? Take a look... Okay, grab the one you think holds more, or grab both if you think they're both equal.
And this was how they grabbed:
Then they measured and calculated the volume.
My favorite student comment: The tallness didn't make up for the fatness.
Estimating volume is a funny thing.
Visualizing Volume is Tricky!
This was one of those lessons that I think I gained a lot more than my 6th graders did. It was meant as a one-period activity, but I kept going off on different tangents and brought the students along for the ride.
Over a month ago Andrew Stadel tweeted me a picture that he took of a William Sonoma display of their cupcake mixes. I was at our local mall last Sunday and saw a similar display. We both thought about buying the mixes to make cupcakes for our kids, but it was $15 a can, and we'd need three, so the poor teachers said no can do.
I projected the images above and asked the kids to give me a guess of how many dozens or how many individual cupcakes can the large container make when the small [real] container can make 1 dozen or 12 cupcakes.
Their guesses were all over the place, ranging from 47 to 994 cupcakes. (We were very careful whether the submitted guesses were in "dozens"or in "individual cupcakes.")
So I did the only thing I knew. I replicated the two cans so the kids could see them physically in the room instead of just on a still photo. Granted the large "can" made from butcher paper was pretty awful.
But, before I asked for another guess at the number of cupcakes, it occurred to me that I wanted to know if kids were better at guessing one and two-dimensional items.
Question 1: How many times taller is one segment than the other?
The two segments below are proportional to the heights of the two cans.
Their estimates:
Question 2: How many times longer is one circumference than the other?
The two circles are proportional to the cans' tops/bottoms.
Their estimates:
Question 3: How many times larger is the area of one circle than the other?
The two circles are proportional to the cans' tops/bottoms.
Their estimates:
Then, I let the kids — row by row — come up to get a visual check at the paper replicas of the cans. But they may not manipulate the models because I was more interested in seeing the difference between their guesses of the still photo and the physical models.
Their estimates:
If I wrote this post as Dan's 3-Act Lesson, then it was time for Act 2: figure out the volumes of the two cans using their measurements. (Yes, I carry a measuring tape wherever I go now.)
I tried to show the kids equivalent measures whenever possible. We worked a lot with centimeter cubes this year, so this was a rare time that we measured in cubic inches.
And here are some estimates from grown-ups who only saw the left image at the top of post:
(Got more guesses after I printed this: 1,000, 182, 600, 576.)
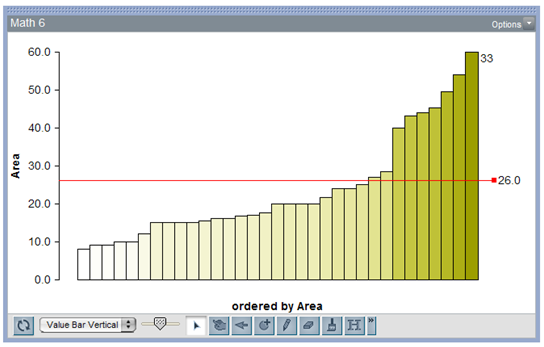
The straight lines [heights] seemed easiest to estimate. It got a little bit tougher when these lines bend into circles [circumferences] — and there was a large number of over-estimates here. I thought area estimates were pretty good, average of all 33 student guesses was 28.3 (calculated was 26).
The volume estimates, from kids and adults, remained well under the calculated numbers. I don't know what to make of all this. But I kept wondering: Are boys or girls better at making volume estimates? (From my small sample of 33 students, the girls were closer.) How about science teachers? The 3D models helped overall; and I bet if I let the kids do everything but measure the cans, their numbers would be closer. Interestingly, at one point I'd placed the smaller can inside the larger can, and kids who stood nearby kinda gasped. One said, "Oh, you can fit a lot inside."
Thank you, once again, to Andrew for sending me that tweet that started all this! He did a wonderful presentation of 3-Act Lessons to his staff.
Designing Buildings
The idea for this lesson is from Measurement in the Middle Grades, published by NCTM in 1994. It's still available here. I created this worksheet.
I purposely did not give the kids interlocking cubes to complete question 1 — wanted to see if they could count the number of windows and rooms from just the diagrams. A few students had some trouble counting the number of "windows" in Buildings D and F.
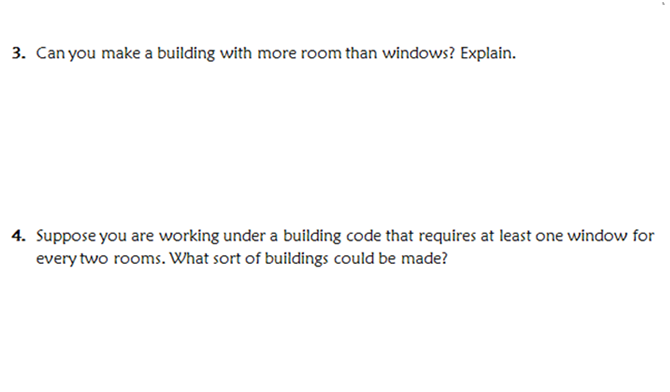
In question 2 below, students needed to create three buildings, each with a specified number of rooms and windows. I passed out interlocking cubes and isometric dot papers at this time.
While some kids could create a building, they have a tougher time drawing it on dot paper. Rapha had a suggestion for us.
Matt built this and wanted to know if it could be considered a "building." The class redefined it as "It's a building if it can stand without tipping over."
But before they attempted to draw the buildings, I asked them to give their building to at least one classmate to see if he/she would get the correct number of rooms and windows. They were very engaged to construct the buildings and draw them to complete question 2.
We were into our second day on this. At least half of the kids were now working on questions 3 and 4.
And these were some of the answers for questions 3 and 4.
They were very much into the building and drawing, so I went around to ask them what they thought of this lesson thus far:
It lets me be creative by drawing and making, see how it comes out.
It's difficult to count the windows. I check with my classmate and it's wrong!
This is awesome fun, question 4 is challenging, I'm still trying to figure it out.I'm stuck on creating Building 3, it's difficult, but I'm pretty close.
I like the different ways that I can build.
I never thought question 3 would make me think so hard like this!
Drawing is easy for me, it's more difficult to build.
The 3-D drawing got easier after Rapha helped me.
It's difficult. It's not working out (referring to creating Building 2), but it's fun to try to find it.
Very fun, I like it because I can help people with it, show them how to draw perspective.
My conversation with Sam about his paper:
Me: Help me read your answer to question 4.
Sam read it and added: Imagine a gigantic cube building... Well, all those rooms on the inside don't have windows. So, no passing the code!
Me: How big is gigantic? What size?
Sam: Hmmm... 25 cubes on each side?
Me: Okay, like 25 by 25 by 25.
Sam: Let me get a calculator.
Class was ending. I asked the students to finish this for homework. I let a few students take some cubes home because they asked. I look forward to Sam's calculations of rooms and windows for his "gigantic" cube. I look forward to our class discussion tomorrow — I've never heard both words "fun" and "difficult" to describe a lesson as often as I'd heard it here in this lesson.
Why Wait for Calculus?
(I just had my very best lesson yesterday, on a Friday, thank you. I feel almost brilliant right now. And I only feel like this once every 47 years, so please stay and read this post!)
My own kids tell me they will stock up their dorm rooms and apartments with junk food and soda when they move out to make up for these years of deprivation. (And this is supposed to make me feel bad.) So when I intentionally bring home a snack, like this bag of kettle corn, I usually find it empty within 24 hours. But seeing the empty bag made me think of a volume activity that I could do with my 6th graders with all these other bags of Orville Redenbacher's popcorn.
But the activity I had in mind — maximizing the volume of a box — is commonly done in a pre-calc or calculus class. These are my 6th grade babies. But didn't we do okay with approximating the volume of a torus via my doughnut lesson? So, why can't we do this too? I have to get rid of the popcorn.
I randomly assigned the kids in pairs, gave each pair two sheets of white copy paper. I told them to use one paper at a time to make a box — the goal is to make the box as big as possible so it'll hold the most popcorn. But the box must be made simply like this: cut off 4 corners from the the paper, then fold up the sides and tape them together. I used a half-sheet (so they couldn't duplicate mine) to demonstrate what I meant.
They quickly went to work. A few students were NOT cutting off square corners, so the top edges of the sides didn't line up. Two groups folded in their papers, in addition to cutting off corners, so they had to re-do.
Ryan and Annamaria wanted to make a shallow box. Ryan said, "... it doesn't matter how high it is."
Rapha and Cristian made the biggest corner cuts that I saw in the first round.
Mike's and Roy's first box was the shallowest in the class, but they changed their mind for their second box.
With 10 minutes left in our first hour together, I asked the kids to measure the box and find the volume. They had no trouble with this since we did the doughnut. They recorded the volume inside each box, and I tacked them on the board. (The butter seeped through in few of the boxes.)
Well, that was fun. I pointed out that two of the bigger boxes were over 1,000 cubic centimeters. The bell rang. I said, "We'll wrap up this afternoon."
I didn't know what I was going to do to "wrap up" the lesson. The microwave actually overheated — my room stank of greasy popcorn.
There was a confidence in me, however, that the kids would help me figure out how/where this lesson could go next. I began the afternoon hour by going over what they'd learned in the morning. They said:
The four corners must be of the same size. (I never told them this in my instruction.)
Each corner must be a square. (I didn't tell them this either. Not everyone was convinced of this, so I cut non-square corners to show them.)
There was a limit to how big the square could be. (I loved this! And this made me ask, "Is there a minimum to the size of the square?" Their eyes squinted, almost as if they were trying to "see" how small these corner squares could get. One kid said, "No. Technically, no.")
The volume numbers that people wrote down could be wrong.
By then they understood the different boxes and their volumes depended on the size of the corner squares that would get cut off. We focused on this. I asked them to draw a 10 x 12 rectangle in their math journal. We removed 1 x 1 corners from this rectangle and found the volume. I guided them through the next 2 x 2 corners. They continued on their own.
Then I gave each kid another white piece of copy paper. We measured the length and width of the paper and agreed that the paper was 28 cm x 21.5 cm. I asked them to build a systematic table like the one they just did in their journal. I said something like this, "Because you now know how to figure out the volume without actually cutting and making the boxes, see if you could figure out what size square the corners should be to maximize volume."
I saw kids high-fiving each other, "The corner has to be 4 by 4!" Rapha and Cristian beamed after congratulating each other, "That was one of the boxes we made!" We ended class with that. I swore I felt myself tearing up.
On Monday we'll play around with this applet.
And we'll ask Wolfram Alpha to take the first derivative of the volume for us. (I'm pretty sure the class could write this equation V = (28-2x)(21.5-2x)(x) for me to enter into WA.) Well, I actually just did it, and WA gives the side of our corner square as approximately 4.01965. My kids got 4 — pretty damn good for 6th grade brute-force math. Now that I'm writing this, however, I am really most proud of how well the kids had worked together. I randomly paired them up — a handful of the pairs were like the odd couples: high/low, shy/outgoing, squirrelly/quiet, jock/nerd, princess/cowboy. There was not a whisper of whine when their names were called to pair up. How did I get so lucky?
I am a doughnut.
I cannot eat a doughnut without thinking of Eddie Izzard. Language caution in this video clip.
Ich bin ein Berliner aside, I needed a calorie-laden lesson for my 6th graders to welcome them back into the classroom after two beautiful spring break weeks.
(We are also two short weeks from state testing and should be reviewing for the test. But who wants to do that when one can eat a doughnut instead?!)
I got the idea for this lesson from NCTM.
Estimating Volume
I held up one doughnut and a centimeter cube and asked each student to write down an estimate of the doughnut's volume in cubic centimeters. But first, I needed to tap the kids' prior volume knowledge.
Me: So, what is volume? What is the volume of this doughnut?
Julia: Length times width times height.
Me: Hmm... Where is the length of this doughnut? Or its width?
Julia: Oh...
Matt: It's the inside of something.
Sam: But that's area.
Rapha: It's the whole thing. The doughnut itself.
Matt: No, I mean the space inside.
Julia: Oh... it's how many of those cubes fit inside the doughnut!
I always dread hearing kids give me a formula for anything unless I specifically asked for a "formula," but this time I didn't break into hives.
I asked if it would be okay that I just counted the centimeter cubes in each of the solids below to find volume. The kids immediately pointed out the empty space inside and one said, You have to add like 5 to your answer to make up for the space. Another student said, More like add 10.
The class agreed that the cylinder held more cubes than the sphere and that the doughnut would be bigger than the cylinder. I told them there were 69 green cubes in the cylinder and allowed them to change their doughnut volume estimate if they wanted to.
When a centimeter cube was placed on the doughnut box, almost everyone said, Wow! (This made me happy because it showed they thought of volume as volume, not length-times-width-times-height.) They recorded their estimates for the box's volume.
Estimating Surface Area
When I asked the kids about SA, they said the outside, all-around, total area, all the surfaces, and doughnut skin represented SA. I added that the amount of glaze could also represent SA.
I told them this grid paper had 22 by 18 rows or 396 square centimeters and asked for their estimate of the doughnut's surface area.
They also recorded their estimate of the box's surface area.
Measuring the Doughnut
To manage this potentially messy lesson, the doughnut had to stay on construction paper, and all measurements had to be taken with a paper ruler.
Students took as many different measurements of the doughnut as they thought necessary to figure out volume and surface area.
They ate the doughnuts, and Cristian wanted me to take a picture of him.
We'll wrap up the lesson tomorrow and discuss approximating for volume.
No, none of my 6th graders brought up any of these -us words: torus, annulus, calculus. However, we did a lot of estimating and measuring with visual and concrete models. We each gained 200 calories from this.
Updated 04/17/12
In my comment, I told @Peter_Price about making a cylinder similar to the doughnut; then, I found this roll of masking tape that was close in size!
My 6th graders are familiar with area, so surface area was easy to grasp. (I felt smart when I could just peel off the tape to show the side SA.) I showed them my set of vinyl nets to the geo solids also.
I needed the students to figure out how to calculate volume on their own. I used these two models because of both the CDs and the patty paper sheets are very thin.
Student A: Find the area of one sheet and multiply by how many sheets there are.
Me: There are 1,000 sheets here, so area times 1,000 gives me volume?
Student B: No, that just gives you the area of 1,000 sheets, kind of like their surface area, but you're still doing area, aren't you?
Me: It would seem so.
I told the class that finding the area of one sheet was correct. And they also knew that it was the same area as the base of the box. Then I poured out the stack of CDs and started filling its container back up one by one. (Easier than stuffing the patty sheets back in.) I said quietly. Volume is three-dimensional.
The class watched, and soon, the hands went up. Before I could call on anyone, a few students couldn't contain themselves and violated our classroom rule of waiting to be called on before talking. Two kids yelled out, The height! Then more chimed in to say, Multiply by the height!