My Other Math Sites
Lessons From the Classroom
Number Talks for Middle Schoolers
If I may recommend only one thing to K-12 classrooms, that thing has to be number talks. As a warm-up routine, it usually takes less than 10 minutes, yet it pays dividends in building number sense, connecting computational strategies, honoring flexible thinking.
I finally finished this set of 90 number talks for middle schoolers — enough for a full school year if you do this routine every other day. But I hope you’ll also share it with your elementary and high school teachers to inspire them to create their own or modify these.
I’ve already shared my notes about the routine on the first 4 slides. I just want to add that each slide — or each group of 3 slides — is intentional, meaning there are several strategies that I hope your students and you will explore and share. My goal is also to tweet these out, one at a time, and include people’s responses on a slide following it.
You know what you should do on the other 90 days. :)
Comparing Fractions
I was taught to find a common denominator when comparing or ordering fractions. Find the LCM. Even change them into decimals.
Instead, I want to compare fractions in these three ways:
Using number sense and the fraction 1/2
Finding a common numerator
Thinking of them as perfect pinks or not
Compare 3/4 and 5/12.
3/4 is more than 1/2, and 5/12 is less than 1/2, hence 3/4 > 5/12.
Compare 1/5 and 2/7.
1/5 is the same as 2/10, and 2/10 is smaller than 2/7 because pizza.
Compare 5/7 and 6/9.
A perfect pink color is made from 1 part red and 2 parts white, expressed as 1/2. I have a visual sense of this color, this red/white ratio of 1/2. Anything greater than 1/2 is dark pink, and anything less is light pink.
So 5/7 is darker, and to get to the color of 6/9, I’d need to do this: 5/7 + 1/2 = 6/9. If I’m adding something less dark than what I’d started with, then I’m going to dilute the color, so 6/9 is less dark than 5/7. I conclude 5/7 > 6/9.
Of course if I add the exact same color to itself, then there should be no change: 2/3 + 2/3 = 4/6.
Compare 19/60 and 21/55.
19/60 is light pink, so is 21/55. To get from 19 to 21, I’d need to add 2 reds, and to get from 60 to 55, I’d take away 5 whites. The net effect is more red, making 21/55 darker, or 19/60 < 21/55.
This is not unlike how batting averages work.
Reversing the Question
Don Steward posted this on Sunday. Like Don, I really like this task and also think it has a certain Malcolm Swan je ne sais quoi about it.
I showed only the top part to my 6th graders, and I gave them 2 minutes to write down what they noticed.
In addition to noticing the given information, the students also mentioned:
It takes a lot of grams to make a sponge cake.
A kilogram must have a lot of grams in it.
The unit of measurement is changed in the cake and in the big bag.
This problem doesn't have a question.
The sponge cake has no price.
There is frosting on the cake.
You need to change the measurements first (kg - g)
The cake weighs more.
The cake is really small and the flour is really big.
Not much information and there's no question.
There is no question.
The weight of the bag is in kg but the flour it takes for the cake is in g.
You have to convert 24 kg to grams.
It uses only very little of the flour.
I gave them another 2 minutes to write down what they wondered.
How much the sponge cake costs.
How many sponge cakes can you make.
How big is the sponge cake.
How to convert from kg to g.
If the sponge cake is good.
24 kg is <, =, or > 150 g.
What we are going to have to solve.
Is the question going to be about if there's enough flour or is it going to make us change it from kg to g.
How much 24 kilograms is in pounds.
How many grams are in a kilogram?
How many krumkakes can you make with the bag of flour.
How long will it take for the cake to be ready.
What a sponge cake is and what the recipe is for the cake.
How much flour is left.
What flavor is the cake. (Sorry. I'm hungry!)
What you're wondering that I'm wondering about.
What the question is, and if there are more ingredients.
If we will have to find the price for the sponge cake, or maybe we have to find out how much half as much flour is worth.
Then we moved on to next part of providing questions that would go with the calculations. This was so very tough for my kids. While 21 of 31 kids could come up with the correct question for part (a), they were lost with what to write for the other three parts.
Because we didn't care what the numerical answers were, the kids didn't do any calculations, instead they were supposed to focus on the operation(s) in each problem and decide on the question that would prompt a specific operation.
The most common question for part (b) was, "How much does 1 kg of flour cost?" (I'd swapped out £ for $.)
Then my next step would be for them to go ahead and use a calculator to get the numerical answers. They will see that for part (b), 24 divided by 21.50 equals approximately 1.12. And if 1.12 were the cost for 1 kg of flour, then 24 kg of flour should cost more than $24. But, wait. We already know that the bag of flour costs $21.50. Hopefully they'll arrive at this contradiction on their own, and re-think their question.
We'll then attach the units to the numbers accordingly and let the conversations continue. When kids tell me that they will calculate two numbers using operation w, I always follow up with, What does your answer mean? What unit or units does it carry?
Too often kids have trouble with word problems. Too often they don't know what to do with two numbers let alone a bunch of numbers. They guess at division when one number is big and one is small. They add when they see two fractions. They multiply because that was how they solved the last word problem.
I will also do this with my 8th graders because I suspect they will have trouble too. And this is exactly the kind of trouble we need to get into. Now rather than later. This task gets them thinking about ratios — which is like the most important math thing in all of the math things.
Steward is exactly right about this task. And I'm thankful he shared.
It was used as a fine example of how reversing the question can often lead to a more challenging task.
Multiplication: Finding the Greatest Product
From a set of 1 through 9 playing cards, I draw five cards and get cards showing 8, 4, 2, 7, and 5. I ask my 6th graders to make a 3-digit number and a 2-digit number that would yield the greatest product. I add, "But do not complete the multiplication — meaning do not figure out the answer. I just want you to think about place value and multiplication."
I ask for volunteers who feel confident about their two numbers to share. This question brings out more than a few confident thinkers — each was so confident that he/she had the greatest product. (I'm noting here that I wasn't entirely sure what what the largest product would be. After this lesson, I asked some math teachers this question, and I appreciate the three teachers who shared. None of them gave the correct answer.)
I say, "Well, this is quite lovely, but y'all can't be right." I ask everyone to look at the seven "confident" submissions and see if they could reason that one yields a greater product than another, then perhaps we might narrow this list down a bit.
Someone sees "easily" that #7 is greater than #6. The class agrees.
Someone says #7 is greater than #1 because of "doubling." She says, "I know this from our math talk. Doubling and halving. Look at #1. If I take half of 875, I get about 430. If I double 42, I get 84. Both of these numbers [430 and 84] are smaller than what are in #7. So I'm confident #7 is greater than #1."
Someone else says #5 is greater than #4 because of rounding, "Eight hundred something times 70 is greater than eight hundred something times 50. The effect of multiplying by 800 is much more."
Someone says, "Number 2 is also greater than #1 because of place value. I mean the top numbers are almost the same, but #2 has twelve more groups of 872."
But the only one that the class unanimously agrees on to eliminate is #6. Then I ask them to take 30 seconds to quietly examine the remaining six and put a star next to the one that they believe yield the greatest product. These are their votes.
I tell them that clearly this is a tough thing to think about because we've had a lot of discussion yet many possibilities still remain. And that's okay -- that's why we're doing this. We've been doing enough multiplication of 2-digit by 2-digit during math talks that it's time we tackle something more challenging. So #3 gets the most votes.
I then punch the numbers into the calculator, and the kids are very excited to see what comes up after each time that I hit the ENTER key. Cheers and groans can be heard from around the room. Turns out #3 does has the greatest product (63,150) out of the ones shown.
Ah, but then someone suggests 752 times 84. I punch it into the calculator and everyone gasps. It has a product of 63,168.
Their little heads are exploding.
I give them a new set of five for homework: 2, 3, 5, 6, and 9. They are to go home and figure out the largest product from 3-digit by 2-digit multiplication. They come back with 652 times 93.
The next day, we try another set: 3, 4, 5, 8, and 9. We get the greatest product by doing 853 times 94. There is a lot — as much if not more than the day before — of sharing and arguing and reasoning about multiplication and place value.
Many of them see a pattern in the arrangement of the digits and are eager to share. They've agreed on this placement.
Then we talk about making sure we know we've looked at all the possible configurations. They agree that the greatest digit has to either be in the hundreds place of the 3-digit number or in the tens place of the 2-digit number. We try a simple set of numbers 1 through 5, and we agree that there are just 9 possible candidates that we need to test. The same placement holds.
Then we draw generic rectangles to remind us that we've just been looking for two dimensions that would give us the largest area.
I remember saying to the class, more than once, that this is tough to think about. To which Harley, sitting in the front row, says, "But it's like we're playing a game. It's fun."
Two Pizzas and Five People
I'm thinking a lot about how my 6th graders responded to a pre-lesson task in "Interpreting Multiplication and Division" — a lesson from Mathematics Assessment Project (MAP) .
MAP lessons begin with a set structure:
Before the lesson, students work individually on a task designed to reveal their current levels of understanding. You review their scripts and write questions to help them improve their work.
I gave the students this pre-lesson task for homework, and 57 students completed the task.
I'm sharing students' responses to question 2 (of 4) only because there's already a lot here to process. I'm grouping the kids' calculations and answers based on their diagrams.
Each pizza is cut into fifths.
About 44% (25/57) of the kids split the pizzas into fifths. I think I would have done the same, and my hand-drawn fifths would only be slightly less sloppy than theirs. The answer of 2 must mean 2 slices, and that makes sense when we see 10 slices total. The answer 10 might be a reflection of the completed example in the first row. "P divided by 5 x 2 or 5 divided by P x 2" suggests that division is commutative, and P here must mean pizza.
Each pizza is cut into eighths.
Next to cutting a circle into fourths, cutting into eighths is pretty easy and straightforward.
Each pizza is cut into tenths.
I'm a little bit surprised to see tenths because it's tedious to sketch them in, but then ten is a nice round number. The answer 20, like before, might be a mimic of the completed example in the first row.
Each pizza is cut into fourths.
I'm thinking the student sketched the diagram to illustrate that the pizzas get cut into some number of pieces — the fourths are out of convenience. The larger number 5 divided by the smaller number 2 is not surprising.
Each pizza is cut into sixths.
It's easier to divide a circle by hand into even sections, even though the calculations do not show 6 or 12.
Each pizza is cut into fifths, vertically.
Oy. I need to introduce these 3 students to rectangular pizzas. :)
Five people? Here, five slices.
Mom and Dad are bigger people, so they should get the larger slices. This seems fair. We just need to examine the commutative property more closely.
Circles drawn, but uncut.
I'm wondering about the calculation of 5 divided by 2.
Only one pizza drawn, cut into fifths.
Twenty percent fits with the diagram, if each person is getting one of the five slices. The 100 in the calculation might be due to the student thinking about percentage.
Only one pizza drawn, cut into tenths, but like this.
I wonder if the student has forgotten what the question is asking for because his/her focus has now shifted to the diagram.
Each rectangular pizza is cut into fifths.
Three kids after my own heart.
Five portions set out, each with pizza sticks.
I wonder where the 10 comes from in his calculation.
Five plates set out, each plate with pizza slices.
Kids don't always know what we mean by "draw a picture" or "sketch a diagram." This student has already portioned out the slices.
What diagrams and calculations would you expect to see for question 3?
There's important work ahead for us. The kids have been working on matching calculation, diagram, and problem cards. They're thinking and talking to one another. I have a lot of questions to ask them, and hopefully they'll come up with questions of their own as they try to make sense of it all. If I were just looking for the answer of 2/5 or 0.4, then only 12 of the 57 papers had this answer. But I saw more "correct" answers that may not necessarily match the key. We starve ourselves of kids' thinking and reasoning if we only give multiple-choice tests or seek only for the answer.
That's why Max Ray wants to remind us of why 2 > 4.
Smallest and Largest
Most of my 6th graders struggled with this handout today. Only 4 of 36 students scored 8 out of 8 on it. I offered no help on this except my reading the instructions to them and reiterating that for each operation, the two numbers must be different.
I retyped this task from the Noyce Foundation.
If you teach 6th grade math or if you could share this with a colleague who does, I'd be very curious to learn how your kids might do on this. (Guess I'm now wondering how 7th and 8th graders fare on this too.)
I'm feeling disheartened and ineffective with this group of 37 kids. If I squinted really hard, then maybe I could spot just a few tiny specks of mathematical growth in them.
This teaching thing is tough.
Visualizing Volume is Tricky!
This was one of those lessons that I think I gained a lot more than my 6th graders did. It was meant as a one-period activity, but I kept going off on different tangents and brought the students along for the ride.
Over a month ago Andrew Stadel tweeted me a picture that he took of a William Sonoma display of their cupcake mixes. I was at our local mall last Sunday and saw a similar display. We both thought about buying the mixes to make cupcakes for our kids, but it was $15 a can, and we'd need three, so the poor teachers said no can do.
I projected the images above and asked the kids to give me a guess of how many dozens or how many individual cupcakes can the large container make when the small [real] container can make 1 dozen or 12 cupcakes.
Their guesses were all over the place, ranging from 47 to 994 cupcakes. (We were very careful whether the submitted guesses were in "dozens"or in "individual cupcakes.")
So I did the only thing I knew. I replicated the two cans so the kids could see them physically in the room instead of just on a still photo. Granted the large "can" made from butcher paper was pretty awful.
But, before I asked for another guess at the number of cupcakes, it occurred to me that I wanted to know if kids were better at guessing one and two-dimensional items.
Question 1: How many times taller is one segment than the other?
The two segments below are proportional to the heights of the two cans.
Their estimates:
Question 2: How many times longer is one circumference than the other?
The two circles are proportional to the cans' tops/bottoms.
Their estimates:
Question 3: How many times larger is the area of one circle than the other?
The two circles are proportional to the cans' tops/bottoms.
Their estimates:
Then, I let the kids — row by row — come up to get a visual check at the paper replicas of the cans. But they may not manipulate the models because I was more interested in seeing the difference between their guesses of the still photo and the physical models.
Their estimates:
If I wrote this post as Dan's 3-Act Lesson, then it was time for Act 2: figure out the volumes of the two cans using their measurements. (Yes, I carry a measuring tape wherever I go now.)
I tried to show the kids equivalent measures whenever possible. We worked a lot with centimeter cubes this year, so this was a rare time that we measured in cubic inches.
And here are some estimates from grown-ups who only saw the left image at the top of post:
(Got more guesses after I printed this: 1,000, 182, 600, 576.)
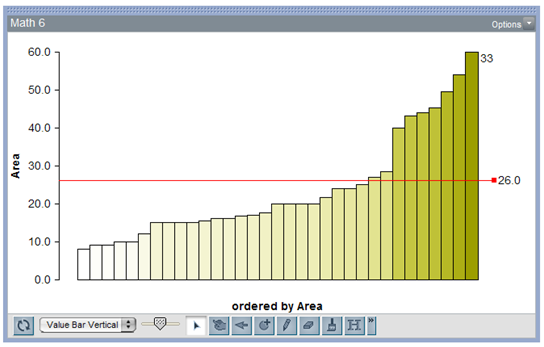
The straight lines [heights] seemed easiest to estimate. It got a little bit tougher when these lines bend into circles [circumferences] — and there was a large number of over-estimates here. I thought area estimates were pretty good, average of all 33 student guesses was 28.3 (calculated was 26).
The volume estimates, from kids and adults, remained well under the calculated numbers. I don't know what to make of all this. But I kept wondering: Are boys or girls better at making volume estimates? (From my small sample of 33 students, the girls were closer.) How about science teachers? The 3D models helped overall; and I bet if I let the kids do everything but measure the cans, their numbers would be closer. Interestingly, at one point I'd placed the smaller can inside the larger can, and kids who stood nearby kinda gasped. One said, "Oh, you can fit a lot inside."
Thank you, once again, to Andrew for sending me that tweet that started all this! He did a wonderful presentation of 3-Act Lessons to his staff.
Why Wait for Calculus?
(I just had my very best lesson yesterday, on a Friday, thank you. I feel almost brilliant right now. And I only feel like this once every 47 years, so please stay and read this post!)
My own kids tell me they will stock up their dorm rooms and apartments with junk food and soda when they move out to make up for these years of deprivation. (And this is supposed to make me feel bad.) So when I intentionally bring home a snack, like this bag of kettle corn, I usually find it empty within 24 hours. But seeing the empty bag made me think of a volume activity that I could do with my 6th graders with all these other bags of Orville Redenbacher's popcorn.
But the activity I had in mind — maximizing the volume of a box — is commonly done in a pre-calc or calculus class. These are my 6th grade babies. But didn't we do okay with approximating the volume of a torus via my doughnut lesson? So, why can't we do this too? I have to get rid of the popcorn.
I randomly assigned the kids in pairs, gave each pair two sheets of white copy paper. I told them to use one paper at a time to make a box — the goal is to make the box as big as possible so it'll hold the most popcorn. But the box must be made simply like this: cut off 4 corners from the the paper, then fold up the sides and tape them together. I used a half-sheet (so they couldn't duplicate mine) to demonstrate what I meant.
They quickly went to work. A few students were NOT cutting off square corners, so the top edges of the sides didn't line up. Two groups folded in their papers, in addition to cutting off corners, so they had to re-do.
Ryan and Annamaria wanted to make a shallow box. Ryan said, "... it doesn't matter how high it is."
Rapha and Cristian made the biggest corner cuts that I saw in the first round.
Mike's and Roy's first box was the shallowest in the class, but they changed their mind for their second box.
With 10 minutes left in our first hour together, I asked the kids to measure the box and find the volume. They had no trouble with this since we did the doughnut. They recorded the volume inside each box, and I tacked them on the board. (The butter seeped through in few of the boxes.)
Well, that was fun. I pointed out that two of the bigger boxes were over 1,000 cubic centimeters. The bell rang. I said, "We'll wrap up this afternoon."
I didn't know what I was going to do to "wrap up" the lesson. The microwave actually overheated — my room stank of greasy popcorn.
There was a confidence in me, however, that the kids would help me figure out how/where this lesson could go next. I began the afternoon hour by going over what they'd learned in the morning. They said:
The four corners must be of the same size. (I never told them this in my instruction.)
Each corner must be a square. (I didn't tell them this either. Not everyone was convinced of this, so I cut non-square corners to show them.)
There was a limit to how big the square could be. (I loved this! And this made me ask, "Is there a minimum to the size of the square?" Their eyes squinted, almost as if they were trying to "see" how small these corner squares could get. One kid said, "No. Technically, no.")
The volume numbers that people wrote down could be wrong.
By then they understood the different boxes and their volumes depended on the size of the corner squares that would get cut off. We focused on this. I asked them to draw a 10 x 12 rectangle in their math journal. We removed 1 x 1 corners from this rectangle and found the volume. I guided them through the next 2 x 2 corners. They continued on their own.
Then I gave each kid another white piece of copy paper. We measured the length and width of the paper and agreed that the paper was 28 cm x 21.5 cm. I asked them to build a systematic table like the one they just did in their journal. I said something like this, "Because you now know how to figure out the volume without actually cutting and making the boxes, see if you could figure out what size square the corners should be to maximize volume."
I saw kids high-fiving each other, "The corner has to be 4 by 4!" Rapha and Cristian beamed after congratulating each other, "That was one of the boxes we made!" We ended class with that. I swore I felt myself tearing up.
On Monday we'll play around with this applet.
And we'll ask Wolfram Alpha to take the first derivative of the volume for us. (I'm pretty sure the class could write this equation V = (28-2x)(21.5-2x)(x) for me to enter into WA.) Well, I actually just did it, and WA gives the side of our corner square as approximately 4.01965. My kids got 4 — pretty damn good for 6th grade brute-force math. Now that I'm writing this, however, I am really most proud of how well the kids had worked together. I randomly paired them up — a handful of the pairs were like the odd couples: high/low, shy/outgoing, squirrelly/quiet, jock/nerd, princess/cowboy. There was not a whisper of whine when their names were called to pair up. How did I get so lucky?
I am a doughnut.
I cannot eat a doughnut without thinking of Eddie Izzard. Language caution in this video clip.
Ich bin ein Berliner aside, I needed a calorie-laden lesson for my 6th graders to welcome them back into the classroom after two beautiful spring break weeks.
(We are also two short weeks from state testing and should be reviewing for the test. But who wants to do that when one can eat a doughnut instead?!)
I got the idea for this lesson from NCTM.
Estimating Volume
I held up one doughnut and a centimeter cube and asked each student to write down an estimate of the doughnut's volume in cubic centimeters. But first, I needed to tap the kids' prior volume knowledge.
Me: So, what is volume? What is the volume of this doughnut?
Julia: Length times width times height.
Me: Hmm... Where is the length of this doughnut? Or its width?
Julia: Oh...
Matt: It's the inside of something.
Sam: But that's area.
Rapha: It's the whole thing. The doughnut itself.
Matt: No, I mean the space inside.
Julia: Oh... it's how many of those cubes fit inside the doughnut!
I always dread hearing kids give me a formula for anything unless I specifically asked for a "formula," but this time I didn't break into hives.
I asked if it would be okay that I just counted the centimeter cubes in each of the solids below to find volume. The kids immediately pointed out the empty space inside and one said, You have to add like 5 to your answer to make up for the space. Another student said, More like add 10.
The class agreed that the cylinder held more cubes than the sphere and that the doughnut would be bigger than the cylinder. I told them there were 69 green cubes in the cylinder and allowed them to change their doughnut volume estimate if they wanted to.
When a centimeter cube was placed on the doughnut box, almost everyone said, Wow! (This made me happy because it showed they thought of volume as volume, not length-times-width-times-height.) They recorded their estimates for the box's volume.
Estimating Surface Area
When I asked the kids about SA, they said the outside, all-around, total area, all the surfaces, and doughnut skin represented SA. I added that the amount of glaze could also represent SA.
I told them this grid paper had 22 by 18 rows or 396 square centimeters and asked for their estimate of the doughnut's surface area.
They also recorded their estimate of the box's surface area.
Measuring the Doughnut
To manage this potentially messy lesson, the doughnut had to stay on construction paper, and all measurements had to be taken with a paper ruler.
Students took as many different measurements of the doughnut as they thought necessary to figure out volume and surface area.
They ate the doughnuts, and Cristian wanted me to take a picture of him.
We'll wrap up the lesson tomorrow and discuss approximating for volume.
No, none of my 6th graders brought up any of these -us words: torus, annulus, calculus. However, we did a lot of estimating and measuring with visual and concrete models. We each gained 200 calories from this.
Updated 04/17/12
In my comment, I told @Peter_Price about making a cylinder similar to the doughnut; then, I found this roll of masking tape that was close in size!
My 6th graders are familiar with area, so surface area was easy to grasp. (I felt smart when I could just peel off the tape to show the side SA.) I showed them my set of vinyl nets to the geo solids also.
I needed the students to figure out how to calculate volume on their own. I used these two models because of both the CDs and the patty paper sheets are very thin.
Student A: Find the area of one sheet and multiply by how many sheets there are.
Me: There are 1,000 sheets here, so area times 1,000 gives me volume?
Student B: No, that just gives you the area of 1,000 sheets, kind of like their surface area, but you're still doing area, aren't you?
Me: It would seem so.
I told the class that finding the area of one sheet was correct. And they also knew that it was the same area as the base of the box. Then I poured out the stack of CDs and started filling its container back up one by one. (Easier than stuffing the patty sheets back in.) I said quietly. Volume is three-dimensional.
The class watched, and soon, the hands went up. Before I could call on anyone, a few students couldn't contain themselves and violated our classroom rule of waiting to be called on before talking. Two kids yelled out, The height! Then more chimed in to say, Multiply by the height!
Always Sometimes Never
I did Always-Sometimes-Never (ASN) questions with my 6th graders. The kids were randomly paired up to work on placing 18 mathematical statements into the appropriate columns: always true, sometimes true, and never true.
The students were involved in the discussion and coming up with examples. They had to translate some statements into equations or inequalities and defend their answers. They learned to give counterexamples.
ASN works for any math level (and could be used in other subjects). The kids are comfortable working and having that math conversation with just one other person initially; then, they build up the confidence to share their reasoning with the whole group later.
I got this particular set of 18 from Swan and Ridgway. Sixth Sense has a set also.
Here are the statements we used:
Max gets a pay raise of 30%. Jim gets a pay raise of 25%. So Max gets the bigger pay raise.
When you cut a piece off a shape, you reduce its area and perimeter.
If you add the same number to the top and bottom of a fraction, the fraction gets bigger in value.
In a sale, every price was reduced by 25%. After the sale, every price was increased by 25%. So the prices went back to where they started.
(a+b)/2 ≥ sq(ab)
If you divide the top and bottom of a fraction by the same number, the fraction gets smaller in value.
It doesn't matter which way you multiply; you get the same answer, like 𝑎 × 𝑏 = 𝑏 × 𝑎.
If you add a number to 12, you get a number greater than 12.
The square root of a number is less than the number.
It doesn't matter which way you divide; you get the same answer, like a ÷ b = b ÷ a.
If you divide 12 by a number, the answer will be less than 12.
The square of a number is greater than the number.
p + 12 = s + 12
n + 5 < 20
2(x+3) = 2x + 3
3 + 2y = 5y
4p > 9 + p
2(3+s) = 6 + 2s