My Other Math Sites
Lessons From the Classroom
Barbie Bungee Revisited and Better Than Yours Class Lists
This year I've taken away a lot of my step-by-step instructions for the Barbie Bungee activity that I'd posted 1.5 years ago. They get no handouts, only some verbal instructions:
[Pointing to the ceiling] See that gob of tape up there? That's leftover tape from previous years where Barbie had taken her jump. It should be at 3 meters up. Well, a small ruler will come out perpendicular (somehow) to that pole where the tape is, and that's Barbie's jumping platform. The ruler is like her diving board.
The goal is to give her the most thrilling jump — her head dips as close to the ground as possible without actually touching it. Yes, her hair hitting the ground is fine. Her jump line is made of rubber bands tied together with slip knots. (Why must we use brand new rubber bands?) You'll work in groups of three, says Instant Classroom.
So, aside from the Barbie doll, what do you think your supplies will be?
Rubber bands! How many? Lots! A hundred!
Try six. Actually seven, but one must be completely wrapped around her ankle, like this.
With only 6 rubber bands, your job is to figure out how many more rubber bands she'll need for the most thrilling jump from 3 meters.
Can we weigh her?
This is like the Vroom car!
So we have to graph, then do the extension thingy. Extrapolate. Oh, the equation is in slope-intercept form!
(We've been looking at word problems and writing linear equations that would be more appropriate in standard form or in slope-intercept form.)
Your team will have until the end of tomorrow's class time to submit your number of additional rubber bands you'd want.
For easier management of the rubber bands, I get them ready in bundles of 7, one to each group for testing and data gathering, and in bundles of 10 and extras to give out as requested on jump day.
I liked the messiness of their initial work. (I didn't give a handout or many instructions for Vroom! either, and they did fine.) Kids doing whatever they think they should do, measuring incorrectly, plotting ill-looking graphs, talking and criticizing one another. I was debating when I should intervene, but it was good for me to just observe and listen in.I waited until the next day to point out stuff. Actually I never told them what they should do, I tried instead to ask them how something should be done. I don't think one single idea came from me — someone always had the answer I was hoping for, so all the "correct" ways to do things came from them. My phone apparently didn't have enough memory after this one clip. It was fun. (One kid also brought up that this was like the Stacking Cups lesson that we did.)
This might seem to you a DUH! share, but I only thought of it earlier this year, and I feel like I invented the paper clip. We all have class lists, of course. But is each of your class lists on a strip of paper like this? And in different colors? I didn't think so.
I have semi-thick stacks of these to use for just about everything. What a pain to write down kids' names for this and that. Instead I just pull out a strip and highlight so-and-so's name and note the reason.
I staple one set of strips together, put a date on it, and kids pass it around to each other to sign in for after-school help — they just need to put their initials next to their names.
Those who need to come in at lunch recess get their names highlighted on the strip.
I use it as a hall pass when I need to send 2 to 3 students at a time to the library.
I highlight a kid's name whose parent I need to contact, then use the back of the strip to make notes from our conversation.
It's a great tally sheet for whatever during class.
Endless uses.
Des-man
Not only was this so great to reinforce slope, y-intercept, and all the coefficients, it also allowed us to talk about domain and range.
What I heard around the room (that I can remember):
Oh, I get this now! I see what changing this number does!
Oops, I made his face too wide!
His smile is crooked. But I think I'll leave it because he looks cool that way.
Ha!! I see my mistake, I said x had to be greater than 4 but less than 2. Silly me.
I want the eyes to be oval shaped though. My plan is to make 2 parabolas opening into each other.
Can we work on this in 6th period too?
When I saw two students whose graphs were circles for faces, I knew they'd copied these from Desmos gallery as we haven't — and won't — learn circle equations in Algebra 1.
I reminded them of the minimum requirements, but I told the class that they may copy equations and tinker with them to add other features, such as hair and whiskers. (I actually said "whiskers," and Lexi had to tell me, "Whiskers? On a man? You mean beard or mustache?") People don't have whiskers? Good to know.
I made my guys' eyes elliptical and tweeted it, the good folks at Desmos responded.
So cool!
I think we got a lot of mileage from this activity. It's a good sign when teacher instruction is minimal and student engagement and discussion are high.
Just in case you missed the Grand Opening of Daily Desmos about 3 weeks ago, brought to us by Michael Fenton, inspired by Dan Anderson.
Stack 'em High
My algebra kiddos are doing Dan Meyer's Stacking Cups because Andrew Stadel did the lesson and wrote glowingly about it. But Andrew used only one-size cups, I used three different sizes.
Just eyeballing
I ask students to look at me, look at this 12-oz Styrofoam cup that I'm holding, and estimate how many cups they would need to stack to reach my height. I tell them I will not answer any clarifying questions regarding this, "just make your estimate in whatever way you think I mean by this." (Their hands shoot up anyway, but I remind them I won't answer any questions right now. It's clear that they want me to define "stack.")
They write their answers on a quarter sheet of paper. Here are their 29 estimates, the median at 24 cups.
Given the heights
Then I tell them my height is 163 cm with the flat shoes that I have on. I carefully measure the cup's height in front of them, we get 11.25 cm.
Equipped with this knowledge, I ask the same question as above. Their 28 answers yield a median of 14 cups. Of course Dan had already anticipated this — most students just divided my height by the height of the cup.
Stack 'em like this
I now ask them what it was that they'd wanted to ask me earlier. Sure enough Eddie says, "By stacking do you mean bottom-to-bottom, then top-to-top, or... one inside another?" I give him some cups to show me. At this time at least 2/3 of the kids admit that they answered the previous questions believing that I meant to stack the cups the way Eddie just described formerly. (This is consistent with the low guesses we see in the top image.)
I ask the next question, "Okay, I need you to answer the same question again of how many cups it'll take to reach the top of my head, but you now know exactly what I mean by stack, and you also know my height and the cup's height. Here, I'll even stand on this table with 6 cups stacked at my feet so you can see. Go, give me a number.
Here are their 27 estimates, and 113 is the median.
We're just getting started
I randomly pair kids up. (Normally they are in groups of 3, but I think it's better to be in pairs for this activity.) I give each pair 6 cups. They have the last 25 minutes of class to figure out:
The equation for this problem
The number of stacked cups for my height
Some groups need help with finding the y-intercept. A few groups don't know where to begin. I ask them some questions and walk away. They plan to nominate me in June as their most non-helpful teacher. Whatever.
I like this group's drawing, even though the lip and body of cup do not add up correctly.
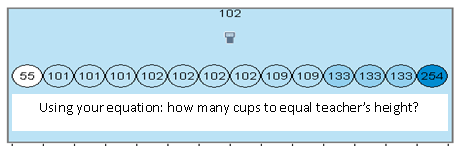
Using their equations
The majority of the groups figure that the lip of the cup is the slope, but many groups also think that the full height of the cup is the y-intercept. Using their equations to figure out the number of cups, they give me these numbers.
Not too shabby. My equation yields 102 stacked cups to reach top of my head, and that happens to be the mode and median.
And the actual number of cups is...
This is the moment they've been waiting for! I have 81 cups stacked already when the kids come in the next day, then they count out loud as each additional cup is added to reach my height. Our principal is paying us a visit today, and he keeps telling me how impressed he is with how engaged the kids are and how hands-on the lesson is. He helps with the countdown too and officially announces that it takes 100 cups to stack up to my height! (Three groups whose estimates of 99, 101, and 102 are having pizza with me next week!)
Getting our principal in on the fun
Working backwards. I tell the kids that it takes 116 cups to reach the top of our principal's head. How tall is he? Their answers give a median and a strong mode of 184 cm. His actual height is 183 cm!
Twice the volume and half the volume
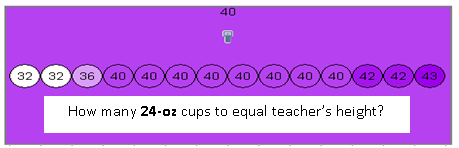
Just when they think they're done, I pull out the 24-oz and the 6-oz cups. It's not often that I hear them shriek in delight to do more math! The pair of students now gets only 3 cups of each new size. They go to work.
My height is 40 24-oz cups and 126 6-oz cups. Their calculations are great for the big cups, not so much for the little ones.
This ranks up there as one of my favorite lessons. Thanks much to Dan for another fab activity. But due to us having already passed linear equations, I honestly would not have done this lesson now without Andrew's push.
Updated 02/06/13
Eight more kids will join me for a pizza lunch for getting the equations to the 24-oz cups correctly. And here's a pic of me and the 3 stacks. The boys are 6th graders helping me hold up the stacks.
Barbie Bungee
I bought a 1-lb bag of rubber bands for my Barbie Bungee activity today.
We should have done Barbie Bungee earlier in the year while learning linear equations and lines of best fit, but better late than never. My collection of Barbies could use some refurbishing work — they get used so much each year for this activity and for our lesson on proportions.
OBJECTIVE: Create a bungee line for Barbie to allow her the most thrilling, yet SAFE, fall from a height of 3 meters.
I randomly assigned students to groups of three. Each group got their own Barbie and 7 new same-size rubber bands. My instructions:
Measure Barbie's height. Record this as rubber band length of 0.
Connect 2 rubber bands with a slip knot.
Wrap one of the two rubber bands tightly around Barbie's ankles.
Drop Barbie, holding the rubber band level with the meter stick.
Record Barbie's fall using the lowest point her head reaches in centimeters. This number is your rubber band length of 1. (The rubber band around her ankle is not counted in the length of the line.)
Add another rubber band, drop Barbie, and record. Do this for a total of six rubber band lengths.
Measuring: They quickly went to work. (We're lucky to have good weather here pretty much year-round because I need some students to be outside whenever we do projects like this — they need to spread out to do the work.)
Graphing: The groups graphed rubber band lengths vs. distance of fall. Then they drew in the line of best fit. From this line, students predicted the number of rubber bands for Barbie's bungee line that would be thrilling enough for her 3-meter jump without cracking her head open!
Once groups made their prediction — written on their papers and on the board — they may not change it. I had taped a small ruler to that rod to mark the 3-meter height. I can't have students on the ladder, so that's me getting ready to drop a Barbie. (The numbers on the left were their initial guesses before doing anything else.)
This was a blast!! I had two kids lying on the ground with meter sticks to watch and measure Barbie's initial plunge; they were our judges. We clearly had a winning jump when one group's Barbie came within 2 cm of the floor. They asked if they could get a second chance, so all 10 dolls had another jump after adjusting the number of rubber bands on the bungee line.
What I heard around the room
I noticed the centimeters went up by 10 on average.
Her height is the y-intercept.
Nine rubber bands is approximately 100 cm, so we need...
Stop stretching the rubber bands, you're gonna ruin our estimate!
Each meter stick is 98 cm. (His two teammates did not say anything when they heard this!)
I have to re-do our graph. I stuck it too close to the top, and the line of best fit has nowhere to go.
You're not supposed to connect the dots!
This was so much fun!
Oh, I didn't realize how stretchy the rubber bands got. (To which another student said, "Hello, it's rubber."
Ken is heavier [than Barbie]. We forgot this.
Hair centimeters! She was that close!
Notes
Barbies are Barbies. My kids are used to handling the dolls, a few of them have no clothes on (I got many of them on eBay). But I start every lesson with my usual warning that if I see anything remotely suggestive or derogatory done to the dolls, the student would be sent to the office and not be able to return to my class until I spoke with his/her parent. There has never been a problem in the last 8 years. The same applies to the rubber bands.