Good-Enough-for-Now Curriculum

I did my first webinar last week as a precursor to my talk at NCTM's Innov8 Conference next month. I thought it went okay — or horribly — just tough to be the only person with the mic and not being able to actually see the attendees. It was weird.

There are a few slides from the webinar that I'd like to share here mainly because I'm still thinking about them and writing anything down helps me set the wobbly gelatin.

Two weeks ago I presented at an independent school that's Preschool through Grade 8. Afterward, I was given a quick tour of the school — the 33-acre campus gleamed with pride in its thoughtful architecture, manicured grounds, state-of-the-art this and that, and a smorgasbord of elective offerings, including Mandarin and photography.

My school is Kindergarten through Grade 8, and the similarity between my school and this independent school pretty much ends there. I teach four classes, my smallest class has 23 8th graders, the other three, all 6th graders, have 32, 35, and 36 students. We're a Title 1 public school.

I bring up the private school and my public school because, like apples and pomegranates, they are quite different. So, when we do PD and share whatever it is that we share about education and serving children, we need to be mindful about the space that each teacher occupies in her building and be mindful about the children who come into that space.

When someone shares something with me, one or more of these thoughts cross my mind: 1) I can see how that would work with my students, 2) I can see how I might adapt this to fit my kids, 3) This person is afraid of children or unaware that children are people, 4) Nobody cares.

Likewise, when I have the stage to share, I'm assuming you have similar thoughts of my work. But I beg you to think about the space that I share with my students.

Below is a quasi rating scale of "critical thinking demand" that I'd created to place the types of tasks that I regularly give to my students. And this scale is only possible because I'm mindful of the tasks' contents and my own pedagogical content knowledge to facilitate these tasks.

What are these six things? The resources for these are on this spreadsheet.

1 & 2.  Assessment and Textbook: We're using CPM. [04/07/2022: We now use Open Up Resources and Desmos.]

3.  Warm-up: Due to our new block schedule, we've only been doing number talks and visual patterns. 

4.  Problem-of-the-Week

5.  Task

6. PS (Problem Solving)

Do these 6 things align to the curriculum?

The slide below shows the 4 types of tasks that are aligned to the curriculum, or that when I pick a PoW or Task, I make sure it correlates to the concepts and skills that we're working on in the textbook. Therefore, it's entirely intentional that the warm-up and PS are not aligned because critical thinking and creative thinking are not objects that we can place in a box or things that I can string along some prescribed continuum.

All 6 types of tasks are of course important to me. I try to implement them consistently with equal commitment and rigor to support and foster the 8 math practices.

Which ones get graded?

I don't grade textbook exercises, i.e., homework, because I can't think of a bigger waste of my time. I post the answers [in Google Classroom] the day after I assign them. I don't grade PS because that's when I ask students to take a risk, persevere, appreciate the struggle. I don't grade warm-up because I don't like cats.

I'm finally comfortable with this, something I've been fine-tuning each year (more like each grading period) for the last 5 years. I could be a passive aggressive perfectionist — or just an asshole when it comes to getting something right — so it's no small admission to say that I'm comfortable with anything.

It's about finding a balance, an ongoing juggling act between building concepts and practicing skills, between problem-posing and answer-getting, between teacher talk and student talk, between group work and individual work, between shredding the evidence and preserving it. Then ice cream wins everything.

Here's the thing. We want to build a math curriculum that makes kids look forward to coming to class everyday. I trust that that's true for more than half of my students — this could mean anywhere between 51% and 80%. I think we're doing something wrong when kids look forward to just Measurement Monday, Tetrahedron Tuesday, or Function Friday. Math should not be fun only when students get to play math "games"!

dudamath.com

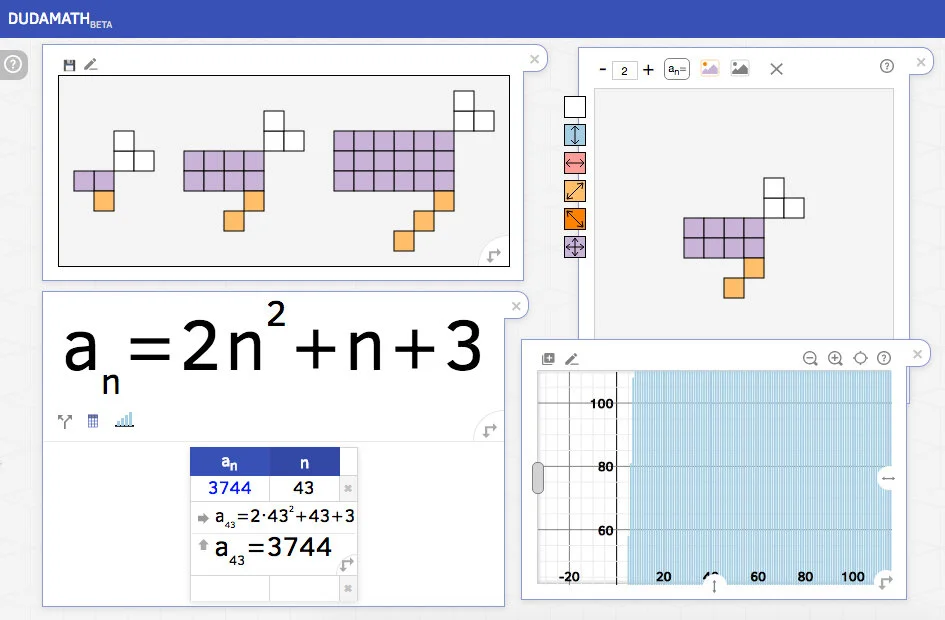
Ethan Hall, teacher and web entrepreneur from Israel, emailed me this morning asking me to check out his visual patterns generator on dudamath.com.There's a lot of cool graphing tools other than the VP generator.I'm kinda blown away. Go play! Go do math!

Dividing Fractions

My 6th graders have been working with dividing fractions for the last two weeks. We explore these four ways, in this order:

1. Number line

2. Rectangles — I wrote about this here.

3. Dividing by one

4. Common denominator

It's completely intentional that we work with the number line and rectangles first. I want my kids to see the answer and that it should match their intuition and understanding.

Google Classroom

Falling behind on #MTBoS30 already!

Here's my excuse. 

I'm loving Google Classroom. We have effectively gone nearly paperless by doing warm-ups, weekly PoWs, problem solving, almost anything and everything in Classroom. I appreciate the efficiency of organizing folders and the seamless integration with Google Drive. I still have a lot to learn, but I'm excited with how we're using Classroom already.

I put a visual pattern in Google Draw for students to mark up the pattern and figure out the equation.

Students complete a Google doc for other warm-ups.

Here's one we just started today.Students do PoWs (from NCTM The Math Forum) in Classroom, and I can give them feedback directly on there.

We save valuable class time by posting answers to textbook problems in Classroom.

You get the idea. I would love to learn how you use Classroom! Please share in the comments or hit me up on Twitter @fawnpnguyen.

Teacher Appreciation

Today I remember my 7th grade home economics teacher Mrs. Quiggle. Marge Quiggle. She was already old when she was my teacher. I didn't speak a whole lot of English then, but I suppose one does not need to be well versed in the language to sew a sundress or make a baked Alaska. A couple of months ago I started sewing again, and I thought about Mrs. Quiggle a lot, how she made me press open every seam before continuing on.

Then there was Mr. Anderson. He was my 8th grade social studies teacher. I had a crush on him. I don't know why because he was not particularly handsome. I worked extra hard to submit an extra awesome book report on Nigeria. Before I moved away (leaving Minnesota for Oregon), he gave me a picture of him standing next to his wife. Nobody cared about his wife of course, but he was my favorite.

Today I'm also reading my 6th graders' responses to this warm-up. The answer is there are 30 days left of school.

Joint Investment

Would you have known immediately that the number 1729 is the sum of two cubes?

You think you're so smart, but you're no Ramanujan. He told Hardy that 1729 is the sum of two cubes in two ways: 1³+12³ and 9³+10³.

I read The Man Who Knew Infinity a few years ago. I might check out the movie when it hits a theatre near me. Like Netflix.

Also, I subjected my students to this 14-minute podcast about Hardy and Ramanujan.

One more "fair share" task for my 8th graders from Peter Liljedahl's site because I like it and don't want to work in the textbook as our students are taking the Smarter Balanced Tests this week.

Joint Investment

Six years ago you made an investment with a friend – you bought a house together. It wasn’t only an investment, it was also a favor. Your friend didn’t have a place to live and didn’t have enough money to buy a house. So, you pooled your money and bought a $300,000 house for your friend to live in. You provided $50,000 for the down payment and your friend provided $25,000. Because of the size of the down payment it meant that the mortgage was relatively low – only $1000 a month – which your friend paid. During the six years all property tax payment were split evenly between you as were all major renovations and upgrades. Well, it is now six years later and your friend is getting transferred to Ontario. So, you have sold the house for $500,000 (the market has been good to you). There is still $200,000 outstanding on the mortgage. How will you split the $300,000 equity between you? Justify your decision.

Two groups of students have submitted their solutions thus far.

…

…

…

…

…

…

…

…

…

…

The Shoe Sale

This problem is from Peter Liljedahl's site.

The Shoe Sale

You decide to take advantage of a buy 2 pair get 1 pair of equal or lesser value for free sale at the local shoe store. The problem is that you only want to get two pairs of shoes. So, you bring your best friend with you to the store. After much deliberation you settle on two pairs of shoes – a sporty red pair for $20 and a dressy black pair for $55. You friend finds a practical cross trainer for $35. When you proceed to the check out desk the cashier tells you that your bill is $90 plus tax (the $20 pair are for free). How much should each of you pay? Justify your decision.

Peter lists this problem under "Senior High School (10-12)." I give it to both my 6th and 8th graders. I like this problem because I like hearing how kids think about "fair sharing." A few 6th graders think each person should pay $45. I don't think these kids have too many friends. (That was mean.)

One of my 6th graders says one person should pay 2/3 of the $90 and the friend pays 1/3. But her answers are $59.40 and $29.60, respectively. My math says 2/3 of 90 is 60, so I call her up to explain. She has her calculator in hand, and I see her punch in .66 while mouthing "two thirds."

It was an opportunity for me to yell and scream at the children for turning a perfectly good number of 2/3 into mush.

Giving Feedback With a Highlighter

I attended John Scammell's excellent 3-morning sessions on Formative Assessment at #TMC15. We were asked to share strategies that we may already be doing to give students feedback . I shared about how I used highlighters for this. I promised my group that I would write a short post about it, but I waited until now since I needed the school year to begin to have student samples to share.

I used highlighting to give my 6th graders feedback on their first PoW (Problem of the Week from The Math Forum).

It's challenging, as I hope all PoWs are, and even more so when it's the first one they get. I give no specific instructions on how they should write up their solution — nothing more than the usual "show all your work in order to receive credit." I want to see what raw stuff I get on this first submission. We'll worry about quality control soon enough.

I'm familiar with what I can expect with the first harvest of solution write-ups. One-fourth of the papers are pleasantly stellar, one-third show candid efforts (especially the ones with parents' writings on them), another third make me get up and stick my head in the fridge to find a cold-and-alcoholic beverage, and the rest of the papers remind me that some of my 6th graders are still working on finessing the opening of their combination locks.

Years ago I taught a writing elective. I was at the beach — at the Oregon coast — because that's where you should read and grade all writing papers. I forgot my red pen. I only had a yellow highlighter. The highlighter transformed my grading. I no longer cared so much about the writing mechanics — fuck spelling and punctuation and syntax. You got voice in your writing, kid. Your heart was wide open in this third paragraph. How did you know the rain smelled differently depending on what part of Portland you were in?

I highlighted sentences and words that spoke to me. I highlighted a brave sentence. I highlighted the weak ones also. The highlighter allowed me to interact with the kids' writings differently. I didn't add to or cross out anything they'd written. The highlighter didn't judge the same way my red pen was judging.

And that's the history of using the highlighter for me. But back to math. I have over 100 students and to write feedback for their bi-weekly PoW write-ups is all too time consuming. The different colored highlighters come to my rescue.

I'm going to continue using my binary scoring system because it worked well last year. I look through all the papers, separating them into two piles: papers that got it (full 10 points) and papers that fell short (1 point). These kids will get another week to revise their work and re-submit.

I use my yellow highlighter — just swipe it somewhere on their paper — to show that I'm having trouble understanding their work or that their work is lacking.

I use the pink highlighter to show that the answer is not clear, not specified, is partially or entirely missing.

I use another color (like green or blue) if the papers warrant another something-something that I need to address. I didn't need to with this week's PoW submissions.

If necessary, I will write on their papers directly. But I don't have to do too many of these because kids' mistakes, more often than not, are similar to one another.

When I pass the papers back, I tell students what each colored highlight means and what they need to do to revise their work, including coming in to get help from me. It's a helluvalot faster than what I used to do.

Desmos Puppy House

We don't cover quadratic in Math 8 this year, so we really can't do Des-man. I come up with "Puppy House" instead so my students can still create something that allows them lots of practice with writing linear equations with domain and range restrictions.

They draft the house on paper. The house needs to have a minimum of 6 slanted lines, 5 vertical lines, 5 horizontal lines, and one image of a puppy at entrance of house.

Below are the ones from my Math 8 Honors kids who learned quadratic last year. They completed these within one 55-minute period. So proud of Ashlynn for remembering how to write inequalities.

Riley

Andrew

Ashlynn

I'd love to see what amazing dog houses your students will create. (Someone create a flap door for me to play peek-a-boo with the puppy please!)

Students Practice Scoring Short-Text SBAC Responses

A few weeks ago I attended an all-staff PD at the County Office. During the morning session we scored samples of 2-point short-text items from grades 4, 8, and high school. It was time well spent. I wanted to duplicate that experience for my students with two goals in mind:

1. See how well they can interpret and use a scoring rubric.

2. For them to attend to the same thoroughness and precision in their own solution writing when it's their turn in May.

What I had my students do:

1.  Get to know the short-text item.

They worked on the grade 4 item below. This was intentional to diminish any math anxiety and to keep our focus on the scoring of the task.

While it was good to learn of my kids' different solutions, it was also disheartening (but not too surprising as they are the same ones who struggle mightily) to learn that 20% of my 6th graders did not get the correct solution for this grade 4 item.

2.  Go over the solution.

I collected their papers and just had a couple of kids share their strategies to the whole class. Considering 1 out of 5 kids in the room didn't quite know how to solve the problem, this step was really for them.

3.  Get to know the item-specific rubric.

I gave the kids quiet time to read the rubric, reminding them that they would use this rubric to score 9 students' solution responses. I told them that they could expect to return to the rubric over and over again as they scored each response.

4.  Score the responses.

I gave them quiet time to fill out Score 1 column of this handout. I reminded them that this was one of the main goals of the task -- to score the sample responses fairly and accurately using the item-specific rubric.

Why are you giving this response a 1? What is it missing to not get a 2? What does it have to earn a 1 and not a 0? Keep referring to the rubric! Does spelling matter? What does your rubric say about spelling errors?

After everyone was done filling in Score 1 column, I asked them to talk to their neighbor/s and only fill in Score 2 column if they changed their mind. (They were not to erase any score in Score 1 column.) This also made it easy for me to see how many scores they'd changed their mind on.

My favorite thing in the whole wide world is to listen in on their conversations about math.

5.  Reveal the actual scores.

[The actual scores are on 2nd page of handout above.]

If the whole class agreed with the actual score for a particular student response, then we moved on. But if anyone disagreed, then I had that student tell the class why. Then I had another student who agreed with the answer to share his/her reason.

Out of 66 students, 24 students scored 9 of 9 correctly, 19 students scored 8 of 9 correctly, and 6 students scored 7 of 9 correctly.

That meant 65% of my 6th graders did this scoring-using-a-rubric better than I did. Whatever.

I also asked the kids to write a couple of sentences about what they got out of doing this. Most of their responses echoed these:

This was helpful to me because now I know I need to be much more thorough with my work and explain why I might of did something.

This was helpful to do because it let us see how these problems are graded.

Even though the problem was for 4th grade, I think the grading scale of conclusion and math will be similar or the same for all problems like this.

I believe this was helpful because when I take the test, I will be more aware of the questions and what is expected of me. I will make sure to always back up my answers with evidence.