My Other Math Sites
Lessons From the Classroom
Grade 6 Rocks Visual Patterns
I'm always happy to hear how teachers use visualpatterns.org with their students.
Michael Fenton shares how he uses the patterns with Desmos. And this.
Alex Overwijk's students use the big whiteboards.
Whiteboard photos of http://t.co/ajYFLzRQSU that my S's did yesterday....thanks @fawnpnguyen #mtbos #mathchat pic.twitter.com/UZd3HPfyoL
— Alex Overwijk (@AlexOverwijk) March 7, 2015
Bridget Dunbar removes some figures, and kids need to draw them in.
Visual Patterns and Missing Figures https://t.co/QDvPNlKRSZ Thank you @fawnpnguyen
— Bridget Dunbar (@BridgetDunbar) March 5, 2015
Kristin uses the patterns with 5th graders.
Snowflake Visual Pattern work in honor of our non-snow day! cc @JustinAion @fawnpnguyen #visualpatterns #mtbos pic.twitter.com/n6SZuigK5X
— Kristin Gray (@MathMinds) January 28, 2015
I do patterns with my students on Mondays as part of our warm-up routine. I've already shared 28 pattern talks (and 28 number talks) on mathtalks.net, but I'd like to share a couple more here because my 6th graders have made incredible gains in seeing a pattern in different ways and in articulating an equation to go with each visual.
This is pattern #153. I'm sharing this one because I meant to only use it with my 8th graders, but my printer was acting up and failed to print a different one for my 6th graders, so I just used the same one. Fun challenge!
Student 1:
I see these 5 spokes coming out. Each one has n number of hexagons. In between these 5 are Gauss. So, the equation is... five times n, plus five Gausses.
Hexagons = 5n + 5(1+n)(n/2)
Over time, my students have come to recognize Gauss addition very quickly. They have used Gauss as a verb and a noun, as in, I Gaussed it or I saw two Gausses in the pattern.
Student 2
Each step adds another ring of hexagons on the outside. Looking at the outer most ring, I see three groups of (n+2), plus a leftover. The leftovers are odd numbers. So, the outer ring alone is 3(n+2) + 2n-1.
And the rings add like Gauss!
Together we write the equation carefully, talking through each step.
Gauss means adding the first and last steps together, then multiply by the pairs of steps. The last step is the outer ring, the first step is the inner ring, which is always 10. So, 10 plus the outer ring, then multiply this by the number of pairs [of rings], which n/2.
Hexagons = [10+3(n+2) + 2n-1](n/2)
We were confident we had the correct answer when both equations simplified to the same equation.
Hexagons = [(5n^2)+15n]/2
This is pattern #147. I'm sharing this one because of the many different ways kids tried to see the pattern. Normally, when I randomly call on a kid to share and someone had already shared their same way of seeing, then they just have to come up with a different way.
Ducks = (n^2) + (2n+1) + n
Ducks = (n+1) + (3+2n+1)(n/2)
Ducks = n(n+2) + (n+1)
Ducks = 2(1+n)(n/2) + (n+1) + n
Ducks = (n+1)(n+2) - 1
Ducks = (n+1)^2 + n
I very intentionally do not have kids fill in a table of values for visual patterns. I'm afraid it becomes a starting point for them every time instead of just looking at the pattern itself. For our 8th graders using the CPM curriculum, which I like a lot, there are plenty of opportunities in the textbook to tie all the different representations (table, graph, rule, sketch). These are my 6th graders who are writing quadratic equations without all the fuss right now.
Please continue to share the site. What I love most is learning that the patterns also get used in elementary and high school classrooms.
Reversing the Question
Don Steward posted this on Sunday. Like Don, I really like this task and also think it has a certain Malcolm Swan je ne sais quoi about it.
I showed only the top part to my 6th graders, and I gave them 2 minutes to write down what they noticed.
In addition to noticing the given information, the students also mentioned:
It takes a lot of grams to make a sponge cake.
A kilogram must have a lot of grams in it.
The unit of measurement is changed in the cake and in the big bag.
This problem doesn't have a question.
The sponge cake has no price.
There is frosting on the cake.
You need to change the measurements first (kg - g)
The cake weighs more.
The cake is really small and the flour is really big.
Not much information and there's no question.
There is no question.
The weight of the bag is in kg but the flour it takes for the cake is in g.
You have to convert 24 kg to grams.
It uses only very little of the flour.
I gave them another 2 minutes to write down what they wondered.
How much the sponge cake costs.
How many sponge cakes can you make.
How big is the sponge cake.
How to convert from kg to g.
If the sponge cake is good.
24 kg is <, =, or > 150 g.
What we are going to have to solve.
Is the question going to be about if there's enough flour or is it going to make us change it from kg to g.
How much 24 kilograms is in pounds.
How many grams are in a kilogram?
How many krumkakes can you make with the bag of flour.
How long will it take for the cake to be ready.
What a sponge cake is and what the recipe is for the cake.
How much flour is left.
What flavor is the cake. (Sorry. I'm hungry!)
What you're wondering that I'm wondering about.
What the question is, and if there are more ingredients.
If we will have to find the price for the sponge cake, or maybe we have to find out how much half as much flour is worth.
Then we moved on to next part of providing questions that would go with the calculations. This was so very tough for my kids. While 21 of 31 kids could come up with the correct question for part (a), they were lost with what to write for the other three parts.
Because we didn't care what the numerical answers were, the kids didn't do any calculations, instead they were supposed to focus on the operation(s) in each problem and decide on the question that would prompt a specific operation.
The most common question for part (b) was, "How much does 1 kg of flour cost?" (I'd swapped out £ for $.)
Then my next step would be for them to go ahead and use a calculator to get the numerical answers. They will see that for part (b), 24 divided by 21.50 equals approximately 1.12. And if 1.12 were the cost for 1 kg of flour, then 24 kg of flour should cost more than $24. But, wait. We already know that the bag of flour costs $21.50. Hopefully they'll arrive at this contradiction on their own, and re-think their question.
We'll then attach the units to the numbers accordingly and let the conversations continue. When kids tell me that they will calculate two numbers using operation w, I always follow up with, What does your answer mean? What unit or units does it carry?
Too often kids have trouble with word problems. Too often they don't know what to do with two numbers let alone a bunch of numbers. They guess at division when one number is big and one is small. They add when they see two fractions. They multiply because that was how they solved the last word problem.
I will also do this with my 8th graders because I suspect they will have trouble too. And this is exactly the kind of trouble we need to get into. Now rather than later. This task gets them thinking about ratios — which is like the most important math thing in all of the math things.
Steward is exactly right about this task. And I'm thankful he shared.
It was used as a fine example of how reversing the question can often lead to a more challenging task.
Greenies
Our black lab Mandy is 3.5 years old, weighs a ton, and her breath used to smell like death. Until we started giving her one Greenies a day. My husband orders them from Amazon, he also gets them for our neighbor's small dog Bailey.
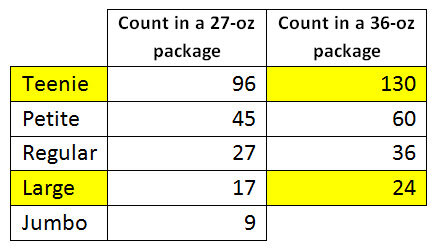
Although both boxes weigh the same 36 ounces, Bailey gets 130 treats in the Teenie size and Mandy gets only 24 in the Large size. This caught my attention which led to this task with my 8th graders who happen to be working with similar shapes. (Like I had planned this all along.)
Greenies are sold in various size packages. I'm interested in the 27-oz and 36-oz.
To launch the task, I hold up the 2 treats: 1 Large and 1 Teenie. I tell them that there are 24 Large ones in a 36-oz package, and I want them I guess how many Teenie ones are in a 36-oz package.
Then I give the students these:
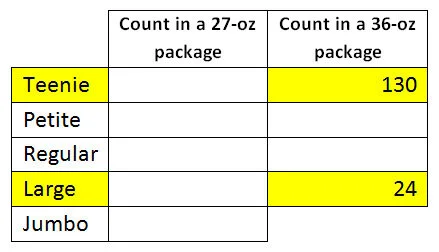
The photo of the 2 packages (so they know only the highlighted information in the table above).
Each group of 3 students get two real treats: 1 Large and 1 Teenie.
In return, the students need to give me these:
A 2-dimensional outline (with dimensions labeled) of what a Petite, a Regular, and a Jumbo may look like. For example, these are the actual outlines of the Large and Teenie. They may write down the thickness also.
A completed table with the missing counts filled in.
Highlights of this task:
Kids use some known information to construct new information. They use modeling to figure out what the other sizes may look like and how many of them would fit in a 27-oz or 36-oz package.
It's kinda messy and weird. While the kids can measure whatever lengths of a treat, how do these numbers translate into the mass of each treat?
It's good to work with solid objects instead of just flat polygons when learning similar shapes.
The reveal (Act 3) of something like this is always a lot of fun. Not only the reveal in the count per package, but also how close their outline sketches are to the actual treats when I bring in the Petite, Regular, and Jumbo.
How much does a 36-oz package cost?
Is the Jumbo a shot in the dark? Would kids think to ask me for the size of the dogs? How does this help, if at all?
Rigid Transformations
My 8th graders are learning about rigid transformations. I want to add a bit more complexity to what our book is asking the kids to do. For example, the book is having them reflect a shape mainly across the x-axis or y-axis, or on a rare occasion, reflect it across "the horizontal line that goes through y = 3." Well, right before this chapter, we've been working with writing and graphing linear equations, so I want kids to reflect a shape across any line, including one that may cut through the shape itself.
The book surprisingly has very few examples and exercises with rotations. And from what I can find, all these rotations happen about the origin or about a point coinciding with one of the vertices of the shape. Again, I want kids to be able to rotate a shape about any point, including one that's inside the shape. (I used a playing card — number 7 works well because it's asymmetrical — poked my pencil through it as the center of rotation, and turned the card. I think this helps them see what I keep referring to as the pivot or anchor point.)
Then I give each student this task:
Draw a shape that has between 5 to 8 sides with no curved edges.
Transform your shape through at least 3 rigid transformations of rotation, translation, and reflection — in any order.
On grid paper, give your teacher your complete work on this, including the written directions for the transformations.
On grid paper, give your teacher only the original shape and the written instructions. Your teacher will give this paper to a random classmate to follow your written directions to arrive at the intended location of the final image.
For students who want more challenge, they may ask for a copy that has just the original shape and its final image without the written directions. The task will then be to figure the appropriate transformations that connect the two images.
I really believe that it's good practice to always give kids more than what we believe they can handle. Let kids tell us when it's too much for them — and we find out soon enough. An ounce of struggle on something hard is worth a pound of completion on something easy.
A Tale of Two Gyms
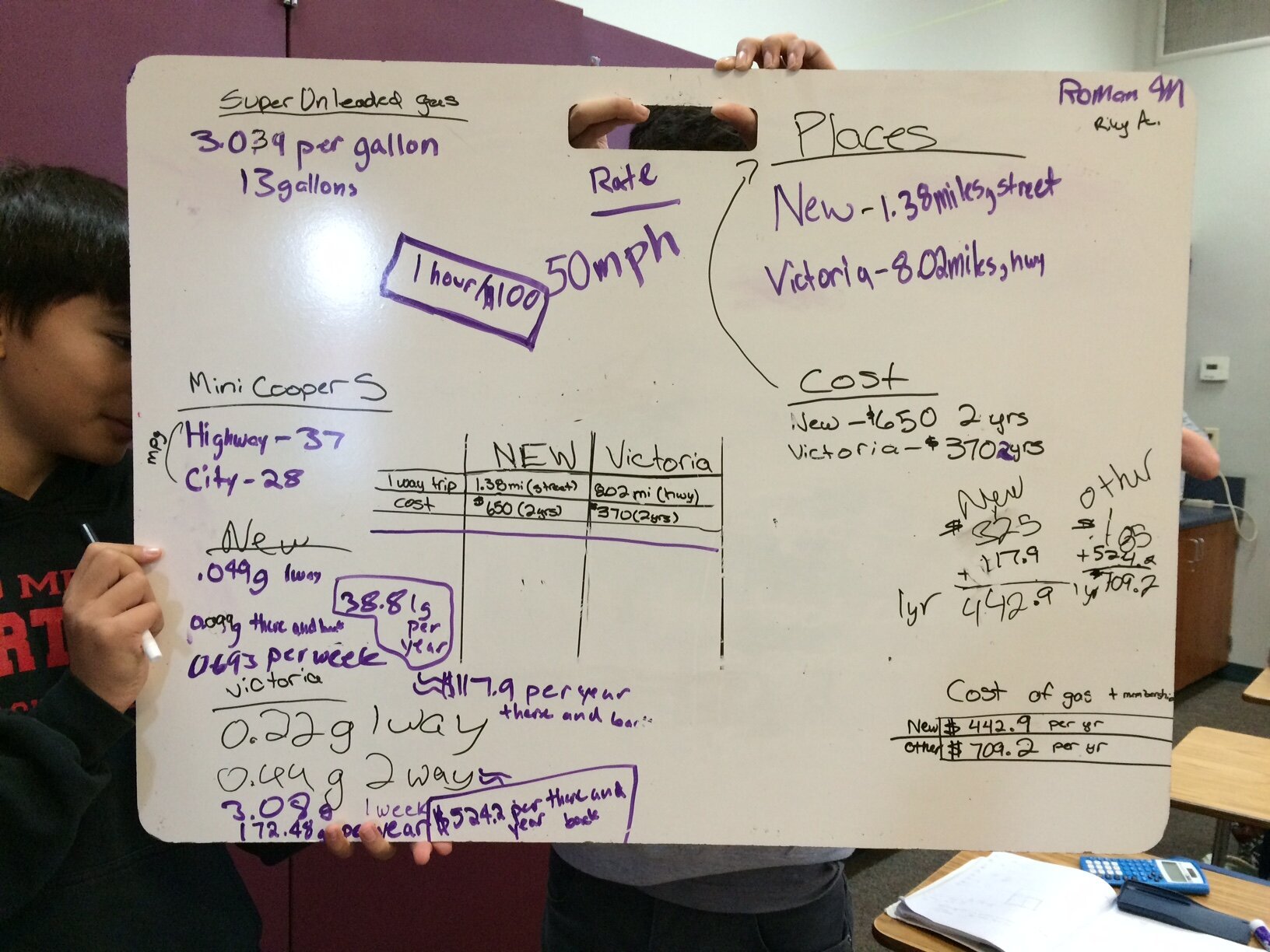
Quick post about a scenario that I was sharing with the kids just to share and how they just took off with it. A brand spanking new 24-Hour Fitness is opening up near me. It's a no-brainer to switch over to this facility because I'll save gas and travel time. However, the 2-year membership that I get from Costco will cost nearly twice as much at the new one. I gave them some information:
8.02 miles one-way to current gym, at mostly highway speed
1.38 miles one-way to new gym, at neighborhood speed
Chevron gasoline currently at $3.039/gallon
$370/2-year membership at current gym
$650/2-year membership at new gym
While it didn't take much to figure out that the new gym costs just 38 cents more per day, but there were enough variables inherent in this scenario that the kids wanted to take a closer look.They asked me questions like:
How often do you go to the gym?
How much mileage does your car get?
How fast do you drive — on highway and around town?
How long does it take you?
I lied about going to the gym 7 days a week, gave them my car model, then told them to look up the rest. But then we wondered about the value of my time driving. How much is my driving time worth? I went on Twitter to ask for help, and Glenn thought I should divide my weekly salary by the hours of weekly driving that I do. The problem is I live pretty close to school, so this rate becomes too high to apply to this situation. For no good reason, I decided to give the kids our school's substitute rate of $115/7 hours, or $16.43/hour. They paired up and went online to gather more information, did a bunch of calculations, and summarized everything on the whiteboard. All in one class period.We should just do this all year: turn a scenario into a question then into a math task. I could take a nap while they chitchat and do all the work.
Four Square and Other Questions
One afternoon during recess I noticed that the Four Square grid at our school had been enlarged. Naturally I yelled out to the kids, "Hey kids, when did they make this larger? I wonder what percent increase this is. What do you think?”
Taking a nanosecond pause from their game, they yelled out their estimates, anywhere from 50% to 95% increase. One kid said, "I love that you're asking us a math question at recess time." I went back out to the playground during my prep with a couple of yardsticks to find the answer to the question I'd posed. When my 6th graders came into class the next period, I told them what I'd wondered about during recess and wanted each one of them to give me an estimate of this percent increase. We walked back out to the Four Square, and I allowed them five minutes to do whatever they needed to get a good estimate.
Once back into the classroom, I asked them to write down their estimate of the percent increase on a small slip of paper. I then asked, "What exactly was I looking for? Percent increase in what? I really didn't say and you didn't ask me to specify either."
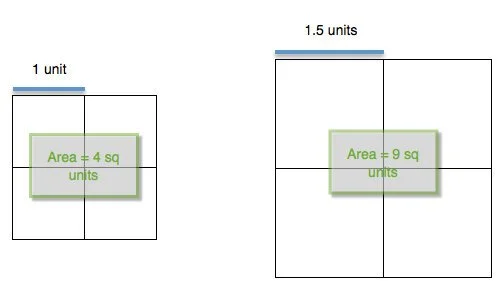
We've been working A LOT with perimeter and area of rectangles, so most of them said that they'd thought I'd meant the percent increase in area. So I told them I did mean area but I was intentionally vague just to see if anyone would ask — and Four Square is so much about occupying the inside space. This question prompted me to ask them more questions about increase in perimeter versus increase in area. I had them draw squares (or rectangles) on grid paper and explore the changes in area when the perimeter is doubled, tripled, or by some x factor. We remind ourselves that area is two-dimensional and why area units are always "squared." I asked them how they would figure out the percent increase in area. They told me I needed to measure the length and width of the old Square (black outlines), then do the same for the new one (white outlines). They also agreed that I could just find the area of 1 square, then multiply this by 4 to get the whole thing. This suggestion prompted me to ask them, "Well, do I need to compare the area of the whole 4-square grid of new to old, or just the area of 1-square of new to old?" So we just drew some squares to show that comparing the areas of just one square each: large to small is 2.25 to 1.0, this is a percent increase of 125%. And comparing the areas of each entire 4-square grid: large to small is 9 to 4, which also yields a 125% increase.
This brief noticing and wondering yielded a fruitful discussion and it was something that was part of their environment, their playground. By the way, the answer is 118% increase in area for the Four Square. The closest written estimate was 115%. Of course this launched us into a brainstorming session of questions that they have about their surroundings. Stuff that we can apply math to answer the questions. I reminded them not to worry about answering the question. Just ask it. Then I couldn't stop them from sharing. (These 6th graders are away at Outdoor School, so I have to wait for them to return next week for us to try and answer some of these questions. They will also be jotting down more questions that may come up during the week.)
How much time does my brother waste in his room for a year?
How many gallons of water do we use if we take 5-minute showers a day?
How much does this cost?
How much power is needed to charge all the devices in the house for a year?
I wonder how many pencil tips I break each year, and if added end-to-end, how long would this be?
What is the average amount of money each teacher at our school spends on supplies in a school year
How many eggs does a chicken lay in United Kingdom?
How much pollution does the average car put into the air monthly?
How much time do the students in this class spend on YouTube in a month?
How much time do we spend on homework during the school year?
How much money does our school lose when students are absent?
How long does my hair grow in a month?
I always wondered how much bigger is the big basketball hoop compared to the small one.
How many pounds of food do kids waste in the cafeteria in a month?
How much gas does my mom burn while she is driving?
I wonder how much gasoline our 3 school buses use each year.
How many "perimeters" do we do in a year in PE?
How much money does Mrs. Nguyen spend on Oregon Ducks' games?...
And this one breaks my heart.
How long would it take to end poverty?
Driving Them Nuts
I'm proud of my students. I'm proud of what we do in room 15. My classroom. My home away from home for the last 11 years. These bopping teenagers, sullen one minute bubbly the next, hormonal but invincible. They don't all love math like I do. (Not everyone loves college football, but we get along.)
What is happening in room 15 is the loud and proud math culture that we have set in place. We build it from day one — then we continue to do, say, and write stuff to sustain and strengthen the culture because we know our behaviors are our best evidence that this culture exists.
Here's one piece of that evidence:
Her frustration resulted in her loving the problem. Her last sentence is an enormous celebration of how much we honor the process of problem solving. Her classmates had their own reflections — short snippets of how they engaged in the problem.
They worked hard on the problem because it was driving them nuts. It's not unusual to hear kids blurt out, "This problem is making me crazy!" Or, "I won't be able to think about anything else until I get this!" Now, they've owned it. This isn't about a letter grade any more; and it certainly isn't about me.
This was the problem they'd worked on.
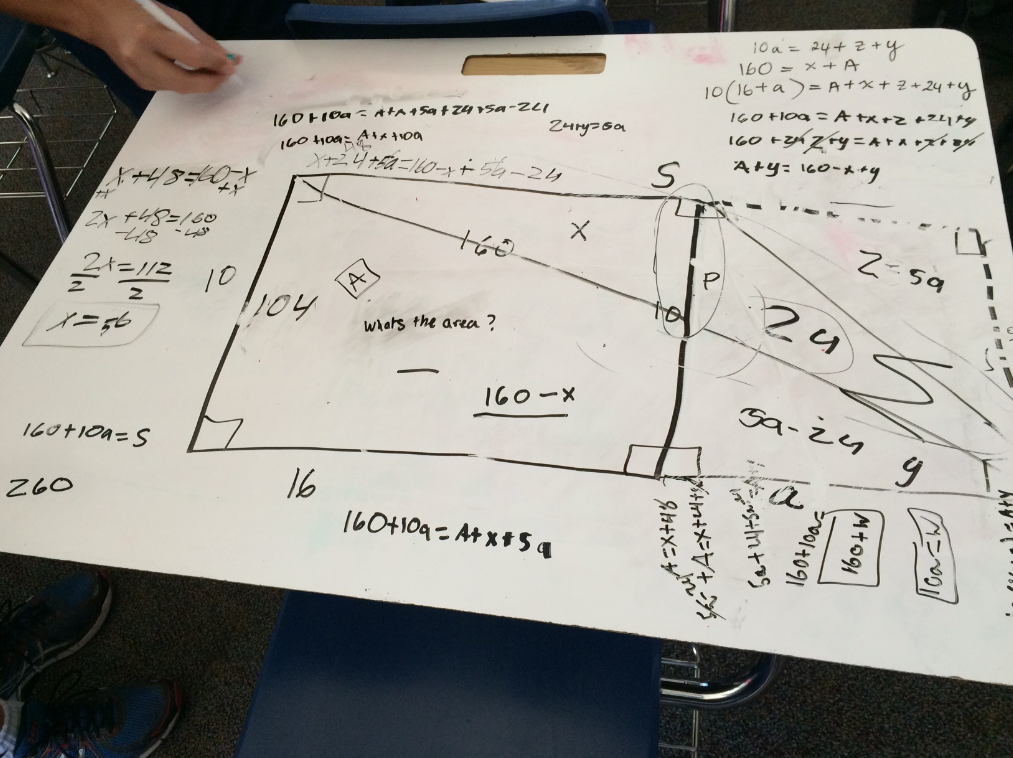
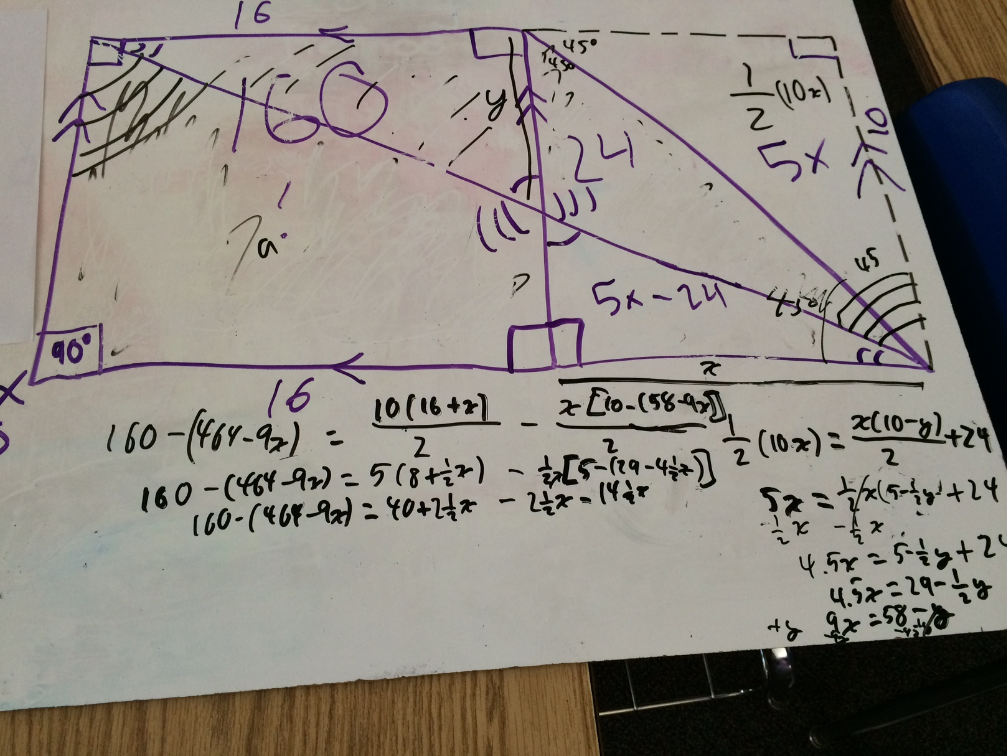
The Missing Area
A 10 by 16 rectangle is attached to a triangle as shown below. If the purple section is 24 square units, then what is the area of the yellow section of the rectangle?
John Golden, GeoGebra extraordinaire, created an animated gif of this problem.
Mike Lawler solved this problem using similar triangles.
A Simpler Solution
I'm guessing this was about 5 years ago. I was at an all-day workshop when a high school math teacher, sitting next to me, asked about the PoW (from mathforum.org) that I had assigned to my students. I happened to have an extra copy in my backpack and gave it to her.
Dad's Cookies [Problem #2959]
Dad bakes some cookies. He eats one hot out of the oven and leaves the rest on the counter to cool. He goes outside to read.
Dave comes into the kitchen and finds the cookies. Since he is hungry, he eats half a dozen of them.
Then Kate wanders by, feeling rather hungry as well. She eats half as many as Dave did.
Jim and Eileen walk through next, each of them eats one third of the remaining cookies.
Hollis comes into the kitchen and eats half of the cookies that are left on the counter.
Last of all, Mom eats just one cookie.
Dad comes back inside, ready to pig out. "Hey!" he exclaims, "There is only one cookie left!"
How many cookies did Dad bake in all?
Maybe you'd like to work on this problem before reading on.
…
…
…
…
…
…
The teacher started solving the problem. She was really into it, so much so that I felt she'd ignored much of what our presenter was presenting at the time. She ran out of paper and grabbed some more. She looked up from her papers at one point and said something that I interpreted as I-know-this-problem-is-not-that-hard-but-what-the-fuck.
It was now morning break.
She worked on it some more.
By lunch time, she asked, "Okay, how do you solve this?" I read the problem again and drew some boxes on top of the paper that she'd written on. (Inside the green.)
She knew I'd solved the problem with a few simple sketches because she understood the drawings and what they represented. I just really appreciated her perseverance.
I share this with you because a few nights ago I was at our local Math Teachers' Circle where Joshua Zucker led us through some fantastic activities with Zome models. We were asked for the volume of various polyhedrons relative to one another. Our group really struggled on one of the shapes. We used formulas and equations only to get completely befuddled, and our work ended up looking like one of the papers above.
Over the years I've heard a few students tell me, "Mrs. Nguyen, my uncle is an engineer, and he can't help me with the PoW." Substitute uncle with another grown-up family member. Substitute engineer with another profession, including math teacher. I remember getting a note from one of my student's tutor letting me know that I shouldn't be giving 6th graders problems that he himself cannot solve. (The student's parent fired him upon learning this.)
I like to think that my love of problem solving will rub off on my kids. I hope they will love the power of drawing rectangles as much I do.
Multiplication: Finding the Greatest Product
From a set of 1 through 9 playing cards, I draw five cards and get cards showing 8, 4, 2, 7, and 5. I ask my 6th graders to make a 3-digit number and a 2-digit number that would yield the greatest product. I add, "But do not complete the multiplication — meaning do not figure out the answer. I just want you to think about place value and multiplication."
I ask for volunteers who feel confident about their two numbers to share. This question brings out more than a few confident thinkers — each was so confident that he/she had the greatest product. (I'm noting here that I wasn't entirely sure what what the largest product would be. After this lesson, I asked some math teachers this question, and I appreciate the three teachers who shared. None of them gave the correct answer.)
I say, "Well, this is quite lovely, but y'all can't be right." I ask everyone to look at the seven "confident" submissions and see if they could reason that one yields a greater product than another, then perhaps we might narrow this list down a bit.
Someone sees "easily" that #7 is greater than #6. The class agrees.
Someone says #7 is greater than #1 because of "doubling." She says, "I know this from our math talk. Doubling and halving. Look at #1. If I take half of 875, I get about 430. If I double 42, I get 84. Both of these numbers [430 and 84] are smaller than what are in #7. So I'm confident #7 is greater than #1."
Someone else says #5 is greater than #4 because of rounding, "Eight hundred something times 70 is greater than eight hundred something times 50. The effect of multiplying by 800 is much more."
Someone says, "Number 2 is also greater than #1 because of place value. I mean the top numbers are almost the same, but #2 has twelve more groups of 872."
But the only one that the class unanimously agrees on to eliminate is #6. Then I ask them to take 30 seconds to quietly examine the remaining six and put a star next to the one that they believe yield the greatest product. These are their votes.
I tell them that clearly this is a tough thing to think about because we've had a lot of discussion yet many possibilities still remain. And that's okay -- that's why we're doing this. We've been doing enough multiplication of 2-digit by 2-digit during math talks that it's time we tackle something more challenging. So #3 gets the most votes.
I then punch the numbers into the calculator, and the kids are very excited to see what comes up after each time that I hit the ENTER key. Cheers and groans can be heard from around the room. Turns out #3 does has the greatest product (63,150) out of the ones shown.
Ah, but then someone suggests 752 times 84. I punch it into the calculator and everyone gasps. It has a product of 63,168.
Their little heads are exploding.
I give them a new set of five for homework: 2, 3, 5, 6, and 9. They are to go home and figure out the largest product from 3-digit by 2-digit multiplication. They come back with 652 times 93.
The next day, we try another set: 3, 4, 5, 8, and 9. We get the greatest product by doing 853 times 94. There is a lot — as much if not more than the day before — of sharing and arguing and reasoning about multiplication and place value.
Many of them see a pattern in the arrangement of the digits and are eager to share. They've agreed on this placement.
Then we talk about making sure we know we've looked at all the possible configurations. They agree that the greatest digit has to either be in the hundreds place of the 3-digit number or in the tens place of the 2-digit number. We try a simple set of numbers 1 through 5, and we agree that there are just 9 possible candidates that we need to test. The same placement holds.
Then we draw generic rectangles to remind us that we've just been looking for two dimensions that would give us the largest area.
I remember saying to the class, more than once, that this is tough to think about. To which Harley, sitting in the front row, says, "But it's like we're playing a game. It's fun."
Two Pizzas and Five People
I'm thinking a lot about how my 6th graders responded to a pre-lesson task in "Interpreting Multiplication and Division" — a lesson from Mathematics Assessment Project (MAP) .
MAP lessons begin with a set structure:
Before the lesson, students work individually on a task designed to reveal their current levels of understanding. You review their scripts and write questions to help them improve their work.
I gave the students this pre-lesson task for homework, and 57 students completed the task.
I'm sharing students' responses to question 2 (of 4) only because there's already a lot here to process. I'm grouping the kids' calculations and answers based on their diagrams.
Each pizza is cut into fifths.
About 44% (25/57) of the kids split the pizzas into fifths. I think I would have done the same, and my hand-drawn fifths would only be slightly less sloppy than theirs. The answer of 2 must mean 2 slices, and that makes sense when we see 10 slices total. The answer 10 might be a reflection of the completed example in the first row. "P divided by 5 x 2 or 5 divided by P x 2" suggests that division is commutative, and P here must mean pizza.
Each pizza is cut into eighths.
Next to cutting a circle into fourths, cutting into eighths is pretty easy and straightforward.
Each pizza is cut into tenths.
I'm a little bit surprised to see tenths because it's tedious to sketch them in, but then ten is a nice round number. The answer 20, like before, might be a mimic of the completed example in the first row.
Each pizza is cut into fourths.
I'm thinking the student sketched the diagram to illustrate that the pizzas get cut into some number of pieces — the fourths are out of convenience. The larger number 5 divided by the smaller number 2 is not surprising.
Each pizza is cut into sixths.
It's easier to divide a circle by hand into even sections, even though the calculations do not show 6 or 12.
Each pizza is cut into fifths, vertically.
Oy. I need to introduce these 3 students to rectangular pizzas. :)
Five people? Here, five slices.
Mom and Dad are bigger people, so they should get the larger slices. This seems fair. We just need to examine the commutative property more closely.
Circles drawn, but uncut.
I'm wondering about the calculation of 5 divided by 2.
Only one pizza drawn, cut into fifths.
Twenty percent fits with the diagram, if each person is getting one of the five slices. The 100 in the calculation might be due to the student thinking about percentage.
Only one pizza drawn, cut into tenths, but like this.
I wonder if the student has forgotten what the question is asking for because his/her focus has now shifted to the diagram.
Each rectangular pizza is cut into fifths.
Three kids after my own heart.
Five portions set out, each with pizza sticks.
I wonder where the 10 comes from in his calculation.
Five plates set out, each plate with pizza slices.
Kids don't always know what we mean by "draw a picture" or "sketch a diagram." This student has already portioned out the slices.
What diagrams and calculations would you expect to see for question 3?
There's important work ahead for us. The kids have been working on matching calculation, diagram, and problem cards. They're thinking and talking to one another. I have a lot of questions to ask them, and hopefully they'll come up with questions of their own as they try to make sense of it all. If I were just looking for the answer of 2/5 or 0.4, then only 12 of the 57 papers had this answer. But I saw more "correct" answers that may not necessarily match the key. We starve ourselves of kids' thinking and reasoning if we only give multiple-choice tests or seek only for the answer.
That's why Max Ray wants to remind us of why 2 > 4.