Two Lessons: Frog Leap and Beach Ball

I call it Frog Leap but you may know this common game as Stepping Stones or Traffic Jam. NRICH has a nice interactive applet.

The challenge is for the 3 boys and 3 girls to switch places in the FEWEST moves possible. A legal "move" is each person can jump onto an adjacent empty space or jump over another player onto an empty space. (Two people just switching places is not okay.)

I placed 7 pieces of paper on the floor and asked six kids to come up and "act it out." They were stuck a bunch of times despite a lot of input from the audience.

Once they got the idea of the game, I let them explore it individually using small cubes. When they thought they had found the fewest moves, they wrote down their answer and called me over to check—this, of course, was so no one would share the answer aloud. If they had the correct answer, I asked them to try with 8 cubes, 4 on each side.

After about 15 minutes of individual work time, I randomly paired kids up. I asked them to track the moves, meaning which cube went to which position.

The kids already knew that, eventually, we would want to figure out the fewest moves for any number of people. Two students found the correct equation after testing for 12 people, six on either side. We tracked the moves together as a class so that we could see the cool symmetry in them.

Instead of looking at the total number of people, one could also just work with pairs of people. The two students who figured out the equation regarded each pair as a step number — so step 3 meant 3 pairs of people, or 6 people — and their equation as:

fewest moves = (step number)^2 + 2(step number)

When we do these types of problems, it's really no big deal to me if the kids don't arrive at the general rule, I think the process itself is more important. But I try to expose them to a lot of problem-solving, and they are getting better at it. And they are persevering.

We're doing simple constructions by hand in geometry. So far, they've learned how to copy a segment and an angle, along with how to bisect a segment and an angle. But nothing too exciting could come out of this. I'm now looking for geometric theorems that kids could construct from scratch, that way when we're done, something exciting awaits us!

One of my favorite sites is Math Fun Facts by Professor Francis Su of Harvey Mudd College. I geekishly introduced myself to Dr. Su at a UCLA Math Festival 4 years ago — in my world, he is a rock star and I'm just a big fan!

Su posts a theorem he calls Pizza Slices:

Take a pizza and pick an arbitrary point in it. Suppose you cut the pizza into 8 slices by cutting at 45 degree angles through that point, and color the alternate pieces red and green.

Surprising theorem: the total area of the red slices and the total area of the green slices will always be the same!

And that's what my geometry kids did! They needed to construct perpendicular chords and bisected each of these 90-degree angles to get the 45-degree angles. My kids called them beach balls.

Even though the proof for this theorem requires calculus and polar coordinates, it doesn't mean we can't know about it and appreciate this fun fact. 

[09/28/12: Joshua Zucker wrote:]

There's a much simpler proof of the "pizza theorem", as your beach ball problem is often called. Take a look at Stan Wagon's dissection proof, shown at http://en.wikipedia.org/wiki/Pizza_theorem for example. No need for calculus or polar coordinates! Just a pair of scissors. Well, and some logic explaining why the pieces that look congruent really are.

[09/29/12: Suzanne Alejandre wrote:]

Fawn, you might find this blogpost that I wrote on Traffic Jam interesting:

http://mathforum.org/blogs/suzanne/2011/08/14/whats-in-a-touch/

I find it fascinating to watch students move between concrete manipulatives, virtual manipulatives, their bodies as manipulatives and then paper/pencil representations of the mathematics. I think this particular activity whether it's called Leap Frog or Traffic Jam or ? is a perfect one to help students practice perseverance as you have noted.

A Lazy Teacher's Version of Block Game

I love the "Block" game that my colleague Erin has shared with me. Erin found it at Maria Anderson's post. It looked familiar, turned out it was one of Elizabeth's #made4math posts.

There's just this one BIG problem: I dread making games that require a bunch of little game pieces!!

Erin must have spent hours typing up the 36 math expressions for the distributive game, wrote the 36 answers on the back, made 18 copies — for 36 kids to play in pairs — and cut each copy into 36 little game pieces. I felt bad using them because I didn't help at all.

Whenever I borrow stuff I'm extra careful with it, so I kept reminding my kids to be gentle with the pieces, to not lose any of them, to not write on them, and don't even breathe on them!

Because the algebra kids really liked the game, I thought, Okay, I'm going to make one for order-of-operations for my 6th graders! I lasted all of five minutes.

Then an idea popped into my head that requires NO GAME PIECES AT ALL!!

I made two changes:

1. Instead of a blank 4x9-grid game board, I number the spaces from 1 to 36.

2. Instead of typing up 36 questions and 36 answers (photocopied back-to-back) and cutting them out, I use KUTA to generate a worksheet with 36 questions — takes 1 minute. KUTA also automatically generates the answers. I print the questions and answers back-to-back.

So, this would be all that is needed for two players:

• 1 game board

• 2 worksheets (36 questions in front, 36 answers in back) — one for each person

• 2 different game markers

You can put the game boards and worksheets into plastic sleeves — or laminate them — to protect and re-use them. I'm just going to protect the game boards but leave the worksheets as consumables, this way kids can write on them to do their math work.

The game is similar to tic-tac-toe 4-in-a-row. Maria's directions in pdf.

Yes, kids can cheat in this game because the answers are in the back of the worksheet or in the back of each game piece. But I make it clear that each person needs to show his work to the opponent.

Cheaters cheat themselves. I don't care.

Math Teachers' Circle

Last Monday morning I was on a SuperShuttle from SFO to the Creekside Inn. But I was running a little late, so the driver took me straight to the American Institute of Mathematics (AIM). I was expecting a tall building with lots of glass windows — instead the driver stopped here.

I was at AIM to attend a one-week workshop on How to Run a Math Teachers’ Circle. I stumbled upon this opportunity simply by doing a search for a Circle that I could be a participant in. But there wasn't one in my area that I knew of, hence my always-ambitious-but-never-know-what-the-hell-I'm-getting-myself-into evil twin said, Why don't you start one?

I asked Erin, my next-door math colleague, to join me. She and I fulfilled the requirement for "two middle school math teachers" — we just needed to find "two mathematicians and one administrator or organizer" to make a team of five.

I contacted Brianna Donaldson, AIM's Director of Special Projects, to help us round out the team. Within the week, she hooked us up with Nate and Hala, both are math professors at Cal Lutheran. We still needed a fifth member, so I asked Melissa, another math colleague (there are only 3 of us at our junior high) — she graciously got on board.

Needless to say I was thrilled to hear that our team was chosen among many (like hundreds of thousands of teams) to receive full funding to participate in this workshop.Below is a summary of my week in beautiful Palo Alto, California. (For some reason it's easier for me to write in present tense when I recount a story — maybe it's an ELD or ESL thing.)

Monday

I meet the other two members of our team for the first time, Nate and Hala. I've seen their pictures online, and they look the same — thank God!There are six teams: 2 from Texas, 1 Kansas, 1 New York (Rochester), and 2 California.

Josh Zucker appears first on the agenda, "Introduction to Problem Solving." I've always wanted to meet Josh — his name appears on most of the cool math problems that I first encountered at the Julia Robinson Mathematics Festival in Los Angeles. Turns out he's the director.

He facilitates this classic problem:

The numbers 1 through 100 are written on the board. You choose any two numbers x and yand erase them, writing xy + x + y in their place. You continue to do this until one number remains. What are the possible values for that remaining number?

I just want to post the problems here without further discussions on them so that you — the thinker, the mathematician, the teacher, the student, the problem solver — get to struggle with the problem and construct meaning for yourself.

There are three things that happen consistently each day, so I'll just mention them once here:

1. We get two hours (TWO HOURS!!) for lunch as the nearby restaurants are about a 15-minute walk away.

2. After lunch, we work within our group on logistics and fundraising to run our own math circle.

3. "Happy Hour" greets us at the end of each session, if we wish to stay.

Tuesday

Tatiana Shubin is a math professor at San Jose State University; she presents Grid Power. I've always required my students to use quadrille-ruled composition notebooks to take notes and such, but after hearing Tatiana speak, I want my kiddos to do ALL their math work on grid paper!

Tatiana gives us this delightful problem:

How many squares are there in a 7 x 7 square?

Paul Zeitz introduces us to "Mathematical Games." He's a math professor at the University of San Francisco and is taking a sabbatical this year. I've ALWAYS wanted to buy the book The Art and Craft of Problem Solving — lo and behold, Paul is the author! But Paul doesn't once mention his book. (I made the connection after the workshop was over.) Instead he recommends James Tanton's Solve This. I need these books.

Two of the games we work on:

Takeaway. A set of 16 pennies is placed on the table. Two players take turns removing pennies. At each turn, a player must remove between 1 and 4 pennies (inclusive). The winner is the last player to make a legal move.

Puppies and Kittens, aka Wythoff's Nim. We start with a pile of kittens and puppies. Two players take turns; a legal move is removing any number of puppies or any number of kittens or an equal number of both puppies and kittens. The winner is the last player to make a legal move.

I really like how Paul keeps track of winning/losing moves as oasis/desert points on a horizontal line. So with the two variables like in Puppies and Kittens, we use a coordinate plane instead to record.

Wednesday

Diana White is a math professor at the University of Colorado Denver. Diana facilitates us through the Exploding Dots problem. (James Tanton owns the dots.)

Say you have a machine that holds ping pong balls. If you put three balls in the far right slot, they'll explode and two balls will move one space left into the next slot. Like this:

This happens with any set of three balls in one slot, therefore the explosion continues until there are fewer than three balls per slot. Thus, starting with 9 ping pong balls, the result looks like this:

Tom Davis is a retired math professor; he walks us through Conway's Rational Tangles. I don't even know how to begin to explain and illustrate this problem. It requires four students and two long ropes — each student holding one end of a rope. The task is to do two (and only two) commands of "twist" and "rotate" to tangle up the ropes — the challenge then is to untangle the ropes in a systematic way that involves arithmetic with positive and negative fractions. Okay, my explanation is as clear as mud.

The point is it is a wonderful activity that kids and teachers will absolutely love to get their hands on, literally. The other point is I'm better than you because I have the two ropes. See?

Thursday

Paul Zeitz is back this morning with "How to Gamble If You Must." We play a few dice games, then we work on Two Lottery Tickets:

It costs a consumer $1 to buy a Klopstockia lottery ticket. The buyer then scratches the ticket to see the prize. Compute, to the nearest penny, the expected profit that the state of Klopstockia makes per ticket sold, given the following scenarios for prizes awarded. (The state will make a profit if the expected value to the lottery ticket is less than $1.)

Friday

There is no math activity on our last day. Each team has 10 minutes to present the how/what/where/when of their own future Math Teachers' Circle. We each get a T-shirt and our team pictures taken. We bid farewell at noon.

I'm grateful to everyone who made this workshop possible. And I love my team!! So I lied about us being chosen among hundreds of thousands. I had never drank so much wine in one week. I took two wine corks home to practice a trick Josh had taught us. Please consider joining a Math Teachers' Circle in your area. Our team leads the Thousand Oaks MTC and would love to have you. (I'm working on our website.) We owe it to our students to make math engaging and accessible.

Last Math Lessons

On the first day of school, I promised all my students that I'd do my best to make math relevant and challenging. I also promised to never waste their time, therefore they could expect to do math every day in my class, including the last day of class.

I did not promise them that math would be fun because doing math is always fun to me. I gave out math puzzles at my kids' birthday parties when they were younger, also at a baby shower that I gave, and of course at my own wedding.

Math 6

I called this lesson How Many Regions? (Adapted from AIMS)

I gave each student a piece of 4-by-4-inch paper and a handful of 6-inch long thin strips of construction paper. Each strip placed on the square paper would represent a "cut."

Question: What is the maximum number of regions that you can divide the square into using n number of "cuts"?

We did the first two cuts together as a class, and each student kept track of the data in their journal.

Because the goal was to get the maximum number of regions from the cuts, the kids learned quickly that the cuts needed to intersect. For example, two non-intersecting cuts created only 3 regions. A kid yelled out, "Parallel cuts!" Gotta forgive kids who blurt out academic language!

This class has been working with a pattern worksheet almost every Monday in my class, so they know to look for a recursive rule and try to find the equation for the nth term. Recursively, they saw the pattern, so it didn't take long for them to figure out that for any n (cuts), the maximum number of regions is the sum of n and the number of regions from the previous n.

With 30 seconds left of class, I told them my gift to them was to try and figure out the equation. Matt asked, "Can I email you then over the summer?"

Algebra 1

Our 8th graders' last day of classes was yesterday (Wednesday). They'll show up this evening for their promotional ceremony, dressed to the hilt.

I needed a quick one-period lesson, so I had them make 2012 Clocks. This is a common assignment: using all 4 digits in "2012" and each digit only once, they had to create expressions that would equal to the hours of 1 through 12 on a clock.

Geometry

I've seen different versions of this problem; the first time I worked on it was when it involved 3,000 bananas and 1 camel traveling 1,000 miles. I know there's a perfectly good strategy called "solve a simpler problem," but we could also start with a simpler one!

I gave my kids Desert Crossing, also from AIMS:

You live in a desert oasis and grow miniature watermelons that are worth a great deal of money, if you can get them to the market 15 kilometers away across the desert. Your harvest this year is 45 melons, but you have no way to get them to the market, except to carry them across the desert. You have a backpack that holds up to 15 melons, the maximum number that you can carry at a time. To walk across the desert, you need a certain amount of fluid and nourishment that is supplied by the melons you carry. For each kilometer you walk (in either direction), one melon must be eaten.Your challenge is to find a way to get as many melons as possible to market.

As I type this, Slater does not know that I will be awarding him the Math Excellence Award at the Promotional Ceremony this evening.

Here is Slater's work that shows one way to get the correct answer of 8 watermelons.

I did this a few weeks ago and forgot all about it; so here's a little blurb on it.Each student quickly constructed these two prisms from two same size papers.

(Dan Meyer folded them into cylinders.)

Question: Pretend the two prisms have bottoms on them, which one holds more popcorn? Take a look... Okay, grab the one you think holds more, or grab both if you think they're both equal.

And this was how they grabbed:

Then they measured and calculated the volume.

My favorite student comment: The tallness didn't make up for the fatness.

Estimating volume is a funny thing.

Visualizing Volume is Tricky!

This was one of those lessons that I think I gained a lot more than my 6th graders did. It was meant as a one-period activity, but I kept going off on different tangents and brought the students along for the ride.

Over a month ago Andrew Stadel tweeted me a picture that he took of a William Sonoma display of their cupcake mixes. I was at our local mall last Sunday and saw a similar display. We both thought about buying the mixes to make cupcakes for our kids, but it was $15 a can, and we'd need three, so the poor teachers said no can do.

I projected the images above and asked the kids to give me a guess of how many dozens or how many individual cupcakes can the large container make when the small [real] container can make 1 dozen or 12 cupcakes.

Their guesses were all over the place, ranging from 47 to 994 cupcakes. (We were very careful whether the submitted guesses were in "dozens"or in "individual cupcakes.")

So I did the only thing I knew. I replicated the two cans so the kids could see them physically in the room instead of just on a still photo. Granted the large "can" made from butcher paper was pretty awful.

But, before I asked for another guess at the number of cupcakes, it occurred to me that I wanted to know if kids were better at guessing one and two-dimensional items.

Question 1: How many times taller is one segment than the other?

The two segments below are proportional to the heights of the two cans.

Their estimates:

Question 2: How many times longer is one circumference than the other?

The two circles are proportional to the cans' tops/bottoms.

Their estimates:

Question 3: How many times larger is the area of one circle than the other?

The two circles are proportional to the cans' tops/bottoms.

Their estimates:

Then, I let the kids — row by row — come up to get a visual check at the paper replicas of the cans. But they may not manipulate the models because I was more interested in seeing the difference between their guesses of the still photo and the physical models.

Their estimates:

If I wrote this post as Dan's 3-Act Lesson, then it was time for Act 2: figure out the volumes of the two cans using their measurements. (Yes, I carry a measuring tape wherever I go now.)

I tried to show the kids equivalent measures whenever possible. We worked a lot with centimeter cubes this year, so this was a rare time that we measured in cubic inches.

And here are some estimates from grown-ups who only saw the left image at the top of post:

(Got more guesses after I printed this: 1,000, 182, 600, 576.)

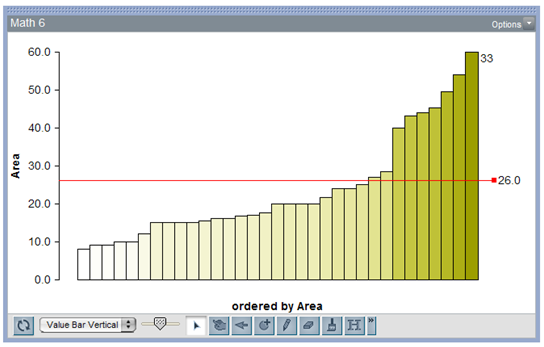
The straight lines [heights] seemed easiest to estimate. It got a little bit tougher when these lines bend into circles [circumferences] — and there was a large number of over-estimates here. I thought area estimates were pretty good, average of all 33 student guesses was 28.3 (calculated was 26).

The volume estimates, from kids and adults, remained well under the calculated numbers. I don't know what to make of all this. But I kept wondering: Are boys or girls better at making volume estimates? (From my small sample of 33 students, the girls were closer.) How about science teachers? The 3D models helped overall; and I bet if I let the kids do everything but measure the cans, their numbers would be closer. Interestingly, at one point I'd placed the smaller can inside the larger can, and kids who stood nearby kinda gasped. One said, "Oh, you can fit a lot inside."

Thank you, once again, to Andrew for sending me that tweet that started all this! He did a wonderful presentation of 3-Act Lessons to his staff.

Area of a Circle

After finding the formula for the circumference of a circle, my 6th graders were ready to work on finding the area of a circle.

I asked them to draw a circle on notebook paper, any size, but not too small. Then I gave each a centimeter cube to trace one face onto their paper to remind them how much the area of one square centimeter covered. (You can see it drawn on top right pic below.)

Question 1: Give me a guess — only by looking — what is the area of your circle, in square centimeters? Please write that number on your paper, label it "guess."

Question 2: Now use whatever tools you need, give me a better answer. I know some of you already know the formula for the area of a circle, but you may not use it unless you can tell me where it came from. (No one even tried.)

I can't tell you how happy I was to see all the different ways the the kids had tried to approximate area. Their perseverance humbled me. A few students drew triangles, knew to use "base times height divided by two," but erroneously used radius as height.

Last week I was reading Mimi's post about estimating area of circles, and Sue VanHattum reminded me of the rectangle model in her comment.

I had the kids fold their circles like this.

They cut out the pieces — turning every other piece 180 degrees — and glued them together. Cristian said, "First we had a circle, then triangles, then a rectangle. That's crazy!"

Never once did I answer any of the questions. I just asked them. I began with, "What is the area of this rectangle or parallelogram?" Step by step, as a class, the kids walked this equation all the way to Area = pi x radius^2.

This morning, two days after the activity, I did a My Favorite No to see if they remembered: 31 out of 33 students got the correct circumference formula; 24 of 33 got the correct area formula. Bonus if they showed me how the rectangle model helped explain the area of a circle.

Follow Up on Friday Bubbles

My 6th graders had a blast last Friday blowing bubbles.

Upon their return on Monday, I asked for ten groups to volunteer just one set of their circumference and diameter numbers. Then I asked, "What is the relationship between these numbers?" Some quiet mumbling, then just quiet. I asked again, "I have these 10 sets of numbers. What should I do with each set of numbers to see if there's a relationship between them? I want you to use your calculator to do something with these two numbers and find out for me."

They were busy punching in numbers. After a few minutes...

Me: What are you punching into your calculator?

Matt: I'm dividing the numbers.

Me: Why divide? Why not add or subtract? Or multiply the numbers?

Matt: Adding and subtracting don't tell you anything. Just doesn't make sense.

Sophia: The circumference is always bigger than the diameter. So I think I want to know how many times it's bigger.

Me: Class, do you agree that we should divide circumference by diameter? (Lots of nods around the room.)

While they continued with their own bubble numbers, I filled in the "relationship" column for the 10 volunteered sets from earlier.

They were skeptical — didn't know what to make of the "relationship" column. I said, "I think measuring a bubble imprint with a string is not easy. It was fun to blow bubbles, for sure. But what about it that may have affected how your numbers came out?"

Their answers:

The bubbles were sometimes oval shaped.

Hard to keep the string perfect.

It can get messy!

Maybe some people didn't measure the widest part.

Maybe they measured in centimeters for one part and inches for another.

It was so much fun! (I can always count on a random answer.)

I said, "Because our bubble numbers could use some help. Let's do a clean run through this again, this time using paper and pencil."

I asked them to draw two to three different sized circles on notebook paper — measure the diameter and circumference of each one. I showed them how to "walk" the string around the circle for better accuracy — press and let go, press and let go... They knew that if they started from one end of a diameter, walked the string around the circle, to the other end of the diameter, then they just needed to multiply this by two to get the circumference.

I asked them to find the "relationship" number again for each circle.

The paper in top row, left, reads: All of them are around 3, which is close to pi. Other papers didn't include observations or conjectures, and a few wrote they weren't so sure. But when we shared ALL the "relationship" numbers that the class had — over 60 of them as each student did at least 2 circles — and they were pretty well convinced that the diameter was "about 3 times longer" than the diameter!

I showed them this very short video to reflect the simple work that we did.

Next up, we are going to find the AREA of a circle!!!!!!!

Dissecting Polygons

I appreciate any math lesson where I give the students minimal instruction, yet the lesson is rich in content and it gets kids to do math. (I'm learning to do more and more of not doing much.)

Each student got two pieces of grid paper.

Part 1

In portrait orientation, fold paper in half vertically and approximately into thirds horizontally. Unfold paper to see the six sections created by the folds. Repeat with the other paper. Number the two papers from 1 to 6, like this.

Then I gave each student a ruler and these instructions:

In section 1 of your paper, draw a parallelogram. Find a way to cut your parallelogram into pieces that you can rearrange to form a rectangle. (Here I clarified what I meant: all the cut pieces from the original figure must be put together again to form the requested figure without gaps or overlaps — like a jigsaw puzzle.)

I gave students more graph paper and encouraged them to redraw the parallelogram so they could actually make the cut(s) using scissors. But for this first question, the kids were able to just make a "visual" cut — showing it as a dashed segment — and the requested figure was drawn in the section to the right of the original figure, something like this. (Two students' original parallelograms were rectangles, and that was perfectly okay.)

When everyone understood the directions, I gave out the next five challenges — all as oral instructions.

In section 2: Start with a right triangle. Cut it into pieces that will form a rectangle.

In section 3: Start with a scalene, non-right triangle. Cut it into pieces that will form a parallelogram.

In section 4: Start with a scalene, non-right triangle. Cut it into pieces that will form a rectangle.

In section 5: Start with a trapezoid. Cut it into pieces that will form a rectangle.

And in section 6: Start with a trapezoid. Cut it into pieces that will form a triangle. (See if you can do this with a single cut.)

The kids were really engrossed in this activity!

They were doing a lot of drawing and re-drawing; they were cutting each polygon into pieces and manipulating them.

What they said during the activity:

What the... Oh, I gotcha.

No cheating, J. (to which J. responded with "I am ahead of you, dude!")

I have number six done!

Yeah, but did you do it with one cut?

Z. is on number six because he skipped 4 and 5.

I'm still working on number three...Why can't I draw a scalene triangle?! UGH!!

Can I flip a piece? (I didn't think of this, so it certainly wasn't part of my instruction. We discussed and agreed that you may NOT flip a piece over. Kids started labeling their pieces or coloring one side so they wouldn't accidentally flip them.)

I later asked them to add color to the different edges of the polygons/cut pieces with different colors to make it easier for someone to follow how the pieces had translated after the cut.

No one had finished all 6 tasks; most were working on task 4, so I asked them to spend about 30 minutes more on it for homework.

Tomorrow I'll check their progress on Part 1. I'll ask kids to come up and share their ways of dissecting the polygons. Then we'll move on to Part 2. But I'll be sure to collect their work on Part 1 first because I don't want them to look back at Part 1 to do Part 2 — I'm just mean that way.

Part 2

Sort of like the reverse of Part 1. In Part 1, students were asked to dissect various shapes and rearrange their pieces to form mostly rectangles. While in Part 2, students will begin with rectangles and dissect each one to form these shapes: 1) an isosceles triangle, 2) a right triangle, 3) a scalene triangle, 4) a non-rectangular parallelogram and 5) a trapezoid.

I'm so excited for tomorrow because this went so well today! I love math and I love my students!!

Friday Bubbles

This activity is a lot of fun for 6th graders to discover for themselves the relationship between diameter and circumference.

Given a small container of bubble solution, the student pours a little of it onto his/her desk and use a straw to blow a bubble. When a bubble pops, it leaves enough of an imprint on the desk for the student to measure its diameter and circumference with a string. Students continue to blow different-sized bubbles and record their measurements.

Mix these three ingredients together well for a perfect bubble solution. I doubled this recipe to make enough for 34 students working in pairs.

• 1 cup distilled water

• 2 tbsp Karo light corn syrup

• 4 tbsp Dawn dishwashing liquid

I put the bubble solution in small plastic cups. Paper cups do not work! I give students embroidery threads to use as "string" to measure diameter and circumference. Of course they then have to measure the string against a ruler to get a reading in centimeters.

They work in pairs — one person blows a bubble and measures, the other person records; they wipe off desk, string, and ruler after each bubble. Switch roles. I ask for at least five different-sized bubbles.

Not wanting to waste the leftover bubble solution, I let the kids go outside to blow bubbles in the Friday afternoon sun. One kid said, "Today is such a good day." Other kids quickly chimed in to agree.

I really think they will remember that the circumference is about three times the diameter.

A Lesson Salvaged

The intended activity from MAP did not go well last week.

I gave these instructions:

1. Pair up. One person is the Describer, the other the Drawer.

2. The Describer is going to look at a Roman mosaic and describe it to the Drawer to draw it.

3. Both people may talk to each other, but no hands or any other bodily gestures.

4. The Describer may not look at the Drawer's paper as he/she works on the drawing.

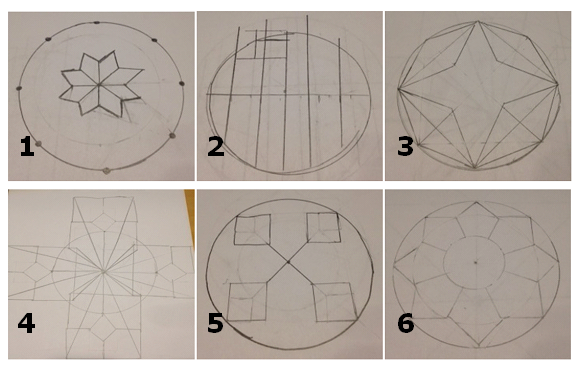
I gave each Drawer a blank sheet of paper. I gave each student a ruler and a compass. And I gave each Describer a picture of this.

I also told the Describers to get their Drawers to get the size just right — thus the ruler. I encouraged the Describers to use words like rotate, reflect, symmetry. After a while, I walked around looking at the papers and thought, Holy Cow, if-only-you-could-see-what-your-drawer-is-drawing.

I called for the Drawers' papers after about 30 minutes. The results:

What the...? Oh, let's not forget No. 7. Sketches 4 and 7 took up most of the 21.5 cm x 28 cm paper; the actual mosaic was 8 centimeters in diameter.

Then, I thought, Let me try being the Describer!

The results

Sketch D was very close, considering we were all hurrying through as the period was ending. Still, this was not my assignment and not a fair comparison when I had a lot more time to look at the shape. I took the stack home and let it mingle with the other piles of papers on my desk.

Late last night I looked again at the sketches on my desk and thought, I should try to construct this shape in Geometer's Sketchpad (GSP).

It was not an easy task!! I had to really think about each step and kept wondering during my construction if there was a better or more efficient way to do this. I felt great when I was done because it was challenging. No reason to keep this experience to myself, so I asked my geometry kids this morning to construct the Roman mosaic in GSP!

I reminded them that their constructions must pass the "drag test," meaning their Roman mosaic must not collapse when any vertex got dragged about.

Five minutes into the construction, Bobby said, "This makes me crazy!" Yes!

Some works in progress:

Karie was one of the first ones to finish; she talked about her construction:

Alex talked about his construction. You could hear the dismissal bell while he was talking, but no one got up to leave or put away the laptops. I had to tell them!

It was cool that the five students who had finished all had different ways of constructing the mosaic. Theirs were much more elegant than mine. More importantly, my construction did NOT even pass the drag test when I tried it this morning, but I intentionally forgot to tell them this.

A lesson salvaged by GSP. A teacher schooled by her 8th graders.