My Other Math Sites
Lessons From the Classroom
Math Worksheets
I often create worksheets for my students, even though every district-adopted math curriculum we've had has worksheets for students. I do this for two reasons:
I sometimes want to teach differently than what the curriculum writing team was thinking.
There's a particular structure/scaffold that reflects how I see the content can unfold for learners.
Here's a sequence of practice questions for my 8th graders on rigid transformations.
Everything about this is intentional.
Item #1 is a completed sample of what's to come. This is a practice worksheet, not a problem-solving task, so I will be clear about what is expected.
I remove certain parts in item #2, while keeping it similar to item #1.
Item #3 comes before item #4 because I think it's easier to follow the stated transformations than to say what they are.
Item #6 asks for more flexibility but with an ending constraint.
Item #7 opens up the problem and allows for peer exchange.
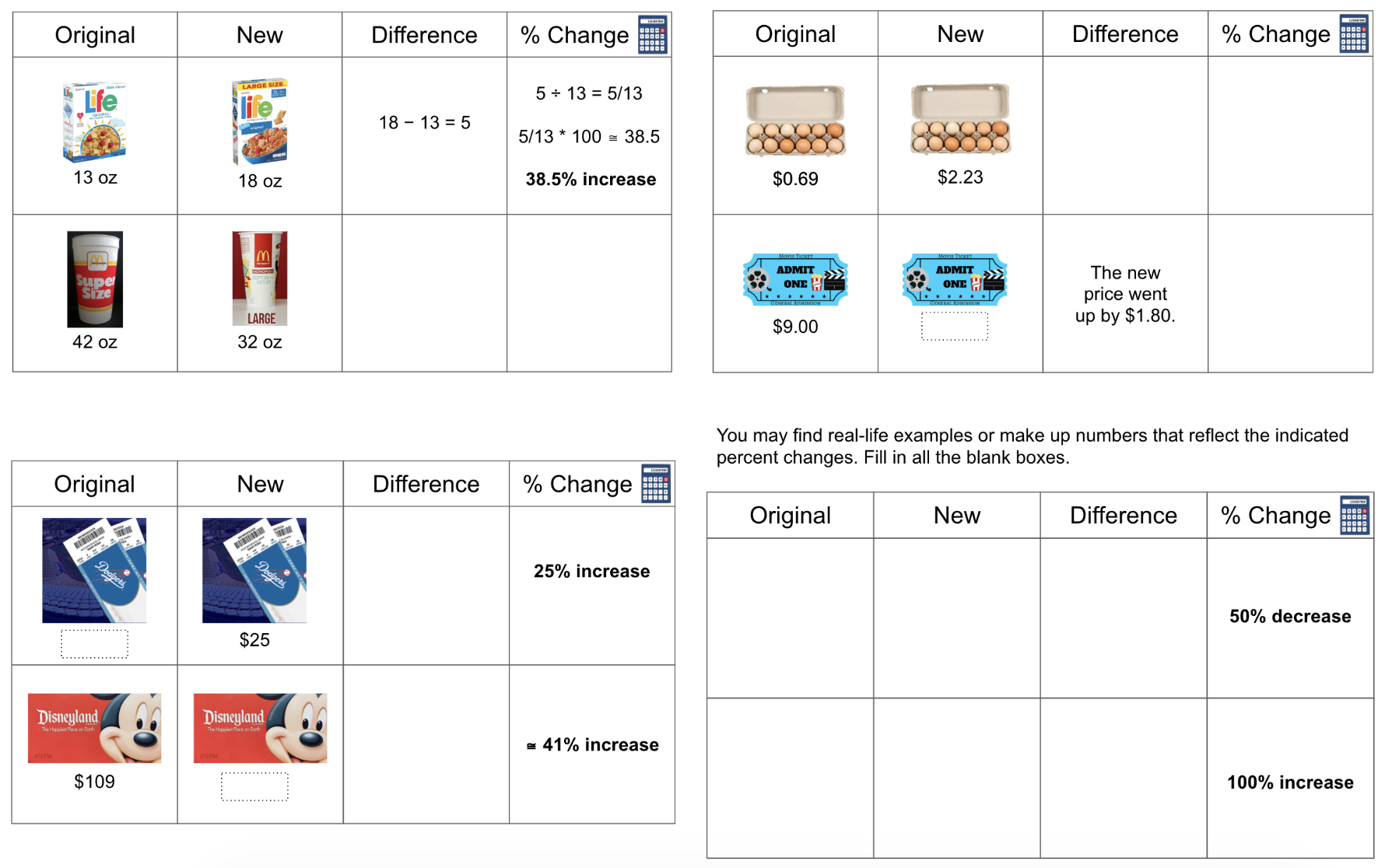
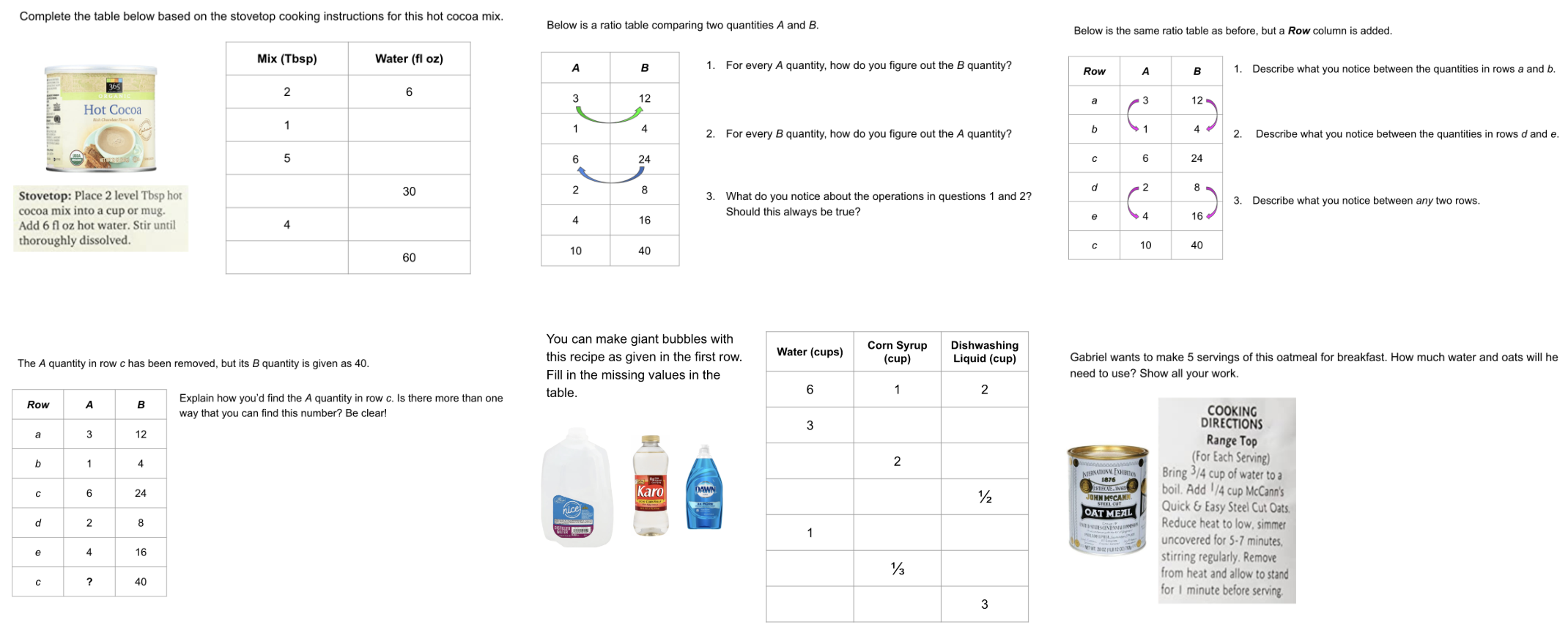
It's esthetically easier for me to create the questions on Google Slides. I then do screenshots to toss them onto a Google Doc. Here's a screenshot of questions for 7th graders on percent change. Here's a screenshot of questions for 6th graders on ratios and rates. If you'd like copies of these:
Yes, each of these takes one unit of shit-ton of time, especially when I have to look up real products with real numbers. But it's an OCD thing too, as in If-I-can-make-it-better-I-will. Stay safe, everyone.
Rigid Transformations
My 8th graders are learning about rigid transformations. I want to add a bit more complexity to what our book is asking the kids to do. For example, the book is having them reflect a shape mainly across the x-axis or y-axis, or on a rare occasion, reflect it across "the horizontal line that goes through y = 3." Well, right before this chapter, we've been working with writing and graphing linear equations, so I want kids to reflect a shape across any line, including one that may cut through the shape itself.
The book surprisingly has very few examples and exercises with rotations. And from what I can find, all these rotations happen about the origin or about a point coinciding with one of the vertices of the shape. Again, I want kids to be able to rotate a shape about any point, including one that's inside the shape. (I used a playing card — number 7 works well because it's asymmetrical — poked my pencil through it as the center of rotation, and turned the card. I think this helps them see what I keep referring to as the pivot or anchor point.)
Then I give each student this task:
Draw a shape that has between 5 to 8 sides with no curved edges.
Transform your shape through at least 3 rigid transformations of rotation, translation, and reflection — in any order.
On grid paper, give your teacher your complete work on this, including the written directions for the transformations.
On grid paper, give your teacher only the original shape and the written instructions. Your teacher will give this paper to a random classmate to follow your written directions to arrive at the intended location of the final image.
For students who want more challenge, they may ask for a copy that has just the original shape and its final image without the written directions. The task will then be to figure the appropriate transformations that connect the two images.
I really believe that it's good practice to always give kids more than what we believe they can handle. Let kids tell us when it's too much for them — and we find out soon enough. An ounce of struggle on something hard is worth a pound of completion on something easy.