My Other Math Sites
Lessons From the Classroom
Fractions Operations Using Rectangles
A few days ago, Mary had replied to Nat’s tweet.
@fawnpnguyen is the queen of this. Pretty sure she has a blog post on it.
— Mary Bourassa (@MaryBourassa) May 14, 2021
God, I love Mary. She sent me a decadent chocolate bar from 2,800 miles away. She remembers my birthday when 2/3 of my children did not.
I am queen only in my own head, and no, I did not have a blog post on adding fractions. I thought surely there must be a wide assortment of videos on adding fractions using rectangles. But the very first two that I’d clicked on - this and this - really astonished me. They both used grid papers without using the grids. Like, what the heck.
Say we want to add 2/3 and 4/5, same two fractions that popped in my head when I replied to Mary.
Draw two same-size rectangles using the denominators as dimensions.
Students will ask, “Why 3 by 5?” If they don’t, you ask why. And you answer them by asking them to shade in 2/3 for one rectangle and 4/5 for the other. Give them a few seconds to do this and they’ll understand why the 3 by 5 rectangles work pretty well here.
We’re adding the fractions, so let’s combine them.
Similarly with subtraction of fractions.
For multiplication, the word “of” is useful. Of course, the commutative property of multiplication applies too.
To take 2/3 of 4/5, we’d look along the height in this rectangle as we can see the thirds and just grab two of the sections.
Likewise, taking 4/5 of 2/3 is to look along the width of 5 and grab 4 sections of it.
I’ve written about division of fractions previously:
Green Olives
My 7th graders are working on "percentages of" problems currently, and late last night, I saw this problem on one of Don Steward's handouts.
There are 75 olives, 40% of which are green. I eat some of the green olives until 10% of the olives that remain are green. How many green olives did I eat?
How would you solve this? I solved it using algebra. Then, immediately, I thought, Fawnzie, since when do you use algebra to solve stuff like this. C'mon, do your rectangles.
I think of 40% as 2 of 5 boxes.
So, 75 olives must split into 5 groups of 15, so there are 30 green olives.
Then, I ate some olives to end up with only 10% of the remaining olives are green.
Well, since I didn't eat any of the 45 black olives, so these 45 must make up 90% of the olives remaining [in the 9 boxes], so 45 must split into 9 groups of 5.
Oh, look! I began with 30 green olives, I now only have 5 green ones left, so I must have eaten 25 of them.Okay, your turn.
There are 80 olives, 75% of which are green. I eat some of the green olives until 20% of the remaining olives are green. How many green olives did I eat?
I’d rather use the drawings than show them my work below.
Euclid's Algorithm
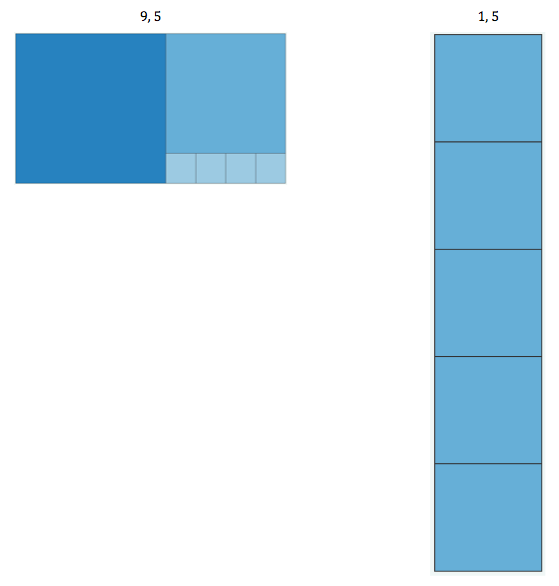
I show my 6th graders this image, pointing out that this picture represents the two numbers 1 and 1 that I'd entered at the top.
I then ask them to give me two new numbers — any two positive integers [that are 10 or less, for now] — and the computer will draw a new picture. As each set of new numbers is entered and the corresponding picture is generated on the screen, I ask students to jot down their "I notice, I wonder" in Google Form and to draw a rough sketch of it in their journal. After a few sets of numbers, I ask students to imagine and/or draw a rough sketch of what they think the picture will look like before I hit the update button.
These are the pairs of numbers they'd asked for and their corresponding pictures, listed in the order that was asked.
I love that the kids are asking for...
6, 6 after the initial 1, 1
3, 8 after 3, 1
8, 3 after 3, 8
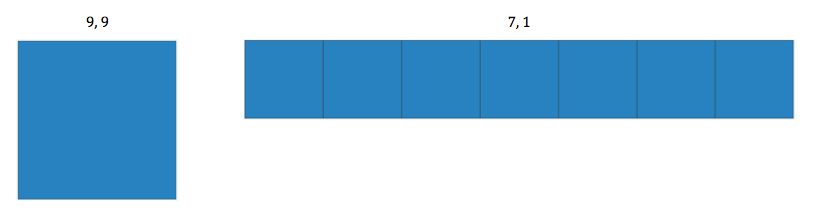
But, when sets 9, 9, and 7, 1 are asked at the end there, I say to the class, “Hey, what if figuring out this puzzle — which is how the computer draws the picture given two numbers — gets you a million dollars. And you get to ask for sample sketches like you've been asking, except that each sample costs you some money! So, make each request worth it. Let it prove or disprove your conjecture. Ask carefully."
I love the OHHHs and AHHHs after each picture is revealed. But no one is claiming that he/she had drawn the same diagram. I pause longer for them to write down their noticing and wondering.
I now say, "You may only ask for four more sets of numbers. Remember, make a request that would test your conjecture."
I ask a normally quiet student. She says, "10, 3."
Another student wants to know what "100, 5" looks like.
"What about 8, 5?" I reply, "Sure, but draw it in your journal first." They are fully engaged. Then I say, "Now, share your drawing with a neighbor."
I ask, "Did anyone sketch the same thing as their neighbor?" They're shaking their heads, and I say, "That's pretty crazy! Do you think yours is more 'correct' than your neighbor's?"
I reveal 8, 5.
The last request is 23, 75.
What some of them have written [with minor edits from me]:
When we did the same two numbers the shape didn't change but when we did different numbers it changed. Why does it divide into little parts within a square when we put 3,8? When we did 8,3 the number switched around. I wonder if the two numbers are dividing to make the shape. How can you figure out the number when it can't divide easily. My drawing for 8,5 was one whole and 5 little squares. The 23,75 was a little confusing to me.
They're different, they are the length and width, and when the two numbers are the same it's just one cube. I notice that if it can be simplified, it is. Example: 6,2 = 3,1. I don't understand 8,3, 5,9, 23,75 or 8,5. But I did notice that the smaller the parts of the shape are, the lighter shade of blue they are.
I observe that when the same numbers are entered it equals to a blue square. If the first number is bigger than 2 then it will add one more square. I wonder if you double the number for each number will it be the same shape. I wonder why for 3,8 it has one square with three parts. I observed that if you divided the first number by the second it will equal to the number of squares. For 8,5 I didn't get the right sketch. The sketch was one square with half of a square cut in half, then in one half is has a strip that is cut in half. I wonder why it has half of a square. I think that my answer for how it figures it out is right, but I don't know how it comes up with that picture for 8,5.
When you do 1 and 1 it doesn't change because we tried 6 and 6 it didn't change and if we put 3 and 1 it did change. I saw that when we did any number like 3 and 1 is 3 ones. So I think that all you have to do is divide something by something = the first number that you put in but if you can't divide by 2 then I'm wrong. I'm not sure that I got this right but this is what I think.
For the first one 1 and 1 I thought it would be a small one by one cube. What threw my off was the 6 by 6 because the size did not change. For the 8 and 5 I drew a big block and and 5 little ones, but my image was wrong. I also wondered if the first number was the amount of shapes that would appear, but I was wrong again. I don't understand yet. I tried looking for a pattern, but couldn't find one.
When I tried 8,5, my answer was almost right. I had the one big square right, the half square right, but then I got the little squares wrong. I think that the way the computer does it is dividing the first number by the second number. I am confident that if you put the numbers 10 and 5 in, it will show 2 squares. When using the diagram, the second number will represent the vertical side.
What I've been noticing was that if you put the bigger # in the front and the small # last then it would be like a rectangle. I've also been noticing that if you put the same #'s it would like keep on drawing a square. So someone said what could (8,5) look like and Ms.Nguyen showed us the drawing and the I notice that nobody got it right. I was expecting something like smaller because the #'s were small they weren't as big, but at least I tried to get it correct but I drew something a little bit smaller than that. I also wondered why when we put the same #'s together why do they all become a square that's what I wonder.
For 5, 12 I notice that it is two big squares, two smaller squares, and two tiny squares, I thought it was going to show 1 big block and another big block but that one would be cut off at the bottom or not a whole block. I also notice that the pattern is the first number multiplied by what equals the second number and the number that is missing is the amount of blocks that is created. I thought I knew it but I don't really get the ones with a bigger number first and the smaller one last. I thought I knew what 9, 23 was going to be but it the result was surprising. It didn't look at all how I thought it was going to. The website is pretty cool, but one thing I didn't understand was the placement of the small blocks and what they stand for. Like some were really tiny and some were small but I don't know what they stand for. But I bet if someone explains it to me I probably will understand perfectly and feel dumb.
The only thing that I am sure that I know is that when the first number is larger than the second, the shape is wide and when the second number is larger, the shape is tall. Other than that I am very confused.
Then, together as a whole class, they agree on the following;
When both numbers are the same, then the picture is one square.
The computer simplifies the two numbers, such that a picture for 6, 3 is the same for 2, 1.
When the second number is a 1, then the picture shows the first number of squares. For example, 7 and 1 would form a picture of 7 squares, and 100 and 1 would form 100 squares.
The first number is the horizontal dimension, while the second is the vertical.
They are all squares.
The dismissal bell is about to ring, and I want to teach forever.
Tomorrow, we'll spend some time with one set of numbers, like 10, 3 or 8, 5. We'll dissect the diagram. Play around with a few more. Practice sketching a few. We'll write out the equations that go with each diagram. I'll guide them into noticing the size of the smallest square in relation to the two numbers.
I found this investigation at underground mathematics. The site describes itself as having "rich resources for teaching A level mathematics." From what I understand, "A level" means advanced level mathematics consisting of core modules ranging from quadratic, logarithms, geometric/arithmetic series, differentiation/integration, etc.
Perfect for my 6th graders who continue to torment me with their arithmetic atrocities, such as, 3² = 6 and 5 ÷ 10 = 2.
While the original task is scripted for older and more advanced students, I found in it what I needed to make it rich and appropriately complex for my 6th graders.
Hail, Euclid's algorithm!
Dividing Fractions
My 6th graders have been working with dividing fractions for the last two weeks. We explore these four ways, in this order:
Number line
Rectangles — I wrote about this here.
Dividing by one
Common denominator
It's completely intentional that we work with the number line and rectangles first. I want my kids to see the answer and that it should match their intuition and understanding.
Multiplication: Finding the Greatest Product
From a set of 1 through 9 playing cards, I draw five cards and get cards showing 8, 4, 2, 7, and 5. I ask my 6th graders to make a 3-digit number and a 2-digit number that would yield the greatest product. I add, "But do not complete the multiplication — meaning do not figure out the answer. I just want you to think about place value and multiplication."
I ask for volunteers who feel confident about their two numbers to share. This question brings out more than a few confident thinkers — each was so confident that he/she had the greatest product. (I'm noting here that I wasn't entirely sure what what the largest product would be. After this lesson, I asked some math teachers this question, and I appreciate the three teachers who shared. None of them gave the correct answer.)
I say, "Well, this is quite lovely, but y'all can't be right." I ask everyone to look at the seven "confident" submissions and see if they could reason that one yields a greater product than another, then perhaps we might narrow this list down a bit.
Someone sees "easily" that #7 is greater than #6. The class agrees.
Someone says #7 is greater than #1 because of "doubling." She says, "I know this from our math talk. Doubling and halving. Look at #1. If I take half of 875, I get about 430. If I double 42, I get 84. Both of these numbers [430 and 84] are smaller than what are in #7. So I'm confident #7 is greater than #1."
Someone else says #5 is greater than #4 because of rounding, "Eight hundred something times 70 is greater than eight hundred something times 50. The effect of multiplying by 800 is much more."
Someone says, "Number 2 is also greater than #1 because of place value. I mean the top numbers are almost the same, but #2 has twelve more groups of 872."
But the only one that the class unanimously agrees on to eliminate is #6. Then I ask them to take 30 seconds to quietly examine the remaining six and put a star next to the one that they believe yield the greatest product. These are their votes.
I tell them that clearly this is a tough thing to think about because we've had a lot of discussion yet many possibilities still remain. And that's okay -- that's why we're doing this. We've been doing enough multiplication of 2-digit by 2-digit during math talks that it's time we tackle something more challenging. So #3 gets the most votes.
I then punch the numbers into the calculator, and the kids are very excited to see what comes up after each time that I hit the ENTER key. Cheers and groans can be heard from around the room. Turns out #3 does has the greatest product (63,150) out of the ones shown.
Ah, but then someone suggests 752 times 84. I punch it into the calculator and everyone gasps. It has a product of 63,168.
Their little heads are exploding.
I give them a new set of five for homework: 2, 3, 5, 6, and 9. They are to go home and figure out the largest product from 3-digit by 2-digit multiplication. They come back with 652 times 93.
The next day, we try another set: 3, 4, 5, 8, and 9. We get the greatest product by doing 853 times 94. There is a lot — as much if not more than the day before — of sharing and arguing and reasoning about multiplication and place value.
Many of them see a pattern in the arrangement of the digits and are eager to share. They've agreed on this placement.
Then we talk about making sure we know we've looked at all the possible configurations. They agree that the greatest digit has to either be in the hundreds place of the 3-digit number or in the tens place of the 2-digit number. We try a simple set of numbers 1 through 5, and we agree that there are just 9 possible candidates that we need to test. The same placement holds.
Then we draw generic rectangles to remind us that we've just been looking for two dimensions that would give us the largest area.
I remember saying to the class, more than once, that this is tough to think about. To which Harley, sitting in the front row, says, "But it's like we're playing a game. It's fun."
Dissecting Polygons
I appreciate any math lesson where I give the students minimal instruction, yet the lesson is rich in content and it gets kids to do math. (I'm learning to do more and more of not doing much.)
Each student got two pieces of grid paper.
Part 1
In portrait orientation, fold paper in half vertically and approximately into thirds horizontally. Unfold paper to see the six sections created by the folds. Repeat with the other paper. Number the two papers from 1 to 6, like this.
Then I gave each student a ruler and these instructions:
In section 1 of your paper, draw a parallelogram. Find a way to cut your parallelogram into pieces that you can rearrange to form a rectangle. (Here I clarified what I meant: all the cut pieces from the original figure must be put together again to form the requested figure without gaps or overlaps — like a jigsaw puzzle.)
I gave students more graph paper and encouraged them to redraw the parallelogram so they could actually make the cut(s) using scissors. But for this first question, the kids were able to just make a "visual" cut — showing it as a dashed segment — and the requested figure was drawn in the section to the right of the original figure, something like this. (Two students' original parallelograms were rectangles, and that was perfectly okay.)
When everyone understood the directions, I gave out the next five challenges — all as oral instructions.
In section 2: Start with a right triangle. Cut it into pieces that will form a rectangle.
In section 3: Start with a scalene, non-right triangle. Cut it into pieces that will form a parallelogram.
In section 4: Start with a scalene, non-right triangle. Cut it into pieces that will form a rectangle.
In section 5: Start with a trapezoid. Cut it into pieces that will form a rectangle.
And in section 6: Start with a trapezoid. Cut it into pieces that will form a triangle. (See if you can do this with a single cut.)
The kids were really engrossed in this activity!
They were doing a lot of drawing and re-drawing; they were cutting each polygon into pieces and manipulating them.
What they said during the activity:
What the... Oh, I gotcha.
No cheating, J. (to which J. responded with "I am ahead of you, dude!")
I have number six done!
Yeah, but did you do it with one cut?
Z. is on number six because he skipped 4 and 5.
I'm still working on number three...Why can't I draw a scalene triangle?! UGH!!
Can I flip a piece? (I didn't think of this, so it certainly wasn't part of my instruction. We discussed and agreed that you may NOT flip a piece over. Kids started labeling their pieces or coloring one side so they wouldn't accidentally flip them.)
I later asked them to add color to the different edges of the polygons/cut pieces with different colors to make it easier for someone to follow how the pieces had translated after the cut.
No one had finished all 6 tasks; most were working on task 4, so I asked them to spend about 30 minutes more on it for homework.
Tomorrow I'll check their progress on Part 1. I'll ask kids to come up and share their ways of dissecting the polygons. Then we'll move on to Part 2. But I'll be sure to collect their work on Part 1 first because I don't want them to look back at Part 1 to do Part 2 — I'm just mean that way.
Part 2
Sort of like the reverse of Part 1. In Part 1, students were asked to dissect various shapes and rearrange their pieces to form mostly rectangles. While in Part 2, students will begin with rectangles and dissect each one to form these shapes: 1) an isosceles triangle, 2) a right triangle, 3) a scalene triangle, 4) a non-rectangular parallelogram and 5) a trapezoid.
I'm so excited for tomorrow because this went so well today! I love math and I love my students!!