My Other Math Sites
Lessons From the Classroom
Math Worksheets
I often create worksheets for my students, even though every district-adopted math curriculum we've had has worksheets for students. I do this for two reasons:
I sometimes want to teach differently than what the curriculum writing team was thinking.
There's a particular structure/scaffold that reflects how I see the content can unfold for learners.
Here's a sequence of practice questions for my 8th graders on rigid transformations.
Everything about this is intentional.
Item #1 is a completed sample of what's to come. This is a practice worksheet, not a problem-solving task, so I will be clear about what is expected.
I remove certain parts in item #2, while keeping it similar to item #1.
Item #3 comes before item #4 because I think it's easier to follow the stated transformations than to say what they are.
Item #6 asks for more flexibility but with an ending constraint.
Item #7 opens up the problem and allows for peer exchange.
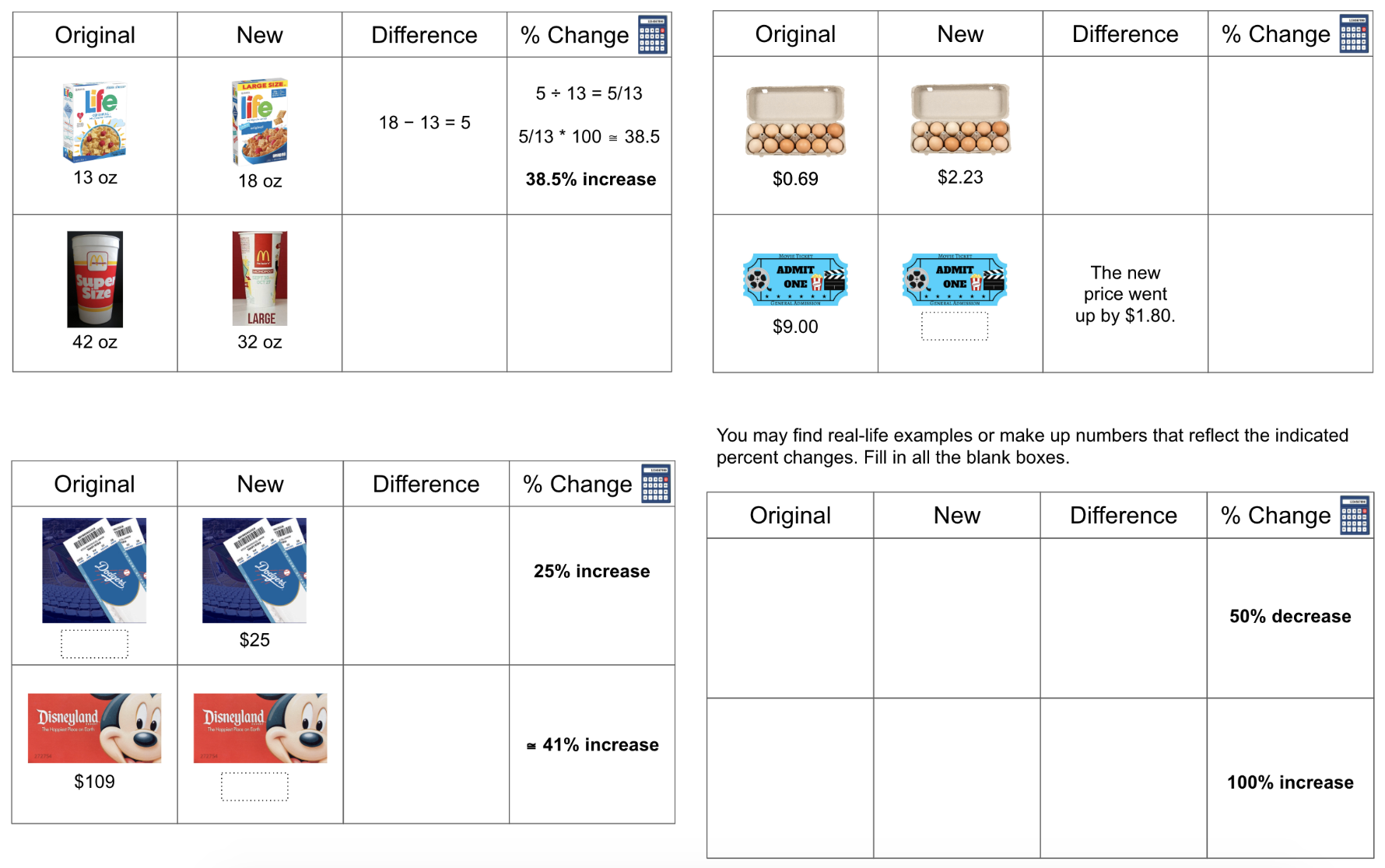
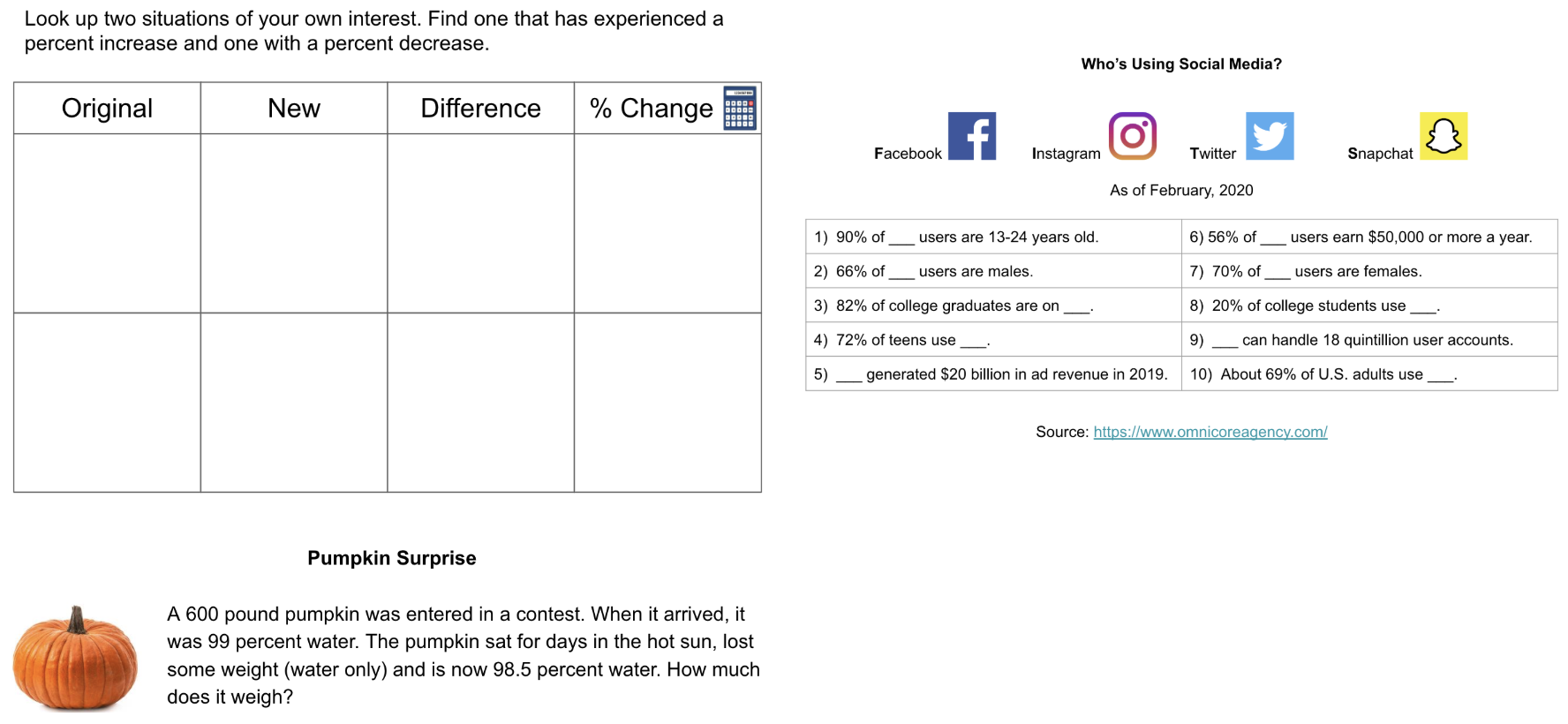
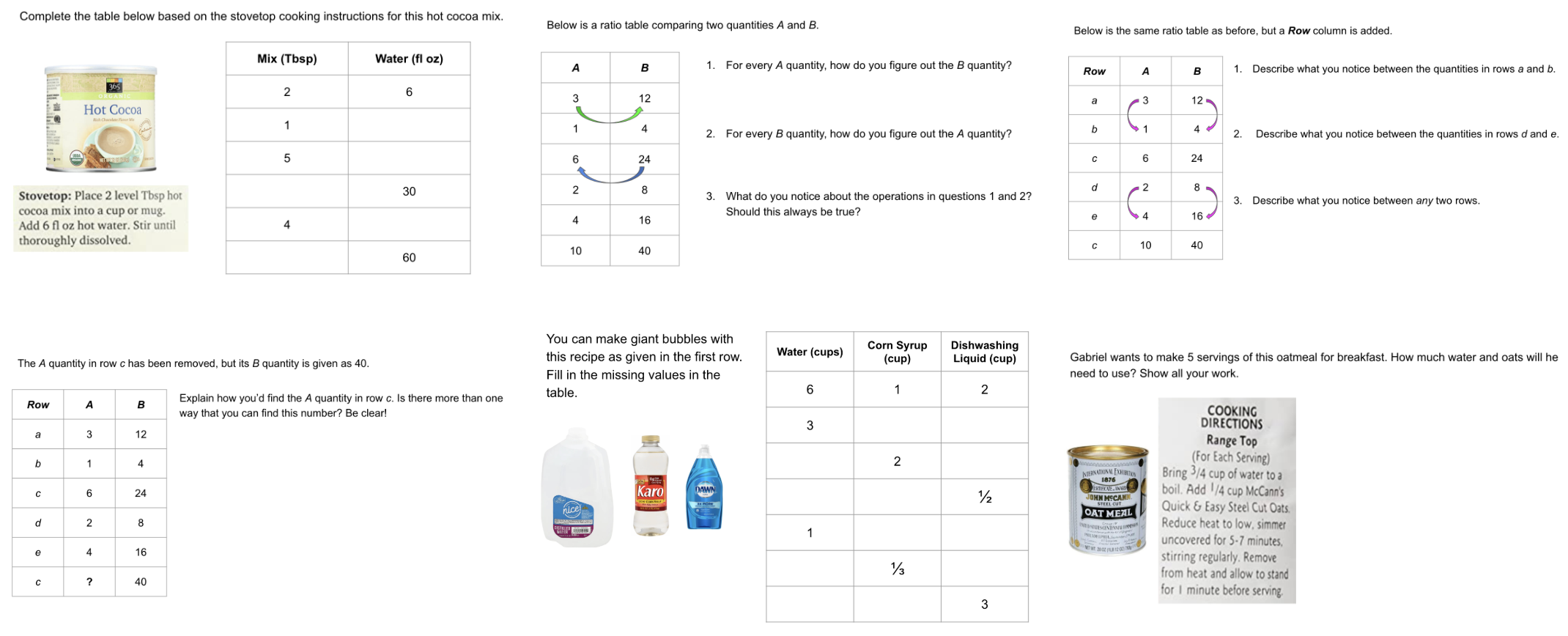
It's esthetically easier for me to create the questions on Google Slides. I then do screenshots to toss them onto a Google Doc. Here's a screenshot of questions for 7th graders on percent change. Here's a screenshot of questions for 6th graders on ratios and rates. If you'd like copies of these:
Yes, each of these takes one unit of shit-ton of time, especially when I have to look up real products with real numbers. But it's an OCD thing too, as in If-I-can-make-it-better-I-will. Stay safe, everyone.
Reversing the Question
Don Steward posted this on Sunday. Like Don, I really like this task and also think it has a certain Malcolm Swan je ne sais quoi about it.
I showed only the top part to my 6th graders, and I gave them 2 minutes to write down what they noticed.
In addition to noticing the given information, the students also mentioned:
It takes a lot of grams to make a sponge cake.
A kilogram must have a lot of grams in it.
The unit of measurement is changed in the cake and in the big bag.
This problem doesn't have a question.
The sponge cake has no price.
There is frosting on the cake.
You need to change the measurements first (kg - g)
The cake weighs more.
The cake is really small and the flour is really big.
Not much information and there's no question.
There is no question.
The weight of the bag is in kg but the flour it takes for the cake is in g.
You have to convert 24 kg to grams.
It uses only very little of the flour.
I gave them another 2 minutes to write down what they wondered.
How much the sponge cake costs.
How many sponge cakes can you make.
How big is the sponge cake.
How to convert from kg to g.
If the sponge cake is good.
24 kg is <, =, or > 150 g.
What we are going to have to solve.
Is the question going to be about if there's enough flour or is it going to make us change it from kg to g.
How much 24 kilograms is in pounds.
How many grams are in a kilogram?
How many krumkakes can you make with the bag of flour.
How long will it take for the cake to be ready.
What a sponge cake is and what the recipe is for the cake.
How much flour is left.
What flavor is the cake. (Sorry. I'm hungry!)
What you're wondering that I'm wondering about.
What the question is, and if there are more ingredients.
If we will have to find the price for the sponge cake, or maybe we have to find out how much half as much flour is worth.
Then we moved on to next part of providing questions that would go with the calculations. This was so very tough for my kids. While 21 of 31 kids could come up with the correct question for part (a), they were lost with what to write for the other three parts.
Because we didn't care what the numerical answers were, the kids didn't do any calculations, instead they were supposed to focus on the operation(s) in each problem and decide on the question that would prompt a specific operation.
The most common question for part (b) was, "How much does 1 kg of flour cost?" (I'd swapped out £ for $.)
Then my next step would be for them to go ahead and use a calculator to get the numerical answers. They will see that for part (b), 24 divided by 21.50 equals approximately 1.12. And if 1.12 were the cost for 1 kg of flour, then 24 kg of flour should cost more than $24. But, wait. We already know that the bag of flour costs $21.50. Hopefully they'll arrive at this contradiction on their own, and re-think their question.
We'll then attach the units to the numbers accordingly and let the conversations continue. When kids tell me that they will calculate two numbers using operation w, I always follow up with, What does your answer mean? What unit or units does it carry?
Too often kids have trouble with word problems. Too often they don't know what to do with two numbers let alone a bunch of numbers. They guess at division when one number is big and one is small. They add when they see two fractions. They multiply because that was how they solved the last word problem.
I will also do this with my 8th graders because I suspect they will have trouble too. And this is exactly the kind of trouble we need to get into. Now rather than later. This task gets them thinking about ratios — which is like the most important math thing in all of the math things.
Steward is exactly right about this task. And I'm thankful he shared.
It was used as a fine example of how reversing the question can often lead to a more challenging task.