My Other Math Sites
Lessons From the Classroom
A Routine for Between 2 Numbers
I hadn’t realized the last few entries of between2numbers.com were left blank. They are done now. Thought I’d share a more revised warmup routine of how I’ve used the contents.
I’ll use entry #1 as an example.
I project the two images only and set the timer for 30 seconds for quiet notice-and-wonder. No writing necessary during this time.
I then say, “Before I show you the speed of each of these, I’d like you to discuss with a neighbor what the numbers might be, let’s think miles per hour.” I ask them to write down their estimates [in a journal]. Set the timer for another minute.
I call randomly on two students to tell the class what their guesses are for the snail. Call on two more students for their guesses for the jet. I record these on the board.
Now I reveal the snail’s rate and ask, “Who has the closest guess to this?” Record their answers. This is a good opportunity for students to check their decimal comparison.
Now I reveal the jet’s rate and ask for the same.
I entertain any other related information at this point. I might ask them if they knew what the average speed of a passenger airplane was. Then, I reveal the question.
Okay, this step is important. It saves time writing and fussing over actual quantities, and I find that it helps students focus on the mathematical operation rather than feel anxious about the numbers. I say, “We’re going to let the snail’s rate be A, the jet’s rate be B, and the distance 2,800 miles be C…”
“... Discuss with your neighbor what calculation(s) you would do to find out how much time it takes each object to travel across the US. Just use the letters now. For example, if you wanted to add the two rates, you’d just write A + B.” Set the timer for one minute.
Randomly call on one group to share. Record on the board what they share and ask, “Who has a different solution?” Write down what they say. Continue asking until I have recorded all the different solutions. (Normally, there are usually just 2 or 3 different ones.)
I now take out a calculator and get an answer for each of the solutions shared. I go back to the owners of each solution and ask, “What unit should your answer have?” (If the units were not mentioned earlier.) We discuss the reasonableness of the correct answer.
I’m proud of this site because the routine affords several of these:
interesting facts
estimating
talking and listening
proportional reasoning
unit rates
dimensional analysis
Here is the key. Please share this resource widely, and if you use it, please let me know how it goes.
Greenies
Our black lab Mandy is 3.5 years old, weighs a ton, and her breath used to smell like death. Until we started giving her one Greenies a day. My husband orders them from Amazon, he also gets them for our neighbor's small dog Bailey.
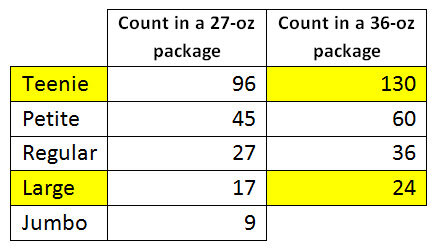
Although both boxes weigh the same 36 ounces, Bailey gets 130 treats in the Teenie size and Mandy gets only 24 in the Large size. This caught my attention which led to this task with my 8th graders who happen to be working with similar shapes. (Like I had planned this all along.)
Greenies are sold in various size packages. I'm interested in the 27-oz and 36-oz.
To launch the task, I hold up the 2 treats: 1 Large and 1 Teenie. I tell them that there are 24 Large ones in a 36-oz package, and I want them I guess how many Teenie ones are in a 36-oz package.
Then I give the students these:
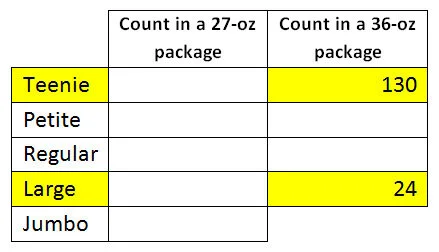
The photo of the 2 packages (so they know only the highlighted information in the table above).
Each group of 3 students get two real treats: 1 Large and 1 Teenie.
In return, the students need to give me these:
A 2-dimensional outline (with dimensions labeled) of what a Petite, a Regular, and a Jumbo may look like. For example, these are the actual outlines of the Large and Teenie. They may write down the thickness also.
A completed table with the missing counts filled in.
Highlights of this task:
Kids use some known information to construct new information. They use modeling to figure out what the other sizes may look like and how many of them would fit in a 27-oz or 36-oz package.
It's kinda messy and weird. While the kids can measure whatever lengths of a treat, how do these numbers translate into the mass of each treat?
It's good to work with solid objects instead of just flat polygons when learning similar shapes.
The reveal (Act 3) of something like this is always a lot of fun. Not only the reveal in the count per package, but also how close their outline sketches are to the actual treats when I bring in the Petite, Regular, and Jumbo.
How much does a 36-oz package cost?
Is the Jumbo a shot in the dark? Would kids think to ask me for the size of the dogs? How does this help, if at all?
Prices, Proportions, Percents
I was in Garden Grove with my son on Sunday, and he insisted that I try this smoothie place called Tastea. With Jamba Juice and Blenders and all the other juice bars around town, I was skeptical that this joint's concoctions would be anything different. He ordered a taro milk tea and I got a Thai tea, both with boba. Just one sip and I said to him, "Let's order another round! It's a long drive home!" Soooo delicious.
While there I saw a math lesson brewing, so I picked up their menu with prices. This is the lesson with my two classes of 6th graders.
Me: (I tell them about Tastea and how I wish it were closer.) Okay, let's start with something you might be more familiar with, Starbucks. I love that now I live within walking distance from one! Do you know the different sizes that they have there?
Class: (When I refer to "class," I don't mean the whole class, of course, but somebody in the class joins in on the conversation.) Tall, grande, venti.
M: Do you know exactly how much liquid each size holds? (They make various guesses. I bring out the 3 sizes that I got from Starbucks so they have a visual.) I normally order a tall mocha frappuccino, let's say the price is $3.50. Do you think the venti, which is twice the volume of the tall, would cost twice as much, or $7.00?
C: No.
M: Why not?
C: You normally get a better deal with a bigger size.
M: What do you mean by a "better deal"?
C: (All their answers show me that they understand the idea of more bang for your buck. Then finally someone says...) Lowest unit price!
M: Right! That's why so many families go to Costco. Buying in bulk normally saves us money because the item has the best unit price. Well, we're talking about Starbucks now, so buying more is a better deal, but drinking more is not so good for our body. Let's fill in this sheet. (I pass out this handout. And here’s the key.) How do we calculate unit price? What place value should we round it to? How do you write thirty-one-cents-per-ounce?
M: Tastea has three sizes: mini, gigantic, and even more. Their teas can also be purchased by the "partea jug," which holds a gallon. I've given you the prices of the 10-ounce minis for the three different types of drinks, your job is to figure out the prices of the other sizes. You'll work in small groups to figure out these out. So, do you think the gigantic will cost twice as much as the mini because it holds twice as much?
C: No. It'll cost less.
M: How much less? Well, that's your group's job to come up with the best estimate. We have Starbucks' prices for their three sizes, you could look at how they price their drinks. But here's the sweet deal for you. You and your group mates do the math that you need to, then write down your first estimation right here in this column. Bring your paper up to me (only the "captain's" paper), give me a few seconds to figure out the percentage that your estimation is off by, and I'll write it in this column and give you back your paper. What percent do you want to see, large or small? What if your estimation were the actual price — what percent would I write there?
I tell them that they could figure out the actual price of the drink if they knew how I calculated the percentage of error. So, work work work. Think think think. What makes sense? Oh, I remind them that the percentage does not indicate if their estimation is too high or too low. So, again, what makes sense?
We also note that prices generally end in a 0, 5, or 9. So, even if the calculation tells them the price should be $4.23, they might want to change that to $4.25 or $4.20.
When they bring up their paper again with the second estimation, all I do is write their estimation again in pen and circle it — this is so they can't change their answer and I know that I've seen it. I do NOT fill in the "Actual Price" column at this time because the groups are working at different rates, and in a crowded room, it's easy for kids to see each other's papers, even inadvertently, and the game of estimation is over if they saw the actual price beforehand.
They simply move on to the next size to make a first estimation again. We repeat the process.
When all groups are done with estimations for the first type of juice — smoothies — I tell them what the actual prices are.
Now, it's their turn to figure out the percentage of error. I give the groups about 10 minutes to do so without help from me. At the end of the 10 minutes, either there's at least one group that knows how to do so and can show it to the class, or no group knows how, then I'll walk them through the calculation by asking them questions to figure this out.
They continue in the same manner for the Slushy Freeze and Specialteas on page 2. This time hopefully they'll be able to work backward from the error percentage that I give them after their first estimation.
Reasons I'm proud of this lesson:
It's about proportions, but many priced items in real life are not directly proportional. The kids knew this coming in because they've been consumers.
We get to talk about business strategies that entice people to buy the larger sizes while still make a profit. (Starbucks calls it "tall" because it rhymes with "small," but clearly the word tall naturally elongates the imagination.)
Students get to make estimations throughout, but they know these aren't "wild-ass guesses." They start with the calculation of proportions and adjust the prices accordingly. They get to critique and argue with their group mates to come up with the best estimations.
I get kids to think about percentage in a context that they can wrap their heads around. And they want to know how because their second estimation could be dead on if they knew.
It's fun that the error percentage does not indicate if their estimation is too high or too low. A few groups do go farther in the wrong direction. Oh, well — good to learn that now.
It'd be fun for me to get Starbucks or Jamba Juice for the group with the lowest total in percentage errors.
Updated 04/05/14
I got some thoughtful reflections on this lesson, I'll just share two:
I learned how to work backwards with percentages and try to get the number spot on. I also learned how business would price things by dropping the price by the perfect amount. My number sense got a lot better from all the multiplying, dividing, and reasoning. It was very difficult, which I'm very happy about. The teamwork was probably the hardest part of the project. M and I are very competitive, and we got different answers a lot. I learned how to work together with others a lot better, and it doesn't move your team along to place blame and argue. I'm really grateful we did this project because it was very hard and worthwhile. It was a great use of three days!
I learned how to use different data to get answers. Also, we have to see a pattern. This Tastea assignment was really fun. I enjoyed it and look forward to another. Teamwork is really important even though people can't agree, you got to support it. If your group gets it wrong, but your answer was right, you can't blame someone or put them down because probably they will get some right for you. So always stay positive to your teammates and encourage them.
One Rod Tall
I’ve written before about reading books to my kids and following up with an activity. I read the poem One Inch Tall to my 6th graders as we’re studying ratios and proportions.
One Inch Tall
If you were only one inch tall, you’d ride a worm to school.
The teardrop of a crying ant would be your swimming pool.
A crumb of cake would be a feast
And last you seven days at least,
A flea would be a frightening beast
If you were one inch tall.
If you were only one inch tall, you’d walk beneath the door,
And it would take about a month to get down to the store.
A bit of fluff would be your bed,
You’d swing upon a spider’s thread,
And wear a thimble on your head
If you were one inch tall.
You’d surf across the kitchen sink upon a stick of gum.
You couldn’t hug your mama, you’d just have to hug her thumb.
You’d run from people’s feet in fright,
To move a pen would take all night,
(This poem took fourteen years to write—
‘Cause I’m just one inch tall).
Then I asked them to write their own poem in similar fashion (structure and style) using a unit length of their choice other than “inch.”
We agreed on the following guidelines:
minimum 18 lines, however many stanzas, no more than one page
rhyming is fun and recommended, but not necessary
typed up, size 12 font, no funky-impossible-to-read-annoying font
must be illustrated by hand, stick figures are okay as teacher can’t draw either
poem title and heading on paper
objects in the poem must be reasonably proportional
[Original post had more student samples, I’m just sharing one here.]
One Foot Tall
by Caden
If you were one foot tall, you would only be two pencils long
You would be barely taller than a math book
You could ride a big shade hat down a brook
You could sleep in a school backpack
You wouldn’t be able to reach the door handle
If you were one foot tall
If you were one foot tall, a roof would be a cliff
An iMac would be a flat screen TV
A sturdy folder would be a surfboard when riding in ferocious winds
A bathtub would be a hot tub to rest in
A Dalmatian dog would be a horse you could ride away on
If you were one foot tall
If you were one foot tall, a dog’s bed would be a perfect size
A desk chair would be a lounge chair to sit and rest in
The shrubs in the backyard would be a small jungle
A grape would be a plum
A kitchen sink would be a nice bathtub
If you were one foot tall
Speaking of reading and books and math, hot off the press is Nico Rowinsky‘s new ebook, Sally Strange. Nico clearly has a good pulse on middle school kids — he writes with heart and lightness and allows the mathematics to weave ever so gently through the pages. His Sally Strange is an all-too-familiar 7th grader in our classroom. Get it for yourself, for a friend, for a young friend, for your school library (when the hard copy comes out).
Visualizing Volume is Tricky!
This was one of those lessons that I think I gained a lot more than my 6th graders did. It was meant as a one-period activity, but I kept going off on different tangents and brought the students along for the ride.
Over a month ago Andrew Stadel tweeted me a picture that he took of a William Sonoma display of their cupcake mixes. I was at our local mall last Sunday and saw a similar display. We both thought about buying the mixes to make cupcakes for our kids, but it was $15 a can, and we'd need three, so the poor teachers said no can do.
I projected the images above and asked the kids to give me a guess of how many dozens or how many individual cupcakes can the large container make when the small [real] container can make 1 dozen or 12 cupcakes.
Their guesses were all over the place, ranging from 47 to 994 cupcakes. (We were very careful whether the submitted guesses were in "dozens"or in "individual cupcakes.")
So I did the only thing I knew. I replicated the two cans so the kids could see them physically in the room instead of just on a still photo. Granted the large "can" made from butcher paper was pretty awful.
But, before I asked for another guess at the number of cupcakes, it occurred to me that I wanted to know if kids were better at guessing one and two-dimensional items.
Question 1: How many times taller is one segment than the other?
The two segments below are proportional to the heights of the two cans.
Their estimates:
Question 2: How many times longer is one circumference than the other?
The two circles are proportional to the cans' tops/bottoms.
Their estimates:
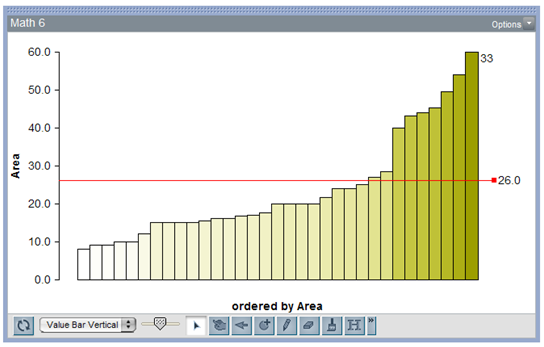
Question 3: How many times larger is the area of one circle than the other?
The two circles are proportional to the cans' tops/bottoms.
Their estimates:
Then, I let the kids — row by row — come up to get a visual check at the paper replicas of the cans. But they may not manipulate the models because I was more interested in seeing the difference between their guesses of the still photo and the physical models.
Their estimates:
If I wrote this post as Dan's 3-Act Lesson, then it was time for Act 2: figure out the volumes of the two cans using their measurements. (Yes, I carry a measuring tape wherever I go now.)
I tried to show the kids equivalent measures whenever possible. We worked a lot with centimeter cubes this year, so this was a rare time that we measured in cubic inches.
And here are some estimates from grown-ups who only saw the left image at the top of post:
(Got more guesses after I printed this: 1,000, 182, 600, 576.)
The straight lines [heights] seemed easiest to estimate. It got a little bit tougher when these lines bend into circles [circumferences] — and there was a large number of over-estimates here. I thought area estimates were pretty good, average of all 33 student guesses was 28.3 (calculated was 26).
The volume estimates, from kids and adults, remained well under the calculated numbers. I don't know what to make of all this. But I kept wondering: Are boys or girls better at making volume estimates? (From my small sample of 33 students, the girls were closer.) How about science teachers? The 3D models helped overall; and I bet if I let the kids do everything but measure the cans, their numbers would be closer. Interestingly, at one point I'd placed the smaller can inside the larger can, and kids who stood nearby kinda gasped. One said, "Oh, you can fit a lot inside."
Thank you, once again, to Andrew for sending me that tweet that started all this! He did a wonderful presentation of 3-Act Lessons to his staff.
Playing with Barbies
I got most of my 20-plus Barbies from eBay and use them well.
I use the Barbies with my 6th graders when we study proportions. I also use them for Barbie Bungee with my algebra students during our unit on linear equations.
The students work in groups of three—one Barbie per group. They take various measurements of Barbie from head to toe; then, they take the exact same measurements of someone in their group.
(I did this activity with math teachers once, and some were concerned that students might not want to be measured. I've done this activity for the last seven years, and if anything, the kids want to volunteer to have their measurements taken.)
I then assign each group one measured body part—Group 1 has “feet,” Group 2 has “waist-to-ankle length,” Group 3 has “head height,” Group 4 has “legs,” etc. Students then take the ratio of their group's assigned human body part to Barbie's. They multiply all of Barbie's measurements by this ratio and sketch their “humanized” Barbie based on these scaled-up numbers.
Below is one of the ten posters that will go up in our school’s cafeteria.
What my kids wrote in their reflections on this activity:
The Barbie was weird. Ms. Nguyen was right—Barbie does look like a freak in human form.
We did a life-sized Barbie and my group got "feet," so that meant she was super tall.
Also, that Barbie project was very fun but creepy at the same time. Barbie was freakishly disproportionate.
Our Barbie's feet were REALLY small.
We did a really fun project with Barbie. I learned a lot about proportions because of it.
People were really creative with their Barbie; our Barbie's name is LOLA! She is cute.
We worked on Barbie and it was weird because Barbie is so weird. My group messed up and now Barbie is messed up—it doesn't even look like Barbie.
We had an insane task! We had to see what Barbie looked like in human form and she's a FREAK! It was pretty fun to do though.
Barbie was a hard, hard, hard challenge. She is so tall. If we did her legs for our body part, it would be soooo long.
Updated 02/09/12