My Other Math Sites

Between 2 Numbers • Chewable Math • Visual Patterns

 

Lessons From the Classroom

Fawn Nguyen Fawn Nguyen

A Routine for Between 2 Numbers

I hadn’t realized the last few entries of between2numbers.com were left blank. They are done now. Thought I’d share a more revised warmup routine of how I’ve used the contents.

I’ll use entry #1 as an example.

I project the two images only and set the timer for 30 seconds for quiet notice-and-wonder. No writing necessary during this time.

I then say, “Before I show you the speed of each of these, I’d like you to discuss with a neighbor what the numbers might be, let’s think miles per hour.” I ask them to write down their estimates [in a journal]. Set the timer for another minute.

I call randomly on two students to tell the class what their guesses are for the snail. Call on two more students for their guesses for the jet. I record these on the board.

Now I reveal the snail’s rate and ask, “Who has the closest guess to this?” Record their answers. This is a good opportunity for students to check their decimal comparison.

Now I reveal the jet’s rate and ask for the same.

I entertain any other related information at this point. I might ask them if they knew what the average speed of a passenger airplane was. Then, I reveal the question.

Okay, this step is important. It saves time writing and fussing over actual quantities, and I find that it helps students focus on the mathematical operation rather than feel anxious about the numbers. I say, “We’re going to let the snail’s rate be A, the jet’s rate be B, and the distance 2,800 miles be C…”

“... Discuss with your neighbor what calculation(s) you would do to find out how much time it takes each object to travel across the US. Just use the letters now. For example, if you wanted to add the two rates, you’d just write A + B.” Set the timer for one minute.

Randomly call on one group to share. Record on the board what they share and ask, “Who has a different solution?” Write down what they say. Continue asking until I have recorded all the different solutions. (Normally, there are usually just 2 or 3 different ones.)

I now take out a calculator and get an answer for each of the solutions shared. I go back to the owners of each solution and ask, “What unit should your answer have?” (If the units were not mentioned earlier.) We discuss the reasonableness of the correct answer.

I’m proud of this site because the routine affords several of these:

  1. interesting facts

  2. estimating

  3. talking and listening

  4. proportional reasoning

  5. unit rates

  6. dimensional analysis

Here is the key. Please share this resource widely, and if you use it, please let me know how it goes.

Read More
Teach Teach

Greenies

Our black lab Mandy is 3.5 years old, weighs a ton, and her breath used to smell like death. Until we started giving her one Greenies a day. My husband orders them from Amazon, he also gets them for our neighbor's small dog Bailey.

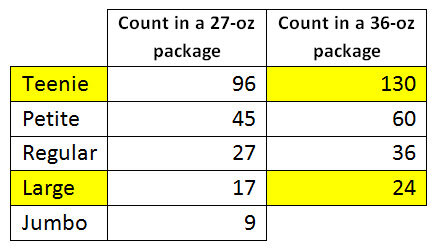
Although both boxes weigh the same 36 ounces, Bailey gets 130 treats in the Teenie size and Mandy gets only 24 in the Large size. This caught my attention which led to this task with my 8th graders who happen to be working with similar shapes. (Like I had planned this all along.)

Greenies are sold in various size packages. I'm interested in the 27-oz and 36-oz.

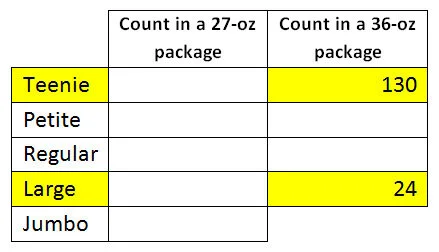
To launch the task, I hold up the 2 treats: 1 Large and 1 Teenie. I tell them that there are 24 Large ones in a 36-oz package, and I want them I guess how many Teenie ones are in a 36-oz package.

both treats

Then I give the students these:

  • The photo of the 2 packages (so they know only the highlighted information in the table above).

  • Each group of 3 students get two real treats: 1 Large and 1 Teenie.

In return, the students need to give me these:

  • A 2-dimensional outline (with dimensions labeled) of what a Petite, a Regular, and a Jumbo may look like. For example, these are the actual outlines of the Large and Teenie. They may write down the thickness also.

  • A completed table with the missing counts filled in.

Highlights of this task:

  1. Kids use some known information to construct new information. They use modeling to figure out what the other sizes may look like and how many of them would fit in a 27-oz or 36-oz package.

  2. It's kinda messy and weird. While the kids can measure whatever lengths of a treat, how do these numbers translate into the mass of each treat?

  3. It's good to work with solid objects instead of just flat polygons when learning similar shapes.

  4. The reveal (Act 3) of something like this is always a lot of fun. Not only the reveal in the count per package, but also how close their outline sketches are to the actual treats when I bring in the Petite, Regular, and Jumbo.

  5. How much does a 36-oz package cost?

  6. Is the Jumbo a shot in the dark? Would kids think to ask me for the size of the dogs? How does this help, if at all?

Read More