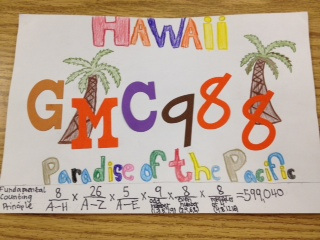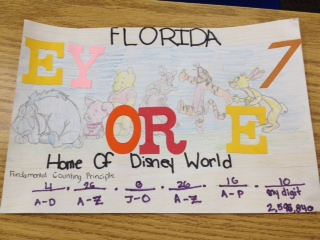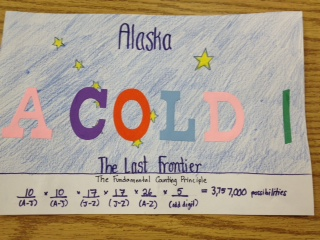Designing License Plates

Yesterday I saw this question in the 6th grade workbook:

Use the Fundamental Counting Principle to find the total number of outcomes in each situation...

12. a license plate that has 3 numbers from 0 to 9 and 2 letters.

Then an idea popped into my head that my kids could design these license plates. We've covered sample space already, and I brought up the Fundamental Counting Principle last month when the Mega Millions jackpot soared to a record high of $640 million.

I gave them instructions for the layout.

I let them research the state and start a rough sketch in their math journal.

I asked them to record on the white board what letters and digits they needed me to cut for them.

I gave each student a 8" x 12" white construction paper, reminded them this was the only one they'd get from me.

I told them their homework was to complete at least the background drawing.

I gave them one class period this morning to glue the letters and digits onto their plates. They checked to make sure their calculations were correct for the sample space.

I'm very pleased with how well these license plates turned out with only two class periods used. We wrapped up the activity by figuring out the sample space for California plates, but I also pointed out that not all possibilities could be used or some people would be driving around with plates like "1ASS29" or "2FAT46."

Unders and Overs

Here's where I got the idea for "Unders and Overs."

Yesterday, my colleague alerted me that we were almost two chapters behind in our 6th-grade pacing calendar. I'm always behind in this annoying and demanding calendar, but never quite this far back. So, just like that, I told the kids we were done with Chapter 8, and let's move on to Chapter 9 — Probability!

What's the best way to start a new unit? We play a game, of course.

I ask the kids to take out a blank sheet of notebook paper, place it on their desk in a landscape layout, divide the paper into thirds, and mark each section like this:

I give each kid a bag of centimeter cubes. (We use these often for all sorts of things.)  I tell them to take out only FIVE cubes—and this is their money. The remaining cubes in the bag represent the dealer's money. I am the dealer. I tell them to be honest—because it sucks to cheat—and they may not borrow and will have to sit out if they lose their five cubes.

I explain the game: I will roll two dice; if the sum is under or over 7, then I—the dealer—pay them even money, and if the sum is equal to 7, then I pay them 3 to 1. I do a few examples to make sure they understand. I trust them to reach into the bag to take out the dealer's money if they win and to put money into the bag if they lose. They lose when they place a bet on a space that I did not roll.

I check across the room to make sure they place their bets before seeing the dice roll. These are 6th graders—they are adorable, but I wouldn't put it past them to lie about bets!

First roll: we get a 2 and a 5, so the sum is 7... the kids cheered! The second roll was under 7, they roared! The third roll was over 7, they went nuts!

They are having so much fun! I pause to remind them to think about the math. What math? And that's okay right now. The ones who are winning are betting more cubes. Leo puts one cube in each of the three spaces; Arthur tells him, "I don't think that's a good idea."  Melanie is betting on all three spaces anyway; she says this will give her a better chance of winning.

The math will turn up eventually. Let's have fun right now.