My Other Math Sites
Lessons From the Classroom
A Lazy Teacher's Version of Block Game
I love the "Block" game that my colleague Erin has shared with me. Erin found it at Maria Anderson's post. It looked familiar, turned out it was one of Elizabeth's #made4math posts.
There's just this one BIG problem: I dread making games that require a bunch of little game pieces!!
Erin must have spent hours typing up the 36 math expressions for the distributive game, wrote the 36 answers on the back, made 18 copies — for 36 kids to play in pairs — and cut each copy into 36 little game pieces. I felt bad using them because I didn't help at all.
Whenever I borrow stuff I'm extra careful with it, so I kept reminding my kids to be gentle with the pieces, to not lose any of them, to not write on them, and don't even breathe on them!
Because the algebra kids really liked the game, I thought, Okay, I'm going to make one for order-of-operations for my 6th graders! I lasted all of five minutes.
Then an idea popped into my head that requires NO GAME PIECES AT ALL!!
I made two changes:
Instead of a blank 4x9-grid game board, I number the spaces from 1 to 36.
Instead of typing up 36 questions and 36 answers (photocopied back-to-back) and cutting them out, I use KUTA to generate a worksheet with 36 questions — takes 1 minute. KUTA also automatically generates the answers. I print the questions and answers back-to-back.
So, this would be all that is needed for two players:
1 game board
2 worksheets (36 questions in front, 36 answers in back) — one for each person
2 different game markers
You can put the game boards and worksheets into plastic sleeves — or laminate them — to protect and re-use them. I'm just going to protect the game boards but leave the worksheets as consumables, this way kids can write on them to do their math work.
The game is similar to tic-tac-toe 4-in-a-row. Maria's directions in pdf.
Yes, kids can cheat in this game because the answers are in the back of the worksheet or in the back of each game piece. But I make it clear that each person needs to show his work to the opponent.
Cheaters cheat themselves. I don't care.
Staircases and Steepness, Continued
This happened Thursday.
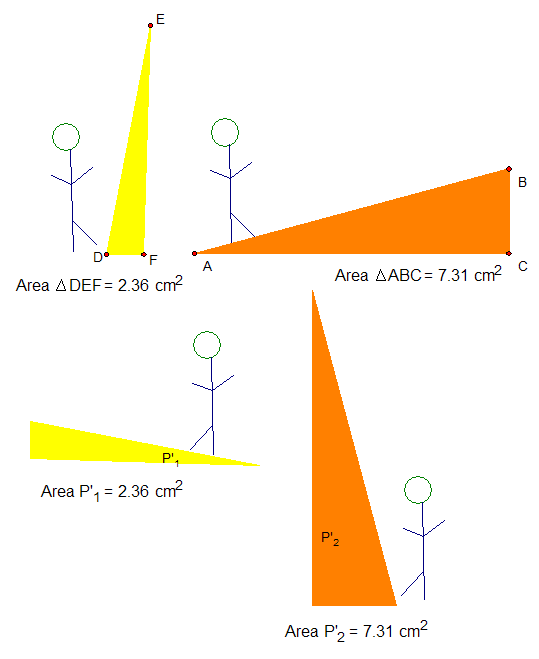
By Friday morning the kids who did "base times height" learned that these numbers didn't match up with the steepness ranking. They said, "That just gives you area."
So I made these sketches, and hopefully the kids understood why finding area wasn't the same as finding steepness.
Those who did not do "base times height" shared what they'd calculated for steepness:
Because almost everyone got the correct steepness ranking the day before, they knew their homework calculations had to match the order, with staircases B and E yielding the same number.
Rapha: My dad helped me. I learn that the steeper it is, the number gets closer to zero.
Jocelyn: I measured one of them wrong. Did I just get lucky then?
Ryan: I tried base divided by height first, then I changed my mind to height divided by base because it made more sense for the numbers to go up instead of down... if it's gonna get steeper.
Matt: My base minus height did not work!
Arthur: Rapha's kinda the same as Ryan's, except backwards. And if you add her step widths, you get the base.
I was on cloud nine. Then I finally said the word slope, but I never said "rise over run." We ended class with this video "Tutorial — Measure Slope Steepness" by Bruce Tremper, Director of the Utah Avalanche Center.
We had a busy but fun Friday as it was also our 3rd quarter PFO-funded Einstein pizza party. Luckily my prep period is right before lunch to allow me to leave campus to get the 8 pizzas at Costco. The weather was gorgeous and we had 10 minutes left of geometry, so I took the kids outside to play Fizz-Buzz. If you've never played Fizz-Buzz with your kids, then don't start unless you want them to constantly pester you to play the game, even when there's only a minute left of class.