My Other Math Sites

Between 2 Numbers • Chewable Math • Visual Patterns

 

Lessons From the Classroom

Fawn Nguyen Fawn Nguyen

A First Grade Lesson Using Vertical Whiteboards

As we wrapped up our book study of Peter Liljedahl’s Building Thinking Classrooms, and in my role as TOSA (teacher on special assignment) I do not have a classroom of my own, I asked one of our first-grade teachers if I may facilitate a thinking task using vertical whiteboards with her students.

To supplement the teachers’ classrooms with more whiteboard space, I reached out to Wipebook for durable dry-erase chart paper surfaces (with grids on one side!). The reusable Flipcharts they sent were the perfect tool to use over her glass doors and windows! They can easily be removed and reused as many times as you want — an eco-friendly solution to reduce paper waste. Our district has also purchased whiteboard easels with adjustable heights.

The teacher already had her groups paired up with their “thinking partners.” Each whiteboard space was labeled such as “Blue 1 and 2” so the students knew where they would be working.

We had the students sitting on the carpet area for me to launch the task. I taped this flower image on the board and asked how many circles they saw. They said seven.

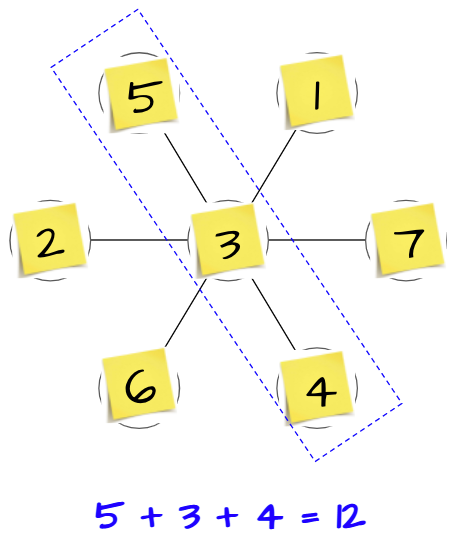
Then, I counted out along with them seven sticky notes, marked from 1 to 7. This great Flower Petal Puzzles thinking task is from Dan Finkel, founder of Math for Love. The intent of the task was for students to write the numbers inside the circles/petals and to keep track of numbers they have used by crossing them off at the bottom of the page. Dan also suggested using counters. However, I wanted the students to do these vertically, so counters would not work, and writing numbers in and erasing them is challenging and cumbersome, especially for young students. The use of sticky notes was really key in helping students stay focused on the task because it was easy to swap out numbers and keep their brains moving.

I called up one student at a time to place a numbered sticky note into an empty petal without further instruction or stating what the goal was. When there was only one space left, I said it was my turn and placed the number in. I wish I had taken a picture of the board at this point. But since I didn’t, below is a picture of the flower with randomly placed numbers. I then told them these three petals are connected and asked them for the sum and wrote the equation.

We found the sum of the other two groups.

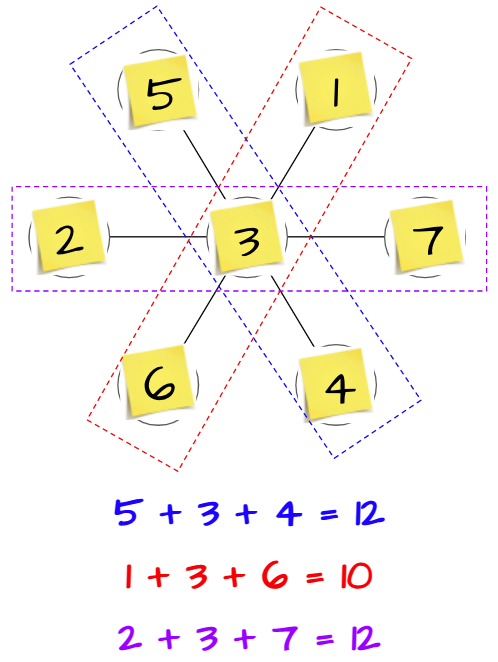
It was not until then that I told them the challenge of the task was to have all three sums be the same. And that the sum is 10. So off they went with their thinking partners to their whiteboards! 

Sure enough one pair got the solution within 5 minutes, and we asked them to keep their equations (not erase them), and to do the next challenge which was to get a sum of 12 for all three equations. Some time later, all of the groups except for two got the 10 puzzle. We came over and applauded them for their perseverance and asked if they would like a clue. They nodded and we let them know to place the number 1 at the center of the flower. When this group got the solution with the hint, the girl excitedly said to me, “This is a lot of fun!”

I tweeted this out later as truly it was the best hour with first graders for me. So much perseverance, so much thinking, so much fun. The groups were in different stages (finding sums of 10, 12, and 14), and two groups ended the hour working on the “ultimate challenge” of creating their own puzzle using a 9-petaled flower.  

Updated 04/11/2022

Read More
Teach Teach

Rigid Transformations

My 8th graders are learning about rigid transformations. I want to add a bit more complexity to what our book is asking the kids to do. For example, the book is having them reflect a shape mainly across the x-axis or y-axis, or on a rare occasion, reflect it across "the horizontal line that goes through y = 3." Well, right before this chapter, we've been working with writing and graphing linear equations, so I want kids to reflect a shape across any line, including one that may cut through the shape itself.

The book surprisingly has very few examples and exercises with rotations. And from what I can find, all these rotations happen about the origin or about a point coinciding with one of the vertices of the shape. Again, I want kids to be able to rotate a shape about any point, including one that's inside the shape. (I used a playing card — number 7 works well because it's asymmetrical — poked my pencil through it as the center of rotation, and turned the card. I think this helps them see what I keep referring to as the pivot or anchor point.)

Then I give each student this task:

  • Draw a shape that has between 5 to 8 sides with no curved edges.

  • Transform your shape through at least 3 rigid transformations of rotation, translation, and reflection — in any order.

  • On grid paper, give your teacher your complete work on this, including the written directions for the transformations.

  • On grid paper, give your teacher only the original shape and the written instructions. Your teacher will give this paper to a random classmate to follow your written directions to arrive at the intended location of the final image.

For students who want more challenge, they may ask for a copy that has just the original shape and its final image without the written directions. The task will then be to figure the appropriate transformations that connect the two images.

I really believe that it's good practice to always give kids more than what we believe they can handle. Let kids tell us when it's too much for them — and we find out soon enough. An ounce of struggle on something hard is worth a pound of completion on something easy.

Read More