My Other Math Sites
Lessons From the Classroom
Four Square and Other Questions
One afternoon during recess I noticed that the Four Square grid at our school had been enlarged. Naturally I yelled out to the kids, "Hey kids, when did they make this larger? I wonder what percent increase this is. What do you think?”
Taking a nanosecond pause from their game, they yelled out their estimates, anywhere from 50% to 95% increase. One kid said, "I love that you're asking us a math question at recess time." I went back out to the playground during my prep with a couple of yardsticks to find the answer to the question I'd posed. When my 6th graders came into class the next period, I told them what I'd wondered about during recess and wanted each one of them to give me an estimate of this percent increase. We walked back out to the Four Square, and I allowed them five minutes to do whatever they needed to get a good estimate.
Once back into the classroom, I asked them to write down their estimate of the percent increase on a small slip of paper. I then asked, "What exactly was I looking for? Percent increase in what? I really didn't say and you didn't ask me to specify either."
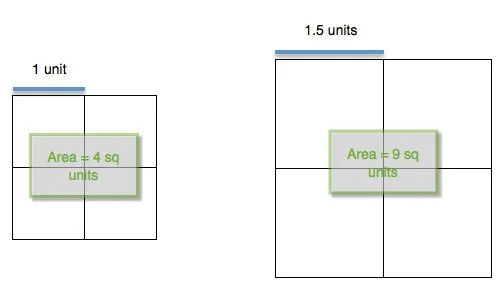
We've been working A LOT with perimeter and area of rectangles, so most of them said that they'd thought I'd meant the percent increase in area. So I told them I did mean area but I was intentionally vague just to see if anyone would ask — and Four Square is so much about occupying the inside space. This question prompted me to ask them more questions about increase in perimeter versus increase in area. I had them draw squares (or rectangles) on grid paper and explore the changes in area when the perimeter is doubled, tripled, or by some x factor. We remind ourselves that area is two-dimensional and why area units are always "squared." I asked them how they would figure out the percent increase in area. They told me I needed to measure the length and width of the old Square (black outlines), then do the same for the new one (white outlines). They also agreed that I could just find the area of 1 square, then multiply this by 4 to get the whole thing. This suggestion prompted me to ask them, "Well, do I need to compare the area of the whole 4-square grid of new to old, or just the area of 1-square of new to old?" So we just drew some squares to show that comparing the areas of just one square each: large to small is 2.25 to 1.0, this is a percent increase of 125%. And comparing the areas of each entire 4-square grid: large to small is 9 to 4, which also yields a 125% increase.
This brief noticing and wondering yielded a fruitful discussion and it was something that was part of their environment, their playground. By the way, the answer is 118% increase in area for the Four Square. The closest written estimate was 115%. Of course this launched us into a brainstorming session of questions that they have about their surroundings. Stuff that we can apply math to answer the questions. I reminded them not to worry about answering the question. Just ask it. Then I couldn't stop them from sharing. (These 6th graders are away at Outdoor School, so I have to wait for them to return next week for us to try and answer some of these questions. They will also be jotting down more questions that may come up during the week.)
How much time does my brother waste in his room for a year?
How many gallons of water do we use if we take 5-minute showers a day?
How much does this cost?
How much power is needed to charge all the devices in the house for a year?
I wonder how many pencil tips I break each year, and if added end-to-end, how long would this be?
What is the average amount of money each teacher at our school spends on supplies in a school year
How many eggs does a chicken lay in United Kingdom?
How much pollution does the average car put into the air monthly?
How much time do the students in this class spend on YouTube in a month?
How much time do we spend on homework during the school year?
How much money does our school lose when students are absent?
How long does my hair grow in a month?
I always wondered how much bigger is the big basketball hoop compared to the small one.
How many pounds of food do kids waste in the cafeteria in a month?
How much gas does my mom burn while she is driving?
I wonder how much gasoline our 3 school buses use each year.
How many "perimeters" do we do in a year in PE?
How much money does Mrs. Nguyen spend on Oregon Ducks' games?...
And this one breaks my heart.
How long would it take to end poverty?
The Right Question Institute
From www.aish.com:
Isidore Rabi, winner of a Nobel Prize for physics, was once asked why he became a scientist. He replied: “My mother made me a scientist without ever knowing it. Every other child would come back from school and be asked, ‘What did you learn today?’ But my mother used to say, ‘Izzy, did you ask a good question today?’ That made the difference. Asking good questions made me into a scientist.”
A week ago my superintendent, principal, and 7 of us teachers attended a full day workshop The Right Question Institute in LA. Luz Santana and Dan Rothstein, authors of Make Just One Change, facilitated a worthwhile and engaging session, so I just want to share some highlights and my takeaways from it.
Highlights
(Some of these might be direct quotes. I’m just writing from my notes.)
Not knowing what to ask is the fundamental obstacle to participating and therefore to learning.
The skill of question formulation is the single most powerful renewable source of intellectual energy.
How can we easily develop students’ question formulation skills? It’s simple. But simple does not mean simplistic — it means doing it so everyone can access it.
Six components of the Question Formulation Technique (QFT):
A question focus — the teacher gives a prompt related to topic currently being covered in class, prompt can be visual. It should be a statement or phrase and not as a question. The simpler, the better.
Producing questions — in small groups, students share questions that they have related to the question focus (prompt), one person records on large poster paper or whiteboard. But before starting, everyone is reminded of these rules:
Ask as many questions as you can.
Do not stop to discuss, judge, or answer any question.
Write down every question exactly as it is stated.
Change any statements into questions.
Categorizing questions as “open” or “closed.”
Prioritizing questions — choose 3 most important questions from list, pay attention to the question focus.
Next steps — what’s one way you could use your priority questions?
Reflecting — what did you learn and how did you learn it?
Takeaways
Luz and Dan are really lovely people. Warm, hard-working, fun. Their book — and this Institute — mark the arrival of a twenty-year journey for them! (Arrived, yes. Settled, no.)
This task of having kids ask their own questions is not unlike Act 1 of a 3-Act math task that many of us are familiar with.
But the QFT process can be used — and is used — in a variety of academic disciplines and in communities outside of school. (Their journey actually began when they worked on a dropout prevention project and heard from the parents who were not coming to the school meetings because they “don’t even know what to ask.”)
This is another powerful structure that empowers students when asking questions becomes a natural tool for them. They think more critically because the QFT process helps them hone in on their questions. Dan and Luz categorize the learning of asking questions as going from divergent thinking to convergent thinking, then that last component of reflecting is metacognitive thinking.
Teachers and students will get better at implementing the QFT. It’s building classroom culture, so it takes time.
We’re doing this already with our students to some degree with varying expertise. Maybe we just need to be more intentional about it. Give it a name.
If not, perhaps Make Just One Change.