My Other Math Sites
Lessons From the Classroom
Four Square and Other Questions
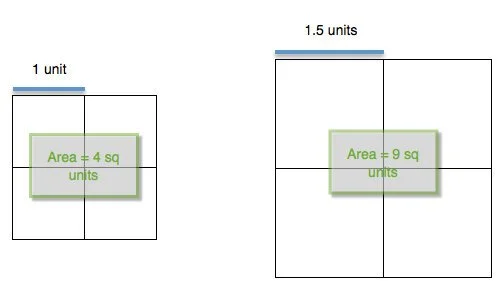
One afternoon during recess I noticed that the Four Square grid at our school had been enlarged. Naturally I yelled out to the kids, "Hey kids, when did they make this larger? I wonder what percent increase this is. What do you think?”
Taking a nanosecond pause from their game, they yelled out their estimates, anywhere from 50% to 95% increase. One kid said, "I love that you're asking us a math question at recess time." I went back out to the playground during my prep with a couple of yardsticks to find the answer to the question I'd posed. When my 6th graders came into class the next period, I told them what I'd wondered about during recess and wanted each one of them to give me an estimate of this percent increase. We walked back out to the Four Square, and I allowed them five minutes to do whatever they needed to get a good estimate.
Once back into the classroom, I asked them to write down their estimate of the percent increase on a small slip of paper. I then asked, "What exactly was I looking for? Percent increase in what? I really didn't say and you didn't ask me to specify either."
We've been working A LOT with perimeter and area of rectangles, so most of them said that they'd thought I'd meant the percent increase in area. So I told them I did mean area but I was intentionally vague just to see if anyone would ask — and Four Square is so much about occupying the inside space. This question prompted me to ask them more questions about increase in perimeter versus increase in area. I had them draw squares (or rectangles) on grid paper and explore the changes in area when the perimeter is doubled, tripled, or by some x factor. We remind ourselves that area is two-dimensional and why area units are always "squared." I asked them how they would figure out the percent increase in area. They told me I needed to measure the length and width of the old Square (black outlines), then do the same for the new one (white outlines). They also agreed that I could just find the area of 1 square, then multiply this by 4 to get the whole thing. This suggestion prompted me to ask them, "Well, do I need to compare the area of the whole 4-square grid of new to old, or just the area of 1-square of new to old?" So we just drew some squares to show that comparing the areas of just one square each: large to small is 2.25 to 1.0, this is a percent increase of 125%. And comparing the areas of each entire 4-square grid: large to small is 9 to 4, which also yields a 125% increase.
This brief noticing and wondering yielded a fruitful discussion and it was something that was part of their environment, their playground. By the way, the answer is 118% increase in area for the Four Square. The closest written estimate was 115%. Of course this launched us into a brainstorming session of questions that they have about their surroundings. Stuff that we can apply math to answer the questions. I reminded them not to worry about answering the question. Just ask it. Then I couldn't stop them from sharing. (These 6th graders are away at Outdoor School, so I have to wait for them to return next week for us to try and answer some of these questions. They will also be jotting down more questions that may come up during the week.)
How much time does my brother waste in his room for a year?
How many gallons of water do we use if we take 5-minute showers a day?
How much does this cost?
How much power is needed to charge all the devices in the house for a year?
I wonder how many pencil tips I break each year, and if added end-to-end, how long would this be?
What is the average amount of money each teacher at our school spends on supplies in a school year
How many eggs does a chicken lay in United Kingdom?
How much pollution does the average car put into the air monthly?
How much time do the students in this class spend on YouTube in a month?
How much time do we spend on homework during the school year?
How much money does our school lose when students are absent?
How long does my hair grow in a month?
I always wondered how much bigger is the big basketball hoop compared to the small one.
How many pounds of food do kids waste in the cafeteria in a month?
How much gas does my mom burn while she is driving?
I wonder how much gasoline our 3 school buses use each year.
How many "perimeters" do we do in a year in PE?
How much money does Mrs. Nguyen spend on Oregon Ducks' games?...
And this one breaks my heart.
How long would it take to end poverty?
Driving Them Nuts
I'm proud of my students. I'm proud of what we do in room 15. My classroom. My home away from home for the last 11 years. These bopping teenagers, sullen one minute bubbly the next, hormonal but invincible. They don't all love math like I do. (Not everyone loves college football, but we get along.)
What is happening in room 15 is the loud and proud math culture that we have set in place. We build it from day one — then we continue to do, say, and write stuff to sustain and strengthen the culture because we know our behaviors are our best evidence that this culture exists.
Here's one piece of that evidence:
Her frustration resulted in her loving the problem. Her last sentence is an enormous celebration of how much we honor the process of problem solving. Her classmates had their own reflections — short snippets of how they engaged in the problem.
They worked hard on the problem because it was driving them nuts. It's not unusual to hear kids blurt out, "This problem is making me crazy!" Or, "I won't be able to think about anything else until I get this!" Now, they've owned it. This isn't about a letter grade any more; and it certainly isn't about me.
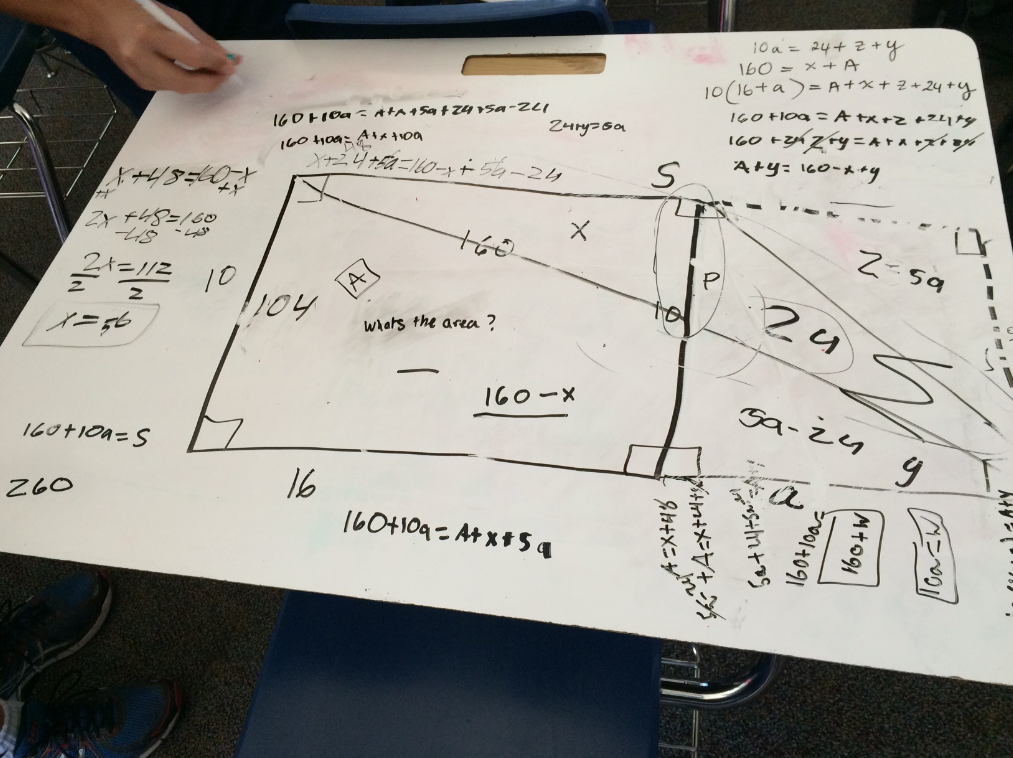
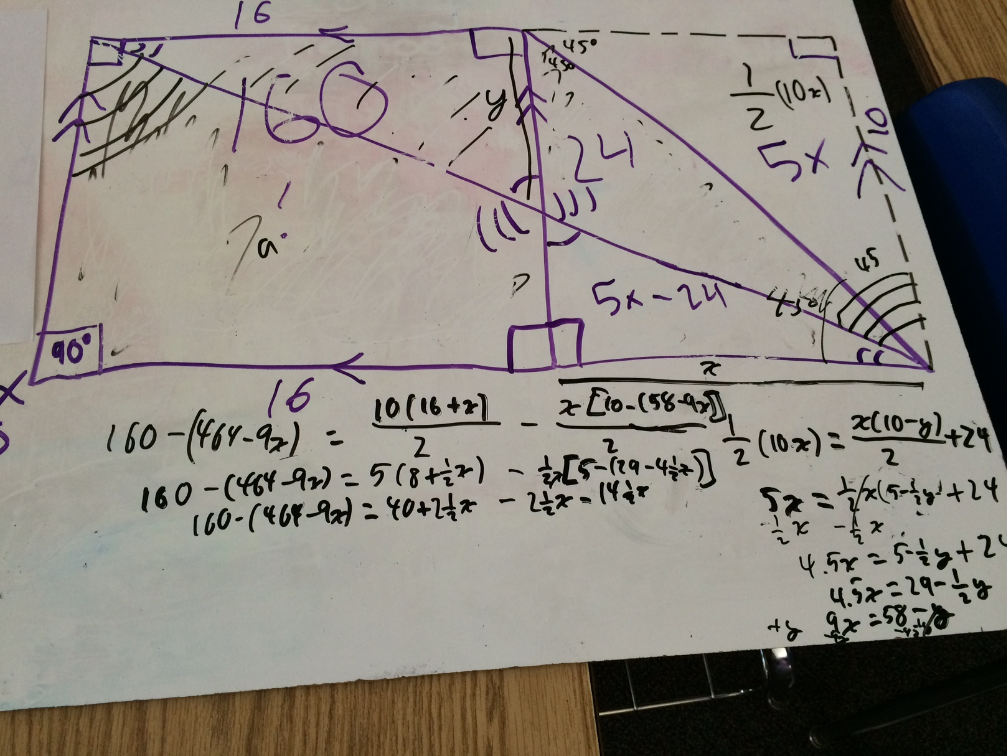
This was the problem they'd worked on.
The Missing Area
A 10 by 16 rectangle is attached to a triangle as shown below. If the purple section is 24 square units, then what is the area of the yellow section of the rectangle?
John Golden, GeoGebra extraordinaire, created an animated gif of this problem.
Mike Lawler solved this problem using similar triangles.
Area of a Circle
After finding the formula for the circumference of a circle, my 6th graders were ready to work on finding the area of a circle.
I asked them to draw a circle on notebook paper, any size, but not too small. Then I gave each a centimeter cube to trace one face onto their paper to remind them how much the area of one square centimeter covered. (You can see it drawn on top right pic below.)
Question 1: Give me a guess — only by looking — what is the area of your circle, in square centimeters? Please write that number on your paper, label it "guess."
Question 2: Now use whatever tools you need, give me a better answer. I know some of you already know the formula for the area of a circle, but you may not use it unless you can tell me where it came from. (No one even tried.)
I can't tell you how happy I was to see all the different ways the the kids had tried to approximate area. Their perseverance humbled me. A few students drew triangles, knew to use "base times height divided by two," but erroneously used radius as height.
Last week I was reading Mimi's post about estimating area of circles, and Sue VanHattum reminded me of the rectangle model in her comment.
I had the kids fold their circles like this.
They cut out the pieces — turning every other piece 180 degrees — and glued them together. Cristian said, "First we had a circle, then triangles, then a rectangle. That's crazy!"
Never once did I answer any of the questions. I just asked them. I began with, "What is the area of this rectangle or parallelogram?" Step by step, as a class, the kids walked this equation all the way to Area = pi x radius^2.
This morning, two days after the activity, I did a My Favorite No to see if they remembered: 31 out of 33 students got the correct circumference formula; 24 of 33 got the correct area formula. Bonus if they showed me how the rectangle model helped explain the area of a circle.
Follow Up on Friday Bubbles
My 6th graders had a blast last Friday blowing bubbles.
Upon their return on Monday, I asked for ten groups to volunteer just one set of their circumference and diameter numbers. Then I asked, "What is the relationship between these numbers?" Some quiet mumbling, then just quiet. I asked again, "I have these 10 sets of numbers. What should I do with each set of numbers to see if there's a relationship between them? I want you to use your calculator to do something with these two numbers and find out for me."
They were busy punching in numbers. After a few minutes...
Me: What are you punching into your calculator?
Matt: I'm dividing the numbers.
Me: Why divide? Why not add or subtract? Or multiply the numbers?
Matt: Adding and subtracting don't tell you anything. Just doesn't make sense.
Sophia: The circumference is always bigger than the diameter. So I think I want to know how many times it's bigger.
Me: Class, do you agree that we should divide circumference by diameter? (Lots of nods around the room.)
While they continued with their own bubble numbers, I filled in the "relationship" column for the 10 volunteered sets from earlier.
They were skeptical — didn't know what to make of the "relationship" column. I said, "I think measuring a bubble imprint with a string is not easy. It was fun to blow bubbles, for sure. But what about it that may have affected how your numbers came out?"
Their answers:
The bubbles were sometimes oval shaped.
Hard to keep the string perfect.
It can get messy!
Maybe some people didn't measure the widest part.
Maybe they measured in centimeters for one part and inches for another.
It was so much fun! (I can always count on a random answer.)
I said, "Because our bubble numbers could use some help. Let's do a clean run through this again, this time using paper and pencil."
I asked them to draw two to three different sized circles on notebook paper — measure the diameter and circumference of each one. I showed them how to "walk" the string around the circle for better accuracy — press and let go, press and let go... They knew that if they started from one end of a diameter, walked the string around the circle, to the other end of the diameter, then they just needed to multiply this by two to get the circumference.
I asked them to find the "relationship" number again for each circle.
The paper in top row, left, reads: All of them are around 3, which is close to pi. Other papers didn't include observations or conjectures, and a few wrote they weren't so sure. But when we shared ALL the "relationship" numbers that the class had — over 60 of them as each student did at least 2 circles — and they were pretty well convinced that the diameter was "about 3 times longer" than the diameter!
I showed them this very short video to reflect the simple work that we did.
Next up, we are going to find the AREA of a circle!!!!!!!
Circles Galore
This lesson is from MARS. Using graphics from the original source, I created this recording sheet.
But instead of passing out the worksheet and starting right in like I had intended, I placed the stack in my desk drawer and decided to ask the kids to follow my instructions to create the diagrams.
I gave each kid one sheet of unlined paper and a compass. These were my instructions to them, and I followed along also.
Put a dot in middle of paper.
Draw a large circle using the dot as its center.
Draw in the diameter.
On this diameter, mark half the radius. (I could ask them to bisect the radius, but to save time, we just estimated "half" using a ruler.)
Now draw a circle, centered at this half-radius mark, using a radius half that of the original circle, draw two adjacent circles along the diameter.
Shade in the outside of the two small circles — their drawings should now look like Stage 1 on worksheet.
We stopped here, and I asked Question 1) What fraction of the large circle is shaded? They quietly did their thing.
After seeing about half of the kids finished answering this question. I said, "I know not everyone is done with #1, which is perfectly okay, but I'm going on with my instructions because some people are done, and I need you to follow along. Then if you need to, you can go back to #1."
I repeated directions 4 and 5 above, and before I asked Question 2, Josh said, "What fraction is shaded now?" They went to work again.
I then repeated the instructions to get their drawings to Stage 3. However, our compass can't make a circle smaller than 0.5-inch radius, so we freehanded them in. Everyone knew next came Question 3) Now, what fraction is shaded?
And Josh immediately asked, "Are we doing this again, make even smaller circles?!" We drew in the next 16 shaded circles for Stage 4.
You guessed it. Question 4) What fraction of the large circle is shaded? I asked them to work alone on the questions, but that they would have a chance to discuss with other classmates during the last 15 minutes of class. They plugged away.
Then the talking began; and there was a lot of it, so I started recording their conversations. I was more interested in those who did not get 1/2 for Question 1. I happened upon Zach telling his two classmates that the answer was 2/pi:
Did you catch what Zach said? He reasoned that (16*pi) + (16*pi) = 2*pi*32 by saying "You can't get rid of stuff because we haven't done any mathematical operation to get rid of pi." I was so glad this came up! Sometimes I feel a wrong answer is just as important as the correct one.
(But I thought it was funny too how Slater reacted, "That's wrong." Then there was peer pressure, "He made me change my answer." And there was alleged copying. Then there was, "Taj showed me the way." I will miss this class.)
Daniel started the discussion with this group.
The "formula" that Daniel had trouble articulating was never written on his paper, it was all in his head. Then I noticed that he'd carried his calculations to stage 8! I was so pleasantly surprised by this that I was speechless.
Class ended and everyone agreed that the answer to question 1 was 1/2.
I passed out the worksheet above for homework, asking them to try to figure out the answers for stages 2 through 4 if they hadn't already, then to give stage n a try if they had time. Daniel never saw the worksheet to know that I'd wanted him to keep thinking of the pattern, but he was already heading there on his own.
Tomorrow we'll finish out this lesson, but I wanted to capture what we've had so far before my amnesia sets in.
Some thoughts:
When I search for lessons/activities for my kids to do, I always search for lessons "recommended" for kids at least one grade level above mine. Meaning, I look under 9th and 10th grade activities for my 8th graders. Why not? I could always work back from there.
I remember adding "stage n" to the worksheet just because there was some left over space at the bottom. This made Daniel happy.
I'm glad I had them draw the circles. This was a last minute decision that paid off — they made pretty sketches!
I learn that my kids are smarter than I am. (But let's not tell them this.) Daniel's "equation" was so elegant that he could do all of it in his head.
Stage n, if we get it or not tomorrow, is icing on the cake. I feel pretty full.
Speaking of stage n. What do you think? Is there a limit that we are approaching?
Investigating Area With Paper Folding
Last Thursday was a half-day for students because we had an open house at the event. I decided it was a good day for my geometry students to do some paper folding. I gave each student about five sheets of hamburger patty paper and these instructions:
Task 1: construct (by folding) a square that is 1/4 the area of the original square.
Everyone got it except Daniel, who didn't follow instructions and constructed a rectangle with 1/4 the area. The kids jokingly gave him a hard time. I reminded the class that Daniel's left arm was still in a cast, so squares and rectangles were the same to him.
Task 2: construct a triangle that has 1/4 the area of the original square.
Again, no problems. Everyone folded the same way.
Task 3: construct another triangle, still 1/4 the area of the original, but this triangle may not be congruent to the one you created in Task 2.
Some time passed, but not too long before Slater got it, and Zach did. They shared it with the class.
Task 4: construct a square that is 1/2 the area of the original square.
Easy-peasy.
Task 5: Construct a square that is 1/2 the area of the original square—the same instruction as Task 4—however, it must be "oriented differently."
Then I went to sit down, put my feet up (okay, figuratively speaking only), drank some water, and peacefully watched as my students slowly but surely mangled up their papers trying to create this square. They asked for more paper, and I gave them more.
Austin: What do you mean "oriented differently"?
Me: Its orientation is different.
A: That didn't help...
M: I'm not here to help you. Not today.
Zach, waving his folded paper above his head and proceeded to walk up to me: Oh, I got it!
M: No, you don't got it. Sit down.
Josh: I got it!!
M: No you don't.
J: But you didn't even look at my paper.
M, pretending to look: There, I looked.
I watched with satisfaction as everyone struggled with Task 5.
The kids know I live for moments like that. They are stuck, and they have to think hard.
Even Slater, a self-proclaimed math prodigy (who had elevated himself to "academic prodigy" since then), was quiet and used his pencil to calculate on paper. Even Bobby—who once claimed that he and Slater should get the same IQ score if tested—sat quietly, arms to his sides, staring at the patty paper.
The bell rang. I told them to work on it for homework, and the hint was "right triangle."
Alex: Someone will look it up online, Mrs. Nguyen.
Me: That's their loss.
For the next day, we did Task 5 together. The smiles returned to their faces. I love teaching.
Updated 03/26/12
I got this activity from a workshop. At bottom of worksheet:© 2008 by Education Development Center, Inc. from The Fostering Geometric Thinking Toolkit. Portsmouth, NH. Heinemann