My Other Math Sites
Lessons From the Classroom
Staircases and Steepness, Continued
This happened Thursday.
By Friday morning the kids who did "base times height" learned that these numbers didn't match up with the steepness ranking. They said, "That just gives you area."
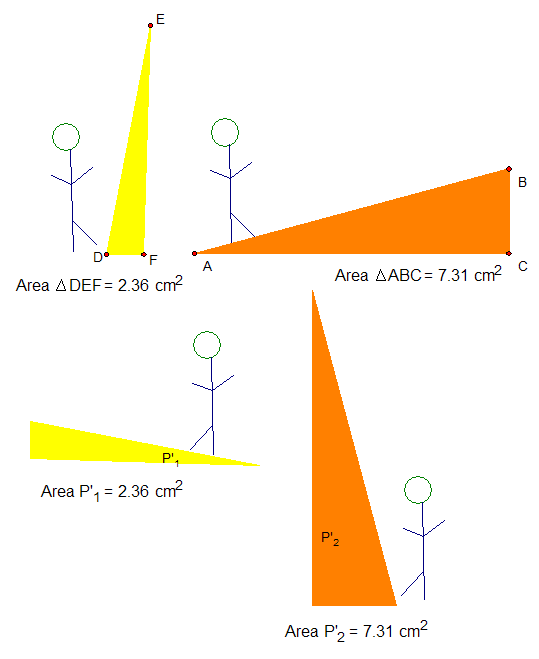
So I made these sketches, and hopefully the kids understood why finding area wasn't the same as finding steepness.
Those who did not do "base times height" shared what they'd calculated for steepness:
Because almost everyone got the correct steepness ranking the day before, they knew their homework calculations had to match the order, with staircases B and E yielding the same number.
Rapha: My dad helped me. I learn that the steeper it is, the number gets closer to zero.
Jocelyn: I measured one of them wrong. Did I just get lucky then?
Ryan: I tried base divided by height first, then I changed my mind to height divided by base because it made more sense for the numbers to go up instead of down... if it's gonna get steeper.
Matt: My base minus height did not work!
Arthur: Rapha's kinda the same as Ryan's, except backwards. And if you add her step widths, you get the base.
I was on cloud nine. Then I finally said the word slope, but I never said "rise over run." We ended class with this video "Tutorial — Measure Slope Steepness" by Bruce Tremper, Director of the Utah Avalanche Center.
We had a busy but fun Friday as it was also our 3rd quarter PFO-funded Einstein pizza party. Luckily my prep period is right before lunch to allow me to leave campus to get the 8 pizzas at Costco. The weather was gorgeous and we had 10 minutes left of geometry, so I took the kids outside to play Fizz-Buzz. If you've never played Fizz-Buzz with your kids, then don't start unless you want them to constantly pester you to play the game, even when there's only a minute left of class.
Staircase and Steepness
AHHHH, I love how this lesson has turned out so far!!
Today was our 3rd day of State testing, and because I have 8th graders for homeroom, we still have three more days of testing next week. Ick.
I didn't want to cram/review again with my 6th graders today, so I thought of doing a lesson on "steepness" (adapted from Swan and Ridgway).
I began the lesson by showing a bunch of images, like these, and asked,
What do you see?
Kids' responses: going down, going up, all using their legs, exercise, at an angle.
Here’s the lesson. I purposely wrote it as if it were unfinished because I didn't want it to end on my terms. I wanted the kids' conversations and discoveries to guide me to closure, if any.
Question 1: Without measuring the staircases, put them in order of "steepness," starting with the shape with the least "steepness."
Question 2: Explain how you came up with your ranking in #1. Because you were asked NOT to measure, what "tools" or strategies did you use to make your decision?
You can see from these photos how they thought of "steepness."
Question 3: Now discuss your ranking in #1 with another classmate. Are you going to change your ranking? If so, please indicate your new ranking.
Question 4: Now discuss your ranking in #3 with a different classmate. Are you going to change your ranking? If so, please indicate your new ranking.
Six students made no change to their original ranking after talking with two other classmates, 16 made one change, and 9 made two changes.
I was already so happy to see how the activity was coming along. I didn't realize how much more I was about to learn from Question 5 and beyond.
Question 5: You may now measure the staircases with whatever tool(s) you need. Use the space below to keep track of your measurements, calculations, and notes.
A few kids asked for a protractor, most used a ruler. Most of those who used a ruler measured this length.
Me: Now that you have these measured, what do the numbers mean
Matthew: (Silent, mumbling...)
Me, pointing to staircase F: I see this has the longest length. Was this your steepest shape?
Matthew: Oh no. D was the steepest.
Me: Okay. Shape C has the shortest length. What does that mean in terms of steepness?
Matthew: I don't think these numbers are right.
I went over to Troi's desk, she too had measured the same lengths as Matthew did.
Troi: These numbers didn't do anything for me.
Me: What makes you say that?
Troi: Well, the staircases are all different sizes, you'd have to make them all the same to compare them.
She then measured the rise of each step. I left her to do so.
Rapha: I'm measuring the height, but it depends on the width too.
She didn't do any more with the two sets of numbers.
Zoe: Can you show me how to use a protractor?
Me: Sure. Which angle do you want to measure?
She pointed to the middle of the staircase. I worked with her for a little while.
I checked on a small group of boys who seemed to be using the protractors correctly.
Mike: We agree on the rest of the ranking. We're just not sure about B and E. They're like one degree apart.
Ryan, holding up two different brands of protractors: These aren't even measuring the same.
Me: Hmmm. Tools aren't perfect, are they?
I was watching the time; we had 20 minutes left of our 2-period class. I asked them for a "final answer" after whatever measurements they'd done, "Put this ranking at the bottom of your worksheet."
By then the kids who used a ruler had abandoned the tool for the protractor. Make no mistake, these kids were pretty confident that if Ryan and Mike were measuring the angles, then they ought to be doing the same. More importantly, they noticed that the angle measurements correlated with their steepness rankings.
I asked Miles first — just because he sat front row, right side — for his ranking: D A B E C F. I asked if anyone else had the exact same as Miles'. Twenty hands went up. I asked for Moses' ranking: D A E B C F. Ten hands went up for this ranking. That only left Sierra with a different ranking. (Sierra was one of six who never changed her original decision.) Because B and E do have the same steepness, all 30 of 31 kids were correct.
Now what? Somehow ending the lesson here seemed weird, even though we had a lot of good conversations. They used angles to figure out steepness. I hadn't planned this! What about the ruler?!
So I said, What if you didn't have a protractor? What if you only had a ruler? What would you measure instead?
I then defined lengths on the staircase that could be measured with a ruler so we could all speak the same language about what was measured.
I said, It was great that you figured out steepness using a protractor. But now I want you to figure out how to find steepness using a ruler. Which of these lengths would you measure? Do you need to measure more than one? And if you measured more than one, what would you do with the two/three numbers you have?
They began measuring ferociously, calculators in hands. (Yes, we use calculators all the time!) I didn't see anyone measuring the slant. I got this much from them by walking around and asking:
Base minus height.
Base divided by height.
Base times height.
Height divided by base.
I ended with, For homework, please finish measuring and calculating for all six staircases. Do your calculations support the ranking?
Troi walked up to my desk when most students had already left, Can I change? I already knew... I did base times height. That didn't work.
#peedinmypantshappy
Always Sometimes Never
I did Always-Sometimes-Never (ASN) questions with my 6th graders. The kids were randomly paired up to work on placing 18 mathematical statements into the appropriate columns: always true, sometimes true, and never true.
The students were involved in the discussion and coming up with examples. They had to translate some statements into equations or inequalities and defend their answers. They learned to give counterexamples.
ASN works for any math level (and could be used in other subjects). The kids are comfortable working and having that math conversation with just one other person initially; then, they build up the confidence to share their reasoning with the whole group later.
I got this particular set of 18 from Swan and Ridgway. Sixth Sense has a set also.
Here are the statements we used:
Max gets a pay raise of 30%. Jim gets a pay raise of 25%. So Max gets the bigger pay raise.
When you cut a piece off a shape, you reduce its area and perimeter.
If you add the same number to the top and bottom of a fraction, the fraction gets bigger in value.
In a sale, every price was reduced by 25%. After the sale, every price was increased by 25%. So the prices went back to where they started.
(a+b)/2 ≥ sq(ab)
If you divide the top and bottom of a fraction by the same number, the fraction gets smaller in value.
It doesn't matter which way you multiply; you get the same answer, like 𝑎 × 𝑏 = 𝑏 × 𝑎.
If you add a number to 12, you get a number greater than 12.
The square root of a number is less than the number.
It doesn't matter which way you divide; you get the same answer, like a ÷ b = b ÷ a.
If you divide 12 by a number, the answer will be less than 12.
The square of a number is greater than the number.
p + 12 = s + 12
n + 5 < 20
2(x+3) = 2x + 3
3 + 2y = 5y
4p > 9 + p
2(3+s) = 6 + 2s