Two Pizzas and Five People

I'm thinking a lot about how my 6th graders responded to a pre-lesson task in "Interpreting Multiplication and Division" — a lesson from Mathematics Assessment Project (MAP) .

MAP lessons begin with a set structure:

Before the lesson, students work individually on a task designed to reveal their current levels of understanding. You review their scripts and write questions to help them improve their work.

I gave the students this pre-lesson task for homework, and 57 students completed the task.

I'm sharing students' responses to question 2 (of 4) only because there's already a lot here to process. I'm grouping the kids' calculations and answers based on their diagrams.

Each pizza is cut into fifths.

About 44% (25/57) of the kids split the pizzas into fifths. I think I would have done the same, and my hand-drawn fifths would only be slightly less sloppy than theirs. The answer of 2 must mean 2 slices, and that makes sense when we see 10 slices total. The answer 10 might be a reflection of the completed example in the first row. "P divided by 5 x 2 or 5 divided by P x 2" suggests that division is commutative, and P here must mean pizza.

Each pizza is cut into eighths.

Next to cutting a circle into fourths, cutting into eighths is pretty easy and straightforward.

Each pizza is cut into tenths.

I'm a little bit surprised to see tenths because it's tedious to sketch them in, but then ten is a nice round number. The answer 20, like before, might be a mimic of the completed example in the first row.

Each pizza is cut into fourths.

I'm thinking the student sketched the diagram to illustrate that the pizzas get cut into some number of pieces — the fourths are out of convenience.  The larger number 5 divided by the smaller number 2 is not surprising.

Each pizza is cut into sixths.

It's easier to divide a circle by hand into even sections, even though the calculations do not show 6 or 12.

Each pizza is cut into fifths, vertically.

Oy. I need to introduce these 3 students to rectangular pizzas. :)

Five people? Here, five slices.

Mom and Dad are bigger people, so they should get the larger slices. This seems fair. We just need to examine the commutative property more closely.

 Circles drawn, but uncut.

I'm wondering about the calculation of 5 divided by 2.

Only one pizza drawn, cut into fifths.

9

Twenty percent fits with the diagram, if each person is getting one of the five slices. The 100 in the calculation might be due to the student thinking about percentage.

Only one pizza drawn, cut into tenths, but like this.

10

I wonder if the student has forgotten what the question is asking for because his/her focus has now shifted to the diagram.

 Each rectangular pizza is cut into fifths.

Three kids after my own heart.

Five portions set out, each with pizza sticks.

I wonder where the 10 comes from in his calculation.

Five plates set out, each plate with pizza slices.

Kids don't always know what we mean by "draw a picture" or "sketch a diagram." This student has already portioned out the slices.

What diagrams and calculations would you expect to see for question 3?

There's important work ahead for us. The kids have been working on matching calculation, diagram, and problem cards. They're thinking and talking to one another. I have a lot of questions to ask them, and hopefully they'll come up with questions of their own as they try to make sense of it all. If I were just looking for the answer of 2/5 or 0.4, then only 12 of the 57 papers had this answer. But I saw more "correct" answers that may not necessarily match the key. We starve ourselves of kids' thinking and reasoning if we only give multiple-choice tests or seek only for the answer.

That's why Max Ray wants to remind us of why 2 > 4.

A Lesson Salvaged

The intended activity from MAP did not go well last week.

I gave these instructions:

1. Pair up. One person is the Describer, the other the Drawer.

2. The Describer is going to look at a Roman mosaic and describe it to the Drawer to draw it.

3. Both people may talk to each other, but no hands or any other bodily gestures.

4. The Describer may not look at the Drawer's paper as he/she works on the drawing.

I gave each Drawer a blank sheet of paper. I gave each student a ruler and a compass. And I gave each Describer a picture of this.

I also told the Describers to get their Drawers to get the size just right — thus the ruler. I encouraged the Describers to use words like rotate, reflect, symmetry. After a while, I walked around looking at the papers and thought, Holy Cow, if-only-you-could-see-what-your-drawer-is-drawing.

I called for the Drawers' papers after about 30 minutes. The results:

What the...? Oh, let's not forget No. 7. Sketches 4 and 7 took up most of the 21.5 cm x 28 cm paper; the actual mosaic was 8 centimeters in diameter.

Then, I thought, Let me try being the Describer!

The results

Sketch D was very close, considering we were all hurrying through as the period was ending. Still, this was not my assignment and not a fair comparison when I had a lot more time to look at the shape. I took the stack home and let it mingle with the other piles of papers on my desk.

Late last night I looked again at the sketches on my desk and thought, I should try to construct this shape in Geometer's Sketchpad (GSP).

It was not an easy task!! I had to really think about each step and kept wondering during my construction if there was a better or more efficient way to do this. I felt great when I was done because it was challenging. No reason to keep this experience to myself, so I asked my geometry kids this morning to construct the Roman mosaic in GSP!

I reminded them that their constructions must pass the "drag test," meaning their Roman mosaic must not collapse when any vertex got dragged about.

Five minutes into the construction, Bobby said, "This makes me crazy!" Yes!

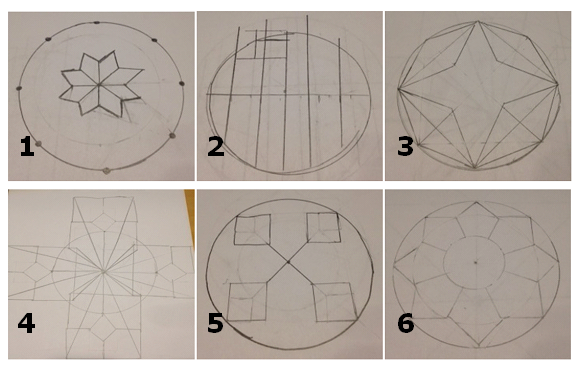
Some works in progress:

Karie was one of the first ones to finish; she talked about her construction:

Alex talked about his construction. You could hear the dismissal bell while he was talking, but no one got up to leave or put away the laptops. I had to tell them!

It was cool that the five students who had finished all had different ways of constructing the mosaic. Theirs were much more elegant than mine. More importantly, my construction did NOT even pass the drag test when I tried it this morning, but I intentionally forgot to tell them this.

A lesson salvaged by GSP. A teacher schooled by her 8th graders.