My Other Math Sites
Lessons From the Classroom
Desmos Puppy House
We don't cover quadratic in Math 8 this year, so we really can't do Des-man. I come up with "Puppy House" instead so my students can still create something that allows them lots of practice with writing linear equations with domain and range restrictions.
They draft the house on paper. The house needs to have a minimum of 6 slanted lines, 5 vertical lines, 5 horizontal lines, and one image of a puppy at entrance of house.
Below are the ones from my Math 8 Honors kids who learned quadratic last year. They completed these within one 55-minute period. So proud of Ashlynn for remembering how to write inequalities.
Andrew
Ashlynn
I'd love to see what amazing dog houses your students will create. (Someone create a flap door for me to play peek-a-boo with the puppy please!)
Teaching Absolute Value
I know Common Core does not have absolute value in grade 8, but I'm teaching it anyway because we're still doing "algebra 1" this year. (A year ago Raymond Johnson looked into the inclusion of this topic in the different grade levels.) My 8th graders know that the absolute value of 5 is 5, and the absolute value of -5 is also 5. Some recall that it's the distance from 0 on the number line. We begin by solving a few of these: abs(x) = 4, abs(a) = 0, abs(w) = -3. A few trip up on the last one but recover quickly and move along.
Me: What is the distance between these two points?
Class: Eight.
M: How did you get eight?
C: Subtract.
M: What about this one? The points are at -3 and 9.
C: The distance is twelve.
M: This one?
C: Thirty-two.
M: Good. Distance is always positive... How did you find the distance between the points again? What operation did you use?
C: Subtraction!
M: Then I'm going to add an equation below each number line showing subtraction. Is that okay?
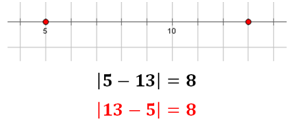
M: So, the distance between 5 and 13 is 8. Then, what is the distance between 13 and 5?
C: Eight
M: Woah! It's the same? Meaning I can write the equation either way?
Kids agree that subtraction can be commutative when it's inside the absolute value bars because we’re just measuring distance. The distance from Johnny to Julie is the same distance as from Julie to Johnny. I'm not going to argue.
Me: Given two points, you can tell me the distance between them. So now I’m going to give you just one of the two points but tell you the distance between them, and you find the missing point x.
C: x is ten.
M: Yea, ten works. Let's try to read this open sentence. How would you say it?
C: x minus six... The absolute value of x minus six is four.
M: Hmmm. Oh, you say the words 'absolute value' because they're there. Let's try again without saying those words. Use the word 'distance' instead.
C: The distance of x minus six equals four.
M: Let me show you again the first one that I'd asked you. I remember just asking you, 'What is the distance between 5 and 13?' What did I not say even though it's there?
C: Minus.
M: Right. Let's not add stuff we don't need. You know naturally that finding distance implies subtraction. So, say the equation again.
C: The distance between x and six is four.
M: Or you could say...? Can we switch the points around?
C: The distance between six and some point x is four.
M: Alright. Is 10 the only answer for x? We are trying to find a point on the line that makes the equation true. So, let's use the number line to solve this. Because we know 6 is one of the points, let's locate it. We need to find the other point that would be a distance of 4 away from 6. So, it could be to the right of 6, or to the left of 6. Where does this put us at?
M: Oh, why isn't the point -6? I see a 'minus six' in the equation.
C: Remember, that minus is for subtracting. We need it there to find distance.
M: I remember. We need it.
We do a few more of these. Enough to bore us, need something new.
M: Let's try this.
C: No subtraction sign.
M: And you said we needed it. Then create it. Make it happen without changing the problem of course.
C: Change it to minus minus...
M: What does this problem say now?
C: The distance between x and negative eight equals five.
We do a few more of these. Enough to bore us, need something new again.
M: What about this?
M: Nothing terribly exciting. The other point(s) that we find is now worth 2x, so we just need to solve for x.
Then we do a batch of these:
Hey, what about these, where there's more stuff stuck around the absolute value quantity. Oh, we just need to first isolate the absolute value, then it's business as usual.
We spend the next whole class using Desmos to explore the shifts/changes to the parent absolute value function. Students need to write down their predictions first before graphing. One student was very excited when she got the V-shape to turn upside down.We discuss some real-life scenarios that may involve absolute values: margins of error, ranges of measurements: distances, scores, speed, temperatures, pH levels, elevations, etc.
Not proud to admit that I spent a lot of hours in college playing pool instead of studying, but never once did I associate the path of the ball as an absolute value function. Consider me odd if I always thought of angles instead.
Solving absolute value inequalities start similarly enough. Kids know from graphing inequalities that there's "shading" involved. They also know the difference between open and closed points. So I just have the kids use their thumb and forefinger to indicate the distance between the two points, then if the inequality says less than [or equal to], then it's natural to pinch their fingers closer together, indicating that the region inside the points need to be shaded.
The textbook will tell kids to set up the "two cases" to solve these inequalities (same thing with equations).
Then, kids are asked to graph the solution. But if kids learned to solve using the number line itself, then there would be nothing to memorize because they learned distance way back when they started learning to crawl. And since the graph shows the solution, then writing what that solution is is easy because it matches the graph. Like below, x lives on the green line between -8 and -2, being ≥ -8 and ≤ -2.
For greater than inequalities, the student would naturally spread his fingers apart to indicate shading outside of the points.
I don't know why there seems to be a lot of rules when learning to solve absolute value equations — which inequality sign for when it's and or when it's or.
Vroom Vroom
I normally share a lesson that I've already done with students, but I'm still tweaking this one and needing to write some thoughts down before my noggin turns back into soft tofu. I bought these 14 pull-back friction toy cars (2 sets) for $30 at Costco. Amazon posts a video of how well these soft squeezable cars can stand up to toddler abuse.
On your mark...
Each team of 3 students gets 1 car.
How far the car moves forward depends on how far it gets pulled back — good lesson too for talking about potential and kinetic energy.
The challenge is to get your team's car to go a certain distance (reach finish line) without going over. This distance is not revealed until later.
To predict for how much pull-back a car needs to go a certain distance, students "test drive" their cars for pull-backs of 2, 4, 6, and 8 inches.
Get set...
Students are instructed to take measurements from the car's front wheels.
The blue tape marks the starting line. Front wheels line up at the front of the tape.
The car is then pulled back a certain distance — here it's 2 inches — and let go.
When the car stops, the distance traveled is measured from front of wheels to front of blue tape. Looks about 13.2 inches here.
Go!
Teams do 3 trial runs.
Record and graph data on Desmos.
Now teacher reveals and marks the distance each car needs to travel without going over. Say 15 inches.
From graph, students extrapolate what the pull-back distance would need to be for car to move forward 15 inches. This distance is recorded and cannot be changed.
Teams line up with their cars — one at a time — to pull back and let go!
Winning car is one that reaches closest to finish line without front wheels going past it.
Considerations
The cars roll best on bare floors. My classroom is carpeted, so we'll need to do this outside.
It's fun that the cars actually vary in speed for same pull-back distance. The sports car (bottom left in above picture) is fastest.
My kitchen floor is not big enough to test longer than 8-inch pull-backs, but the graph appears more parabolic.
The data looks pretty awful, doesn't it? Kinda? Maybe?
Ginny from Mathalicious was in the kitchen when I was playing with these toy cars. She shook her head and wondered if empty nest syndrome got the best of me. No matter. I think this will be a lot of fun. Will report back and post some pics.
[Updated 12/01/13] Jon Orr did this lesson with his Grade 9 students and wrote a great summary on his blog.
Here are a few pics from my class:
And a couple of video clips:
Des-man
Not only was this so great to reinforce slope, y-intercept, and all the coefficients, it also allowed us to talk about domain and range.
What I heard around the room (that I can remember):
Oh, I get this now! I see what changing this number does!
Oops, I made his face too wide!
His smile is crooked. But I think I'll leave it because he looks cool that way.
Ha!! I see my mistake, I said x had to be greater than 4 but less than 2. Silly me.
I want the eyes to be oval shaped though. My plan is to make 2 parabolas opening into each other.
Can we work on this in 6th period too?
When I saw two students whose graphs were circles for faces, I knew they'd copied these from Desmos gallery as we haven't — and won't — learn circle equations in Algebra 1.
I reminded them of the minimum requirements, but I told the class that they may copy equations and tinker with them to add other features, such as hair and whiskers. (I actually said "whiskers," and Lexi had to tell me, "Whiskers? On a man? You mean beard or mustache?") People don't have whiskers? Good to know.
I made my guys' eyes elliptical and tweeted it, the good folks at Desmos responded.
So cool!
I think we got a lot of mileage from this activity. It's a good sign when teacher instruction is minimal and student engagement and discussion are high.
Just in case you missed the Grand Opening of Daily Desmos about 3 weeks ago, brought to us by Michael Fenton, inspired by Dan Anderson.